Asymptotic Gridshell

Type: Poster & Model

Year: 2016

Team: Denis Hitrec, Eike Schling

Office: Technische Universität München, Chair of Structural Design, Prof. Dr.-Ing. Rainer Barthel

Exhibition: Advances in Architectural Geometry 2016, ETH Zurich

 

Experimental Structures is a research studio held annually at the Chair of Structural Design, Technische Universität München. We are searching for methods to simplify the construction of double curved surfaces. Through physical and computational experiments we demonstrate new possibilities for an intelligent symbiosis of form, structure and fabrication.

 

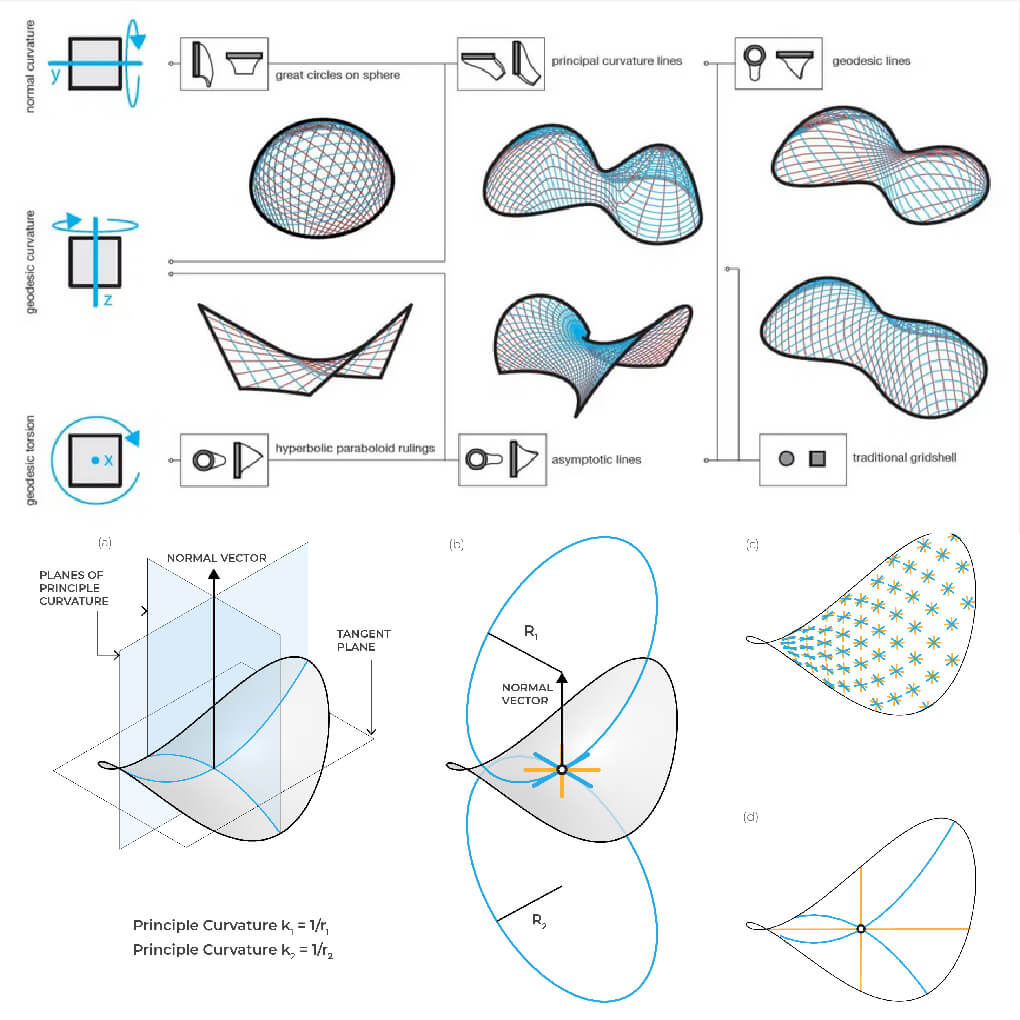
Curvature of Lines on Surfaces A line on a surface can have three types of curvature: normal curvature, geodesic curvature and geodesic torsion

 

Imagine an ant walking along a surface. To follow the implied line, the ant must either walk up or downhill to follow the normal curvature; it could turn left or right to follow the geodesic curvature; or it must turn around the axis of the line to be able to stand with its legs straight on the surface – this is called the geodesic torsion.

 

By omitting one of the three curvature types we can create specific line networks, which have decisive advantages for the construction of curved support structures. Figure 1 shows the different types of curvature (left) and their related curve networks. Indicated in the boxes are the bending or twisting of profiles, necessary to construct such networks.

 

At any point on an anticlastic surface there are two asymptotic directions. They are the direction of zero normal curvature. If we follow these directions, step by step, we can generate an asymptotic curve. This curve will only turn sideways (geodesic curvature), but never up or down (normal curvature).

 

Structural elements that run along asymptotic lines and are oriented orthogonally to the surface can be unrolled to become straight strips.

 

This is a decisive advantage for fabrication and material efficiency. Furthermore, on a minimal surface, these „asymptotic strips“ always intersect at 90 degrees. This allows for a simplified construction with rectangular joints.

 

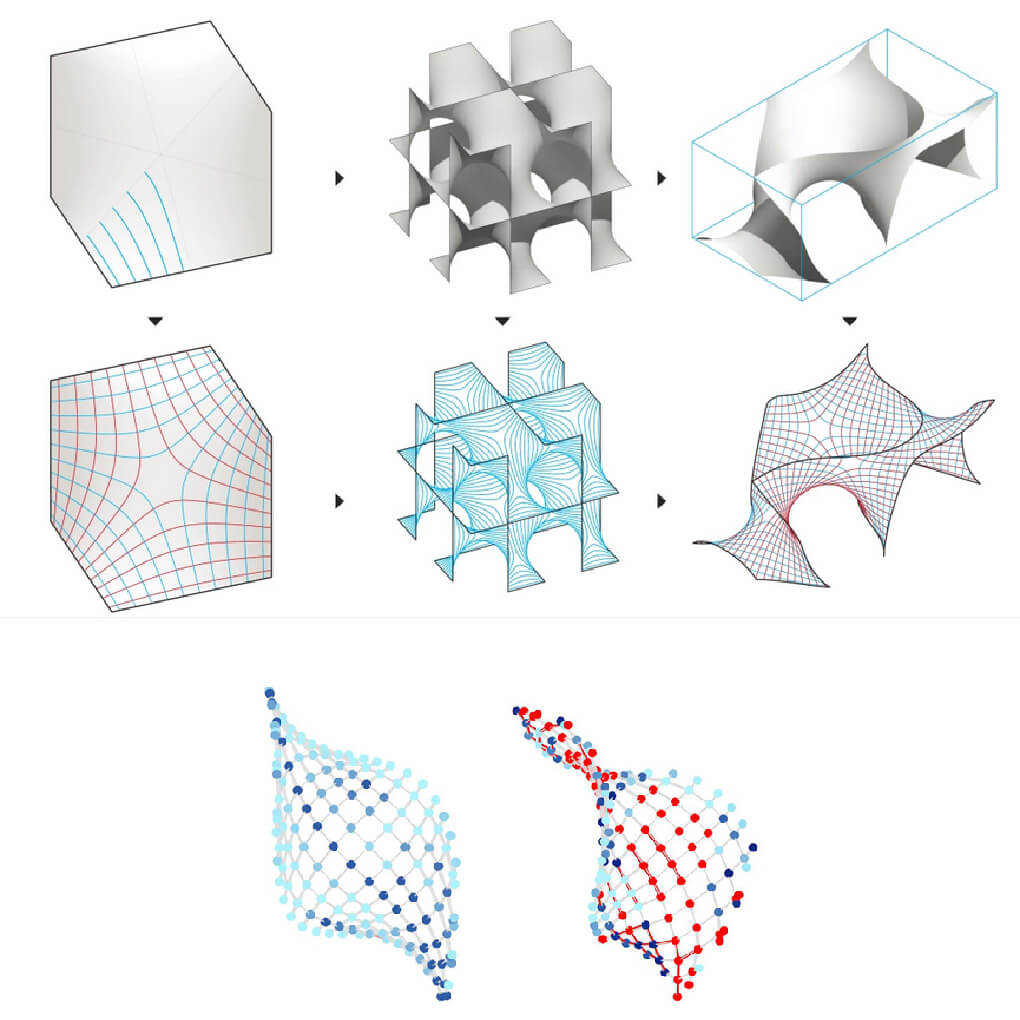
Design proposal of a pavilion for the Structural Membranes Conference 2017 in Munich.The design takes a clipping of a repetitive, cubic Schwarz D minimal surface, to generate an expressive sculptural space.The support structure follows a curve network of asymptotic lines. All elements can be constructed out of straight strips with orthogonal nodes. Future research will investigate material use, structural performance and assembly methods for this new type of gridshell.

 

Eight fundamental units complete the cubit unit cell of a Gyroid surface. Due to the scale of the proposal, I have introduced two layers of lamellas. This is to ensure each layer is sufficiently slender to be easily bent and twisted into its target geometry, whilst providing enough stiffness to resist buckling under compression loads.

 

Inspired by the highly symmetrical and optimised physical properties of a triply periodic minimal surface, ‘Minimal Matters’ aims to create an explorative, meditative and interactive experience for visitors. It is a strained grid shell utilising the geometrical benefits of an asymptotic curve network; digitally designed via algorithmic rules to minimise material, cost, and construction time.

 

References:

Link1 / Link2

Images:

Asymptotic Grid…/wordpress.com

Asymptotic…/eikeschling.com

Asymptotic Gridshell/researchgate.net