GALAPAGOS ON THE LOGIC AND LIMITATIONS OF GENERIC SOLVERS

David Rutten

^{Department of Architecture, University of TU Delf, Netherland}

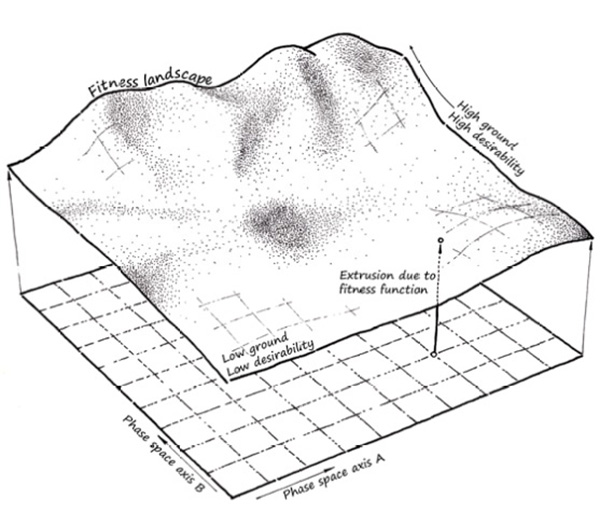
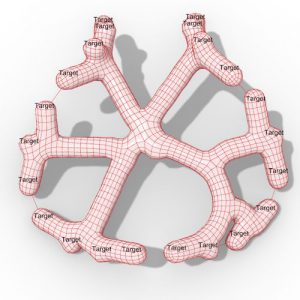
Phase spaces and their fi tness landscapes The relationship between a two-dimensional phase space and the resulting three-dimensional fi tness landscape.

Generic solvers, despite being called generic, can only be applied to a subset of all possible problems. To understand the limitations of a solver, one needs to understand both its underlying theory as well as the algorithmic representation of any given problem.

These must necessarily remain somewhat abstract as the dimensionality of a problem is dependent on the chosen formulation, which is often far beyond what mere humans can visualise. It is, however, possible to explain some of the topologies of phase spaces through vernacular language by treating only lowdimensional cases, which fall within the realm of the imaginable.

This article discusses the parallels between phase space topologies and computational terminology as well as how generic solvers arrive at their solutions.

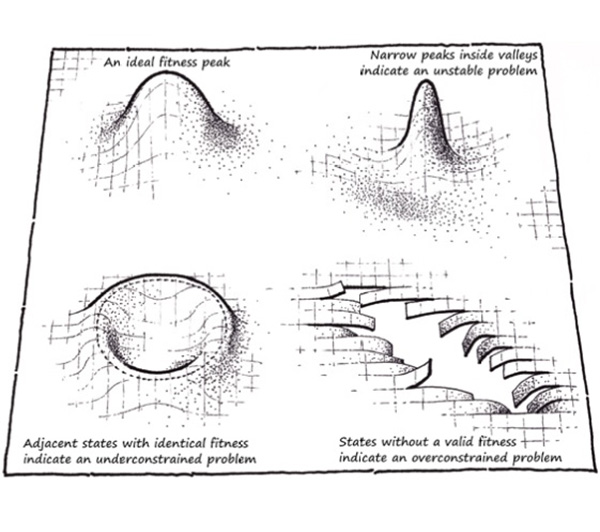
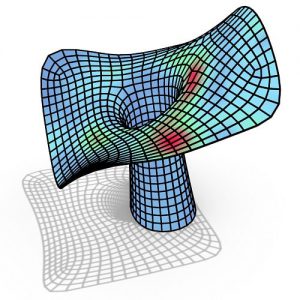
Common fi tness landscape topologies Specifi c classes of problems result in specifi c landscape topologies. Problematic topologies can usually be repaired by adjusting the fi tness function.

Problems come in many shapes and sizes. Some have an obvious solution, some have no possible solution, and some solve themselves if only we stop picking at them. There are well-defined mathematical classes of problems that categorise solvability: NL, NP-Hard, NP-Complete.

Although these categories are of interest to complexity theorists, they are well beyond what the average person can make use of. Here, I will use the metaphor of landscape to explain the search for possible solutions. We are all familiar with the basic geometry of landscapes, which thus provides a good locus for a shared narrative.

So what exactly do we mean by ‘problem’ and ‘solution’? A fairly hardcore definition of both would be that a problem is the extrusion of a system phase space, and a solution equals high ground in this newly created landscape. This sentence probably contains more unknowns than most are comfortable with, but I will do my very best to explain.

You may have heard the term ‘phase space’ before, perhaps even from someone who was trying to impress you. Mathematicians love to use 10-dollar words for two-cent notions, and this is no exception. A phase space is nothing more than the collection of all possible manifestations (states) of a given system.

For example, let us imagine the system of a hanging chain. If the end points are fixed, then the only variable is the chain length. A system with a single variable is represented by a phase space with a single dimension. In one phase space corner we find short chains, and in the other, long chains.

But if we allow the suspension points to move freely across the ceiling, the number of variables increases to five. Each suspension point can move in the X and Y directions, and of course the chain length also remains a variable.

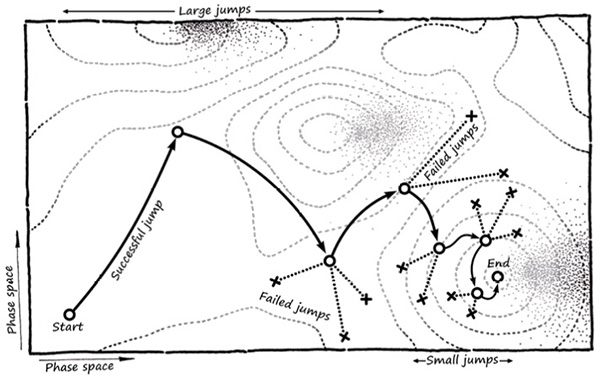
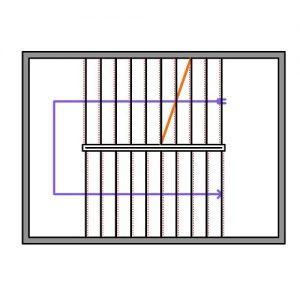
Schematic representation of a simulated annealing run The progression of an annealing solver can be represented as a series of converging jumps.

The phase space for this new system is a five-dimensional volume, which is not something you can imagine, nor is it something I can draw on a piece of paper. There is no theoretical upper limit to the dimensionality of a phase space, and complicated problems can easily have thousands upon thousands of variables.

There is no guarantee that a solver will find the best solution in a finite amount of time. There could not be. The best we can hope for is a solution of acceptable quality in an acceptable amount of time. How well a solver performs (how many iterations it takes to find an acceptable solution) depends largely on the topology of the fitness landscape.

Large horizontal plateaus tend to confuse a solver as it is not obvious in what direction it is smart to move. Areas that slope away from high peaks will give wrong directions, so to speak. Landscapes with gaps can trap solvers by restricting their movement.

Rough or, worse, fractal terrain is bad as it scatters the solver momentum. The topology of the landscape is a direct result of the fitness function and is therefore at the mercy of whoever defined the said function.

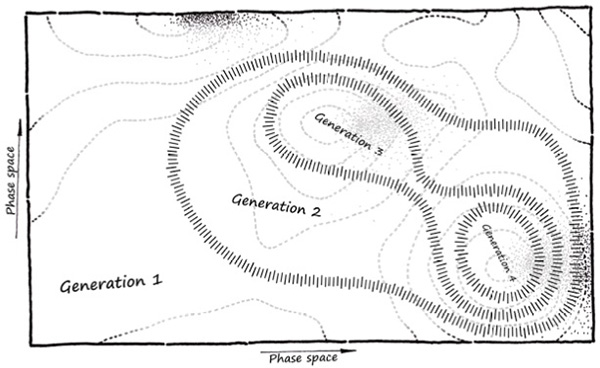
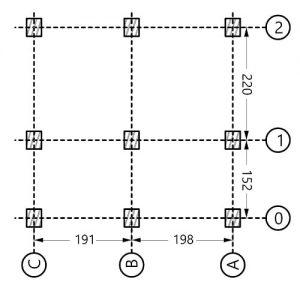
Schematic representation of an evolutionary solver run The progression of an evolutionary solver can be represented as a series of contracting boundaries that delineate the evolving population.

I would like to explain two very different generic solver classes, both of which I implemented in the Galapagos plug-in for Grasshopper®. This will necessarily be a very brief explanation that cuts many corners, but the basic idea behind each solver is not very complicated. Both are based on real-life processes: one physical, one biological.

Simulated annealing applies the theory of thermodynamics to search algorithms. More specifically, the process of crystalline matrix formation that occurs when molten metal is allowed to cool. When the atoms cool down, they start banding together into tiny crystals that grow larger as the temperature drops.

This process can be described by a set of equations, which can in turn be employed to find peaks in a landscape. The way an annealing solver progresses is by jumping randomly across the landscape in ever decreasing steps. If it does not accept the new location, perhaps because it is worse than before, it will revert to the previous one.

Evolutionary algorithms apply the biological principles of mutation, selection and inheritance. They will populate the landscape with virtual individuals and then proceed to breed the highest ones in the hope that their offspring will be closer to a summit. Much decision-making is involved here regarding mate selection and various stochastic processes, but these are mere details.