Origami & Kirigami
In anticipation of the exhibition 40 under 40: Craft Futures, on view at the Renwick Gallery of the Smithsonian American Art Museum from July 20, 2012 — February 3, 2013, the museum asked the 40 artists featured to share personal videos of themselves with our audience. Here’s what Erik Demaine submitted.

Origami is the ancient Japanese art of paper folding. One uncut square of paper can, in the hands of an origami artist, be folded into a bird, a frog, a sailboat, or a Japanese samurai helmet beetle. Origami can be extraordinarily complicated and intricate.
The art of origami has been going through a renaissance over the past 30 years, with new designs being created at ever-increasing levels of complexity. It’s no coincidence that this rise in origami complexity has emerged at the same time scientists, mathematicians and origami artists themselves have been discovering more and more of the mathematical rules that govern how paper folding works.

Indeed, if you take an origami model, of a bird for example, and carefully unfold it, you’ll see the pattern of creases that act as a blueprint for the model. This crease pattern contains the secret of how the paper is able to fold into the bird – and that secret is math. In theory, we could use this crease pattern to determine exactly how the paper should fold up and what shape it will form – if, that is, we understood all the secret rules of paper folding.
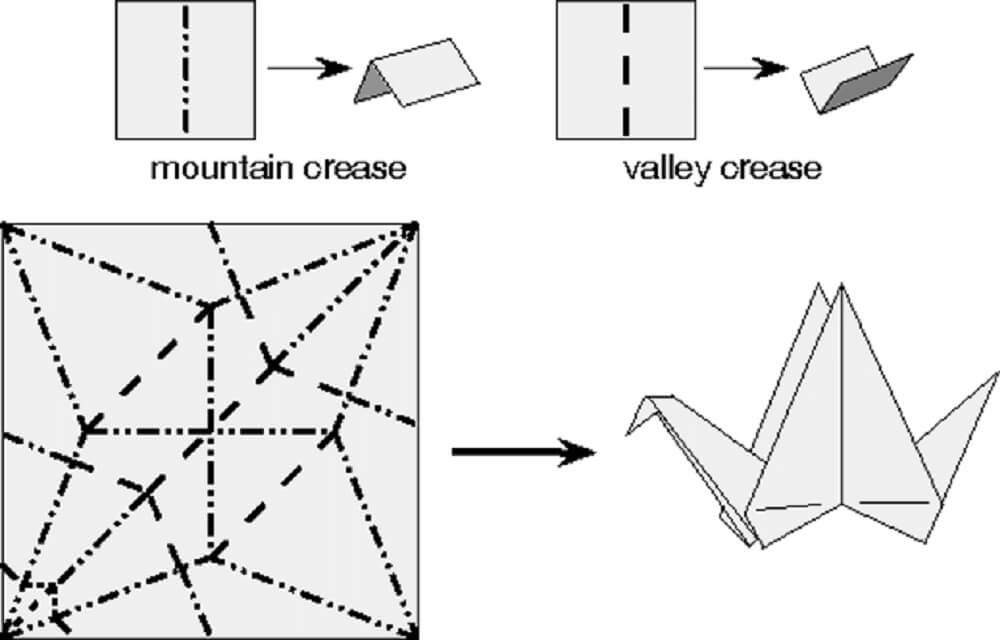
At heart, mathematics is about understanding the rules and patterns of the universe, be they patterns in numbers, in the stock market, or in nature. In the case of origami, we need to look at the geometry of the crease pattern, where the lines intersect, what angles they form, and in what direction the creases fold: are they valley creases or mountain creases?

Most traditional origami models fold flat, meaning you could press the model in a book without crumpling it. It turns out that the crease patterns of flat origami models have some very special properties. One of them is called Maekawa’s Theorem: at every vertex where creases intersect in a flat origami crease pattern, the difference between the number of mountain and valley creases is always two. So, at a vertex you could have 5 mountains and 3 valleys, but never 6 mountains and 2 valleys, for example.




Comments