Shortest Path on Mesh
In this grasshopper example file by defining a series of points you can create a pattern on a mesh based on the shortest path between two points.
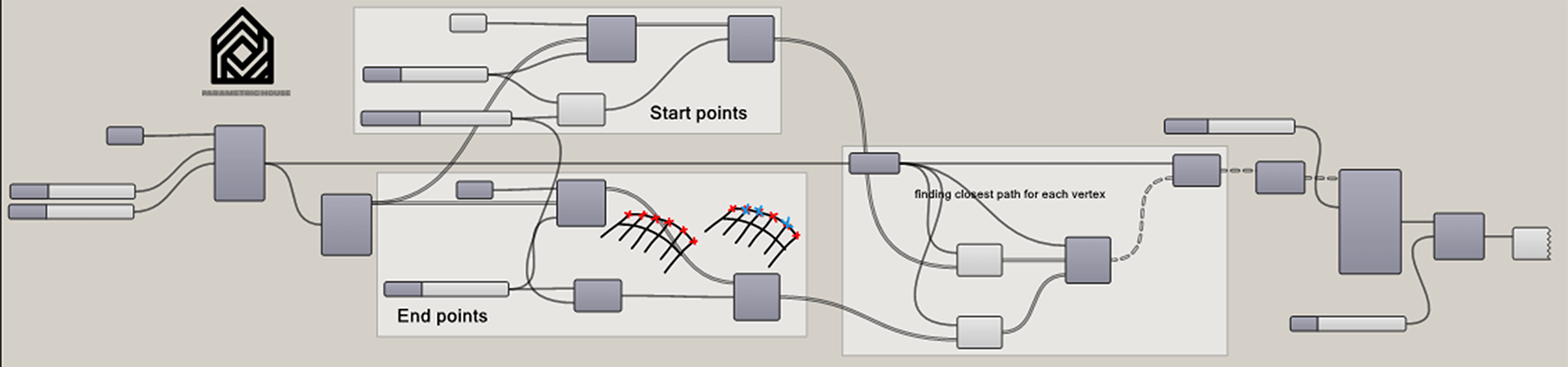
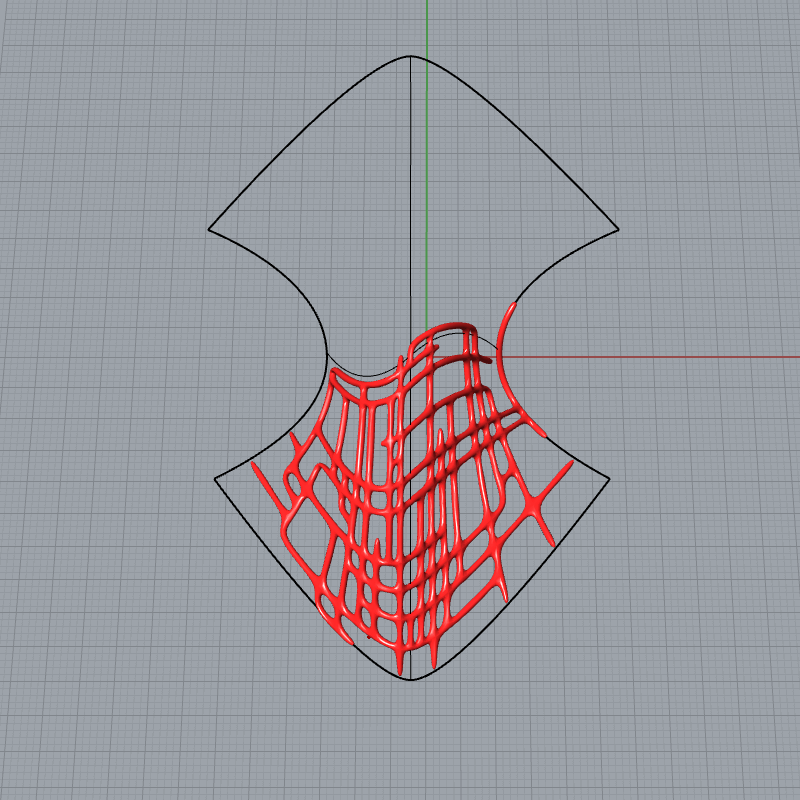
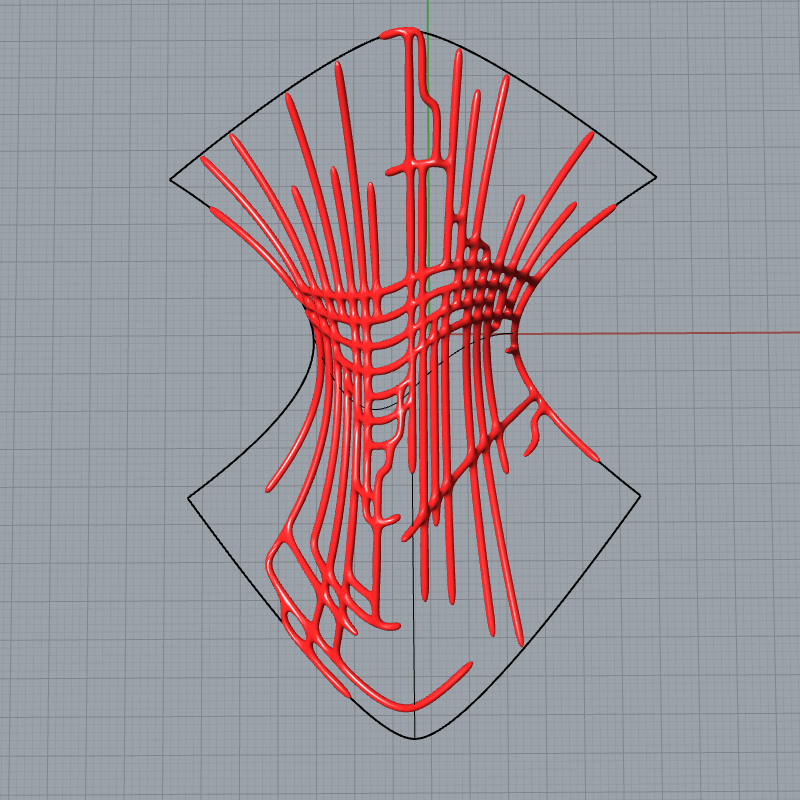
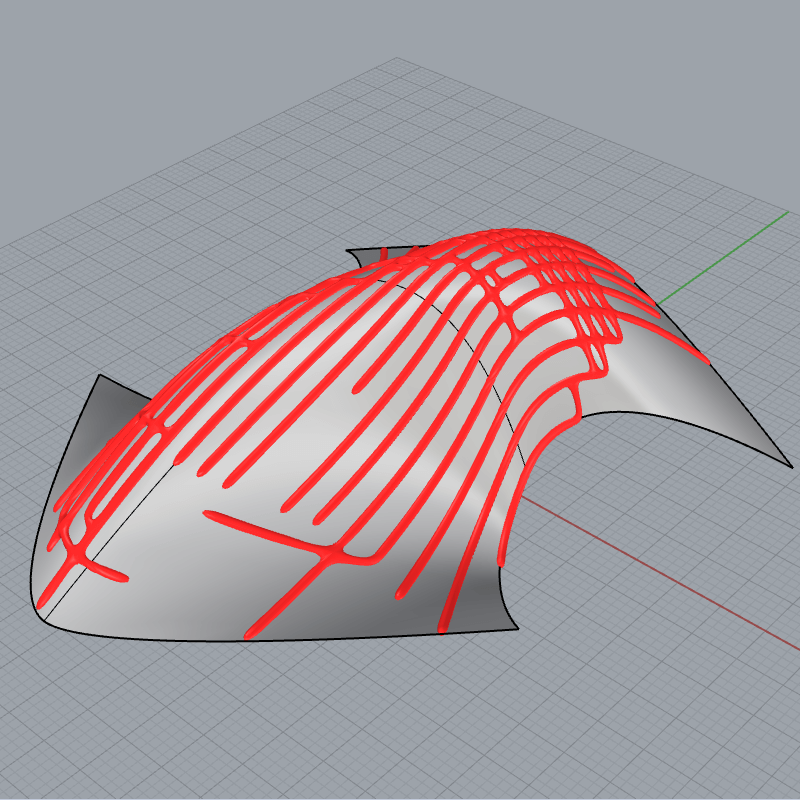
In this Grasshopper example file, You can carve a field based pattern on a mesh using the Nursery and Dendro plugins.
In this Grasshopper example file, You can simulate a series of particles on a Nurbs Surface using the Nuclei plugin.
In this Grasshopper Topos example file, you can optimize the structure of a bridge by using the Topos plugin.
In this Grasshopper example file, you can design a waffle table by using the Bowerbird plugin.
In this grasshopper example file, you can design a parametric ngl System by using the Weaverbird , Dendro and Rabbit plugins.
In this gasshopper example file, you can design a bridge similar to the Margaret Hunt Hill Bridge by Santiago Calatrava using the native components.
In this Grasshopper Example File, you can design a parametric deployable Bridge By using the Anemone Plugin
In this grasshopper example file, you can design a parametric reciprocal frame by using the ngon Plugin.
In this grasshopper ngon example file, you can design parametric hexagram bricks by using the HexDivide component from the ngon plugin.
In this grasshopper kangaroo example file, you can simulate an elastic material by using the Kangaroo anchor component.
In this grasshopper example file, you can design a parametric bridge by using the 3D Graphic Statics plugin.
In this Grasshopper example file, You can model a simple parametric pavilion using the TPS plugin.
In this Grasshopper example file, you can create a lattice pattern on a dress by using the Axolotl plugin.
In this grasshopper example file, you can design a Gyroid pattern by using the Millipede, Pufferfish and Weaverbird plugins.
In this Grasshopper example file, you can design a building similar to the Lisbon Orient Station by Santiago Calatrava by using the Clipper plugin.
In this Grasshopper example file, you can model a Parametric dome base on a star pattern using the Spider plugin.
In this Grasshopper example file, You can deform a mesh with an attractor using the Pufferfish plugin.
In this grasshopper example file, you use the Peacock plugin combined with Pufferfish to design parameteric Jewelry.
In this Grasshopper script, you can design a parametric Voxelized Table by using the Sasquatch plugin.
In this Grasshopper example file, you can simulate a differential growth pattern on a curve by using the sphere collide component from the Kangaroo plugin .
In this Grasshopper example file, you can simulate a structure using chain simulations from the Spider plugin.
In this Grasshopper example file, you can create a field and then project it on a Nurbs surface.
In this Grasshopper script, you can use the Fennec plugin combined with the Pufferfish plugin to unroll a polysurface.
Comments
Cfeldman
I would like “the result obtained” to be even a little more faithful to the original surface, how can I control that? I like this example to work on a model, but to make it more faithful to the original surface, should I implement that? I have tried to move the points, place them in the center of the surface … but still, the result seems quite randomized, and sometimes I even lose a part of the original surface, or part of it is not covered by the new tuveria. Could you help me to solve this? Thank you.
Cfeldman
for example, in the recent Curve Growth Tutorial …. one can perfectly recognize the surface sphere of origin, since the curve grew to define the sphere by means of the created pipe, …. but here, …. Although there is an original surface, the pipe created sometimes does not cover or redefine the created surface “100%”, but only in part, due to the position of the points? …. o How to adapt this exercise to recognize 100% the original shape?. [for example, I use this definition, to create a new green skin, for a Formal “Base” architecture …… ok …. but I would need the new covering skin to cover 100% of the base shape and not just a random portion of it. So how to do it? —I can send images from my pc, of this, but not from where I am now —-. Greetings & Help pls