Auxetic Materials
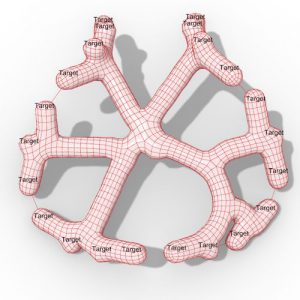
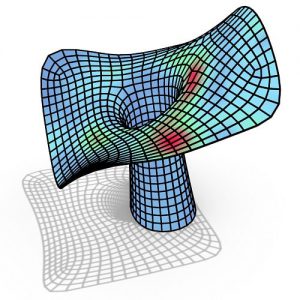
IGGRAPH 2016 Technical Paper by Mina Konakovic, Keenan Crane, Bailin Deng, Sofien Bouaziz, Daniel Piker, Mark Pauly. We present a computational method for interactive 3D design and rationalization of surfaces via auxetic materials, i.e., flat flexible material that can stretch uniformly up to a certain extent. A key motivation for studying such material is that one can approximate doubly-curved surfaces (such as the sphere) using only flat pieces, making it attractive for fabrication. We physically realize surfaces by introducing cuts into approximately inextensible material such as sheet metal, plastic, or leather. The cutting pattern is modeled as a regular triangular linkage that yields hexagonal openings of spatially-varying radius when stretched. In the same way that isometry is fundamental to modeling developable surfaces, we leverage conformal geometry to understand auxetic design. In particular, we compute a global conformal map with bounded scale factor to initialize an otherwise intractable non-linear optimization. We demonstrate that this global approach can handle non-trivial topology and non-local dependencies inherent in auxetic material. Design studies and physical prototypes are used to illustrate a wide range of possible applications.
Learn more at 👇
http://lgg.epfl.ch/publications/2016/…
























Comments