Mathematical Surfaces

In this video by Cutoutfoldup you can learn to make mathematical surfaces using bubble solution and wire.

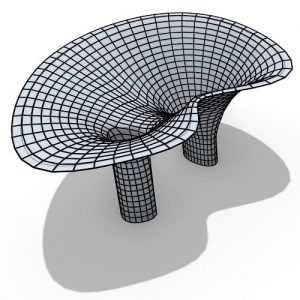
In mathematics, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solids; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space. Topological surfaces are sometimes equipped with additional information, such as a Riemannian metric or a complex structure, that connects them to other disciplines within mathematics, such as differential geometry and complex analysis. The various mathematical notions of surface can be used to model surfaces in the physical world.

In mathematics, a surface is a geometrical shape that resembles a deformed plane. The most familiar examples arise as boundaries of solid objects in ordinary three-dimensional Euclidean space R3, such as spheres. The exact definition of a surface may depend on the context. Typically, in algebraic geometry, a surface may cross itself (and may have other singularities), while, in topology and differential geometry, it may not.

A surface is a two-dimensional space; this means that a moving point on a surface may move in two directions (it has two degrees of freedom). In other words, around almost every point, there is a coordinate patch on which a two-dimensional coordinate system is defined. For example, the surface of the Earth resembles (ideally) a two-dimensional sphere, and latitude and longitude provide two-dimensional coordinates on it (except at the poles and along the 180th meridian). The concept of surface is widely used in physics, engineering, computer graphics, and many other disciplines, primarily in representing the surfaces of physical objects. For example, in analyzing the aerodynamic properties of an airplane, the central consideration is the flow of air along its surface.

A (topological) surface is a topological space in which every point has an open neighbourhood homeomorphic to some open subset of the Euclidean plane E2. Such a neighborhood, together with the corresponding homeomorphism, is known as a (coordinate) chart. It is through this chart that the neighborhood inherits the standard coordinates on the Euclidean plane. These coordinates are known as local coordinates and these homeomorphisms lead us to describe surfaces as being locally Euclidean.

In most writings on the subject, it is often assumed, explicitly or implicitly, that as a topological space a surface is also nonempty, second-countable, and Hausdorff. It is also often assumed that the surfaces under consideration are connected.

A closed surface is a surface that is compact and without boundary. Examples are spaces like the sphere, the torus and the Klein bottle. Examples of non-closed surfaces are: an open disk, which is a sphere with a puncture; a cylinder, which is a sphere with two punctures; and the Möbius strip. As with any closed manifold, a surface embedded in Euclidean space that is closed with respect to the inherited Euclidean topology is not necessarily a closed surface.