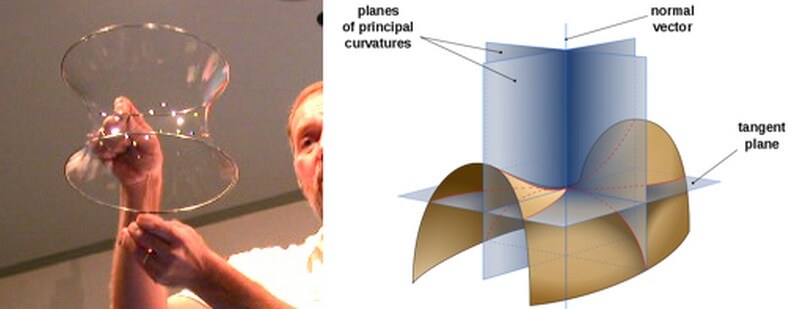
A minimal surface is a surface that is locally area minimizing, that is a small piece has the smallest possible area for spanning the boundary of that piece. Minimal surface also has zero mean curvature, which means the sum of principle curvatures at each point is zero. The shape taken by soap bubble is minimal surface .

The catenoid, the surface of revolution of a catenary, is a simple example.  Since 19th century when the bubble experiment was executed by a Belgium Physicist J. Plateau, more and more researches about minimal surfaces has been done by mathematicians and numerous type of surface has been discovered.

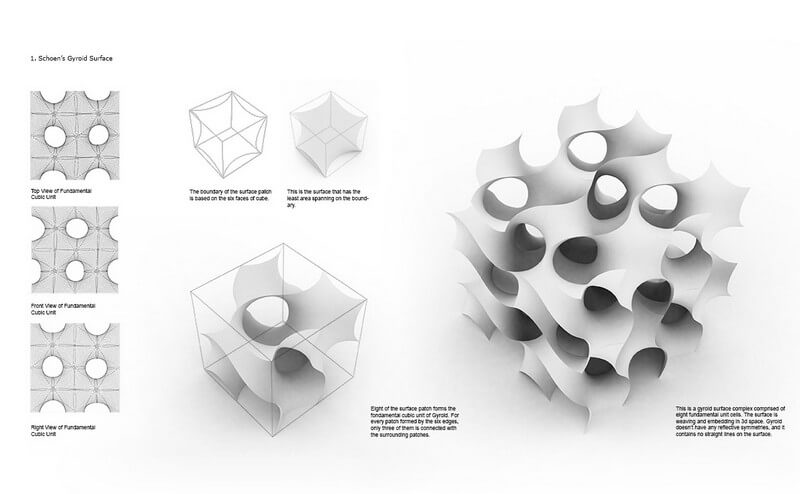
Among this minimal surfaces there is one type which is extremely fascinating, that is triply periodic minimal surfaces (TPMS) (no self-intersection). A TPMS can repeat themselves in three dimensions by rotating, mirroring and replicating. It is infinitely extending, has one of the crystallographic space groups as its symmetry group and it partitions space into two labyrinthine regions.

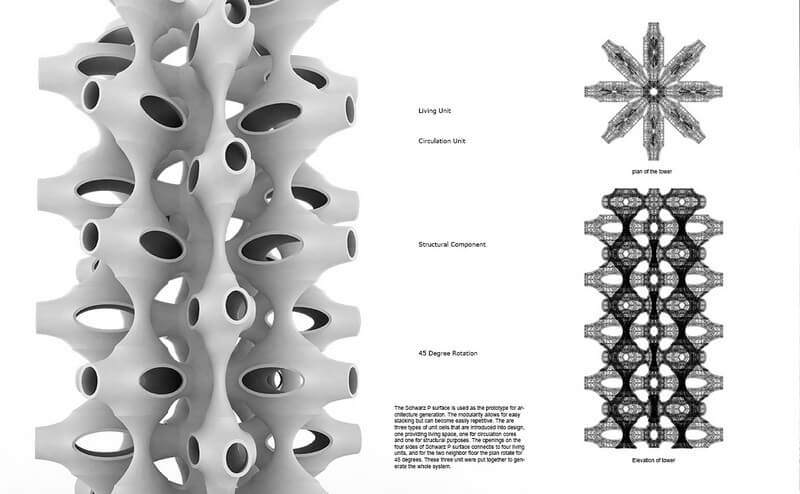
The triply periodic minimal surfaces have a great potential for architecture. How to make architecture to be highly moduliable and replicable is always a main concern for architects. In classical times, when we consider that problem, the five Platonic solids (the cube, octahedron, tetrahedron, icosahedron and dodecahedron), along with the sphere, is the fundamental elements and prototype. However, does high modulization equals stereotype and can innovative design come out of high modulization? Is there a prototype which allows for simple replication yet being innovative in form?

When you consider the answer for this question, then Triply periodic minimal surface certainly comes to your mind. First of all, it has numerous variations to accommodate different architectural functions. Secondly, the space that is formed is constantly continuous, and the splendid horizontal parallel space is available.  It starts from a simple patch which is controlled by the five Platonic solids, by rotating and repeating, it could form an extremely complex shape.

One important character about minimal surface is that it has separable properties, meaning: any sub-patch, no matter how small of area, cut from a minimal surface it still has the least amount of area of all surface sub-patches with the same boundary. Triply periodic minimal surfaces is formed by a fundamental unit copying or mirroring itself three dimensionally.

The fundamental unit always share a face or part of the face with the unit that is immediately surround it. And the fundamental unit can furthermore be subdivided into surface patch, which is also called an “asymmetric unit”. The surface patch is always controlled by a polyhedron. When it is copied by applying the transformations, it produces a tiling of the space and then forms the fundamental unit.

The minimal surface can be specified by the surface patch and the symmetry. Since every minimal surface is unique in surface patch and symmetry, this is what differentiates the types of minimal surfaces.