Voronoi Architecture

Inspiration from nature in the design process is a very widely used method. Architects and designers take advantages of aesthetic features and structural systems of the objects found in the nature. Voronoi diagrams also known as Voronoi tessellations emerge at different scales in nature’s cell structures, honeycomb and animals fur patterns. Architects and designers use this diagram to obtain a more organic looking design, rather than imitate directly from nature.

The Voronoi diagram is a system that divides the space into sub-spaces in an organic way. The diagram uses points to create cells that surround these points. Points can be placed as spontaneously or can be determined in the direction of a certain data and tessellation can be provided accordingly.

Use of Voronoi diagram in fields such as architecture and urban design has increased with the widespread of use of parametric design in architecture. Architects use the Voronoi diagram especially to obtain an organic structure and natural pattern in facade designs. In the academic field, new possibilities that use of the Voronoi diagram can provide for urban design and spatial design are being evaluated.

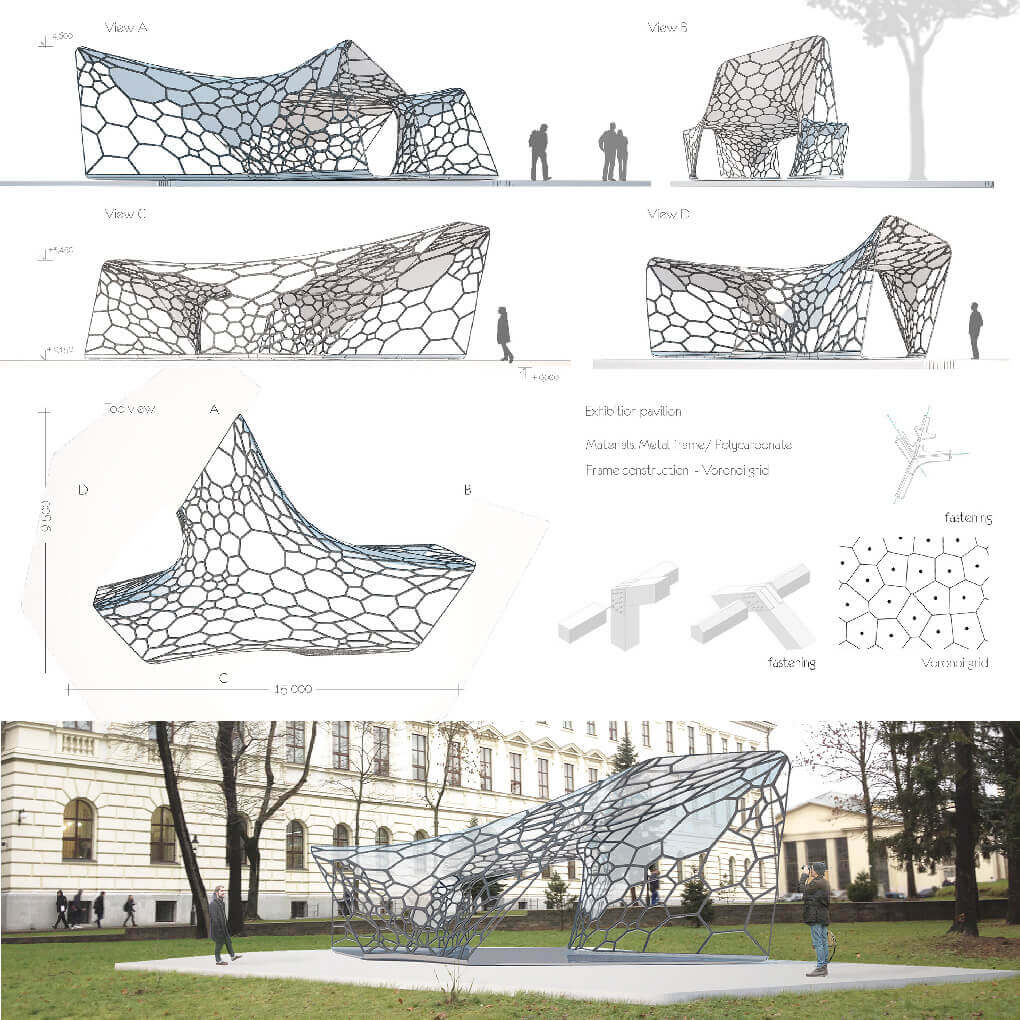
In the context of innovative patterns for tall buildings, Voronoi tessellation is certainly worthy of interest. It is an irregular biomimetic pattern based on the Voronoi diagram, which derives from the direct observation of natural structures.

In mathematics, a Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. In the simplest case, these objects are just finitely many points in the plane (called seeds, sites, or generators). For each seed there is a corresponding region, called a Voronoi cell, consisting of all points of the plane closer to that seed than to any other. The Voronoi diagram of a set of points is dual to its Delaunay triangulation.

The Voronoi diagram is named after Georgy Voronoy, and is also called a Voronoi tessellation, a Voronoi decomposition, a Voronoi partition, or a Dirichlet tessellation (after Peter Gustav Lejeune Dirichlet). Voronoi cells are also known as Thiessen polygons. Voronoi diagrams have practical and theoretical applications in many fields, mainly in science and technology, but also in visual art.

It is used to search the nearest neighborhood, determining position function (nodes), finding largest empty circle (cells) and path planning (edges) and many including architectural design and urban planning.

The task of architecture is to create intelligent spaces. Voronoi patterns can be modelled by the use of parameters to build spatial relationships.

References:

link 1

link 2

link 3
Images:
Google image
Youtube/Luca Massignani
Youtube/ Maker Tales
Pintrest