Adaptive Parameterisation

This thesis by David Stasiuk is concerned with the feature space that defines the inputs and outputs of parametric models for architectural design and project development. As computational design methodologies continue to mature in theoretical and applied terms for both academic and professional practices within the building sciences, the modelling processes, systems and setups they employ become increasingly specialised and powerful.

A proliferation of authoring tools and programming libraries enables the deployment of computational algorithms that support: increasingly sophisticated generative modelling techniques; improved simulation capabilities; models that are informed by material properties, and indeed may program matter themselves; design systems modelled across multiple scales; improved analytical and evaluative techniques; and continuously advancing digital fabrication processes.

Within a given project, a collection of such discrete and variably-purposed systems or representations operates as a network of partial models. As the number and variety of functions for these partial models increase in complexity then, so the information thresholds – or parameter spaces – between them similarly become more numerous, and crucially become increasingly essential to efficient and robust project design, development, and delivery.

This thesis presents Adaptive Parameterisation as a modelling methodology – within both theoretical and applied frameworks – that focuses on the formulation of this feature space for its potential to improve the performance of model networks in the building sciences.

This approach relies on the development and deployment of parameter spaces whose data structures work as mutable substrates for managing and conveying the increased design intelligence created through the dynamic activation of algorithmically-driven, computational modelling systems.

This thesis describes how certain data structures may better support the establishment and implementation of bi- directional constraints between partial models, eliciting increasingly holistic performances from the various, discrete partial models that are necessarily bound together in the realisation of architectural projects.
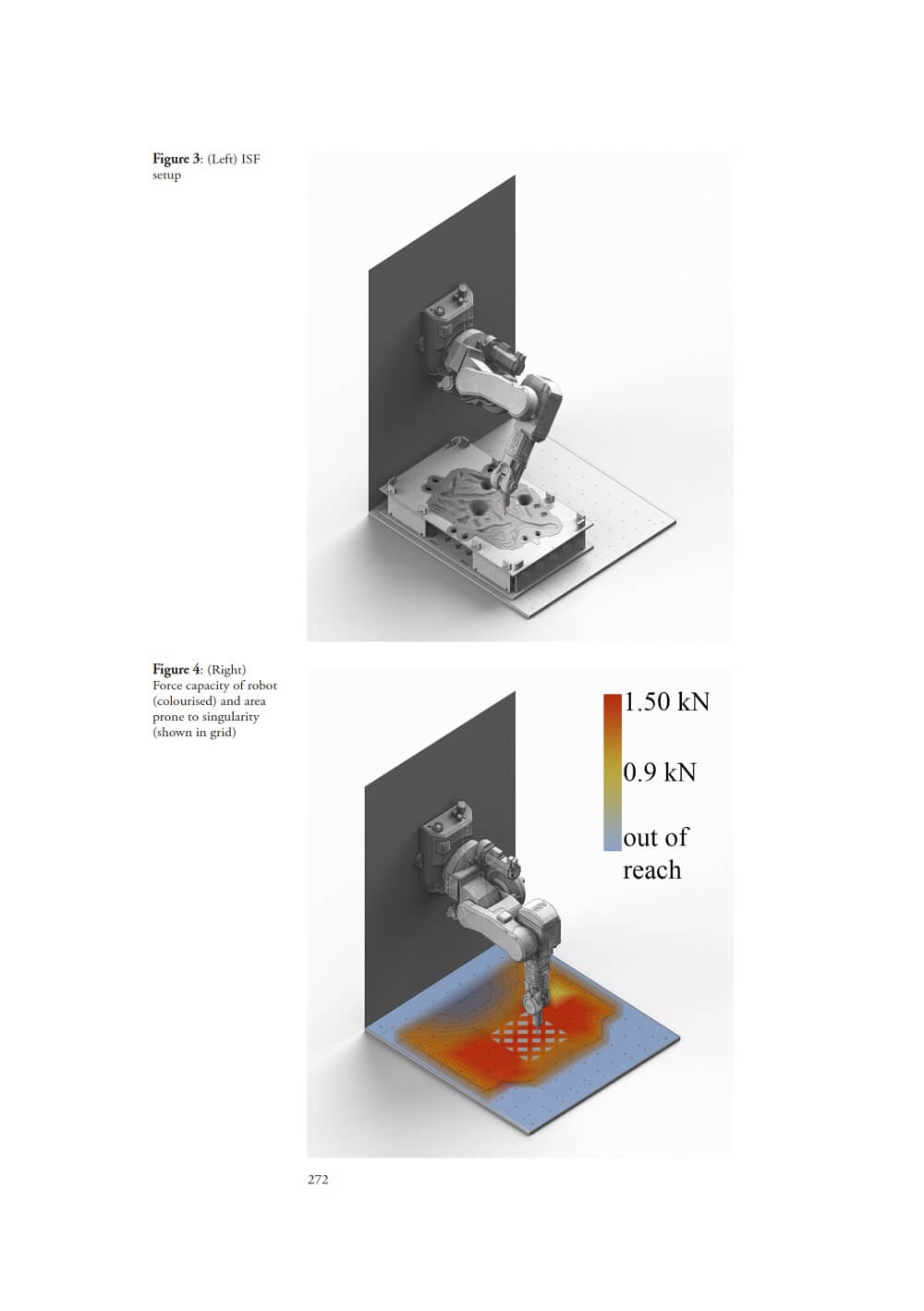
It examines data structures that improve both the descriptive depth and breadth for the parametric models they inform, and which further clarify the purpose of each partial model, while assisting in negotiating the emergent heterogeneity of these purposes across the model network.
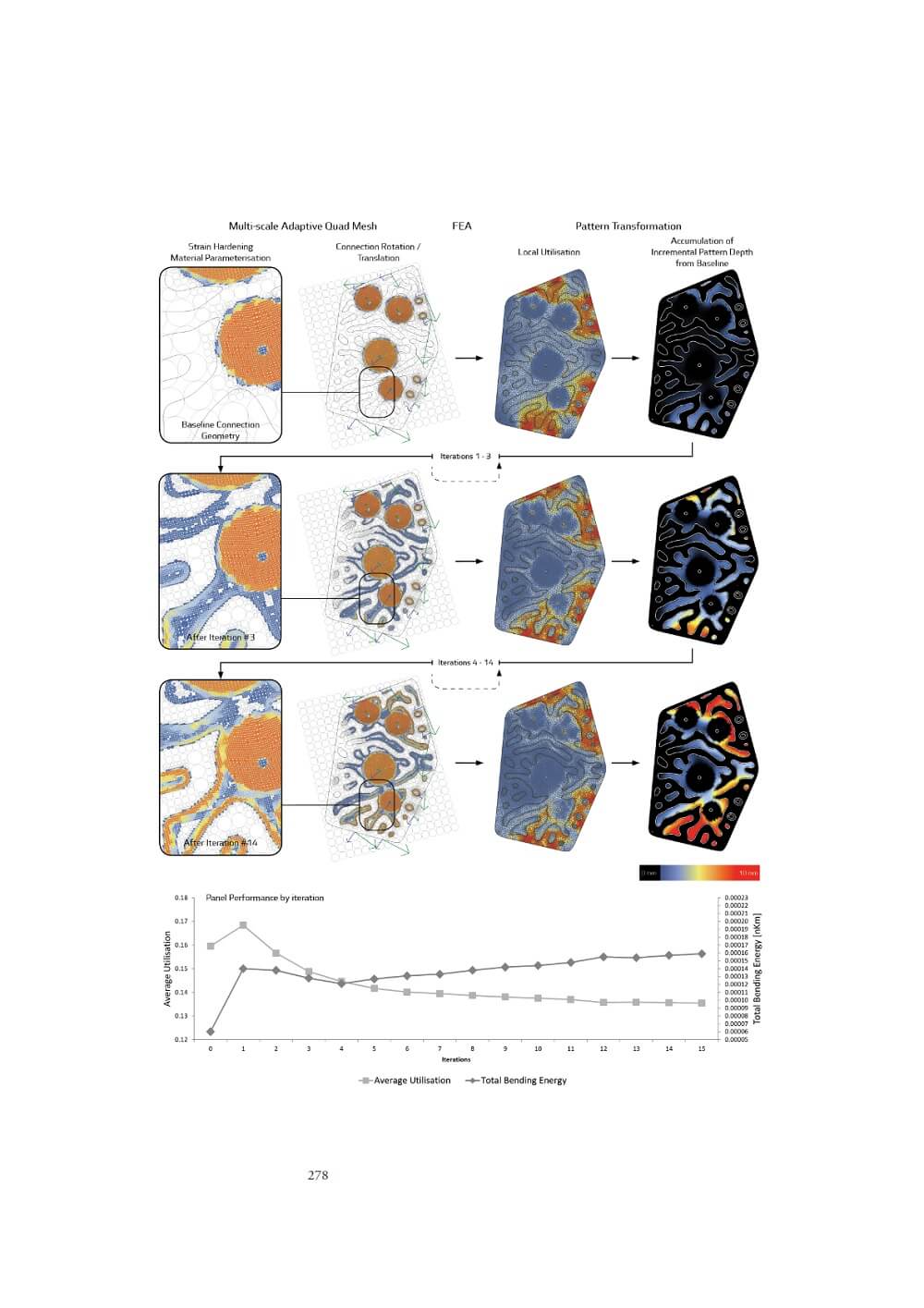




























Comments