Bioinspired mathematical model to establish complex patterns for parametric facades

Natália Queiroz¹ and Fernando Oscar Ruttkay Pereira²

¹Architect, Master in product design at Federal University of Pernambuco.

²Civil engineering. Ph.D. at School of Architectural Studies, University of Sheffield, England.

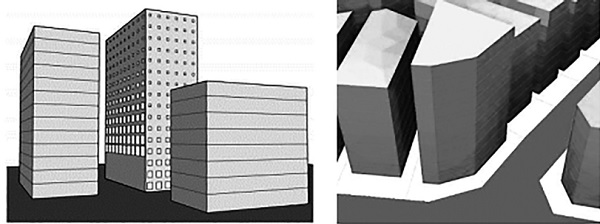
Figure 1. Left: the solution found to establish the minimum of natural lighting in indoor spaces. Right: a radiation analysis and impact variations in different facades.

The facade is the skin that filters and promotes the interaction between the interior and exterior of the building.

During its conception process, one must understand environmental patterns, observe the incident climate, and propose solutions that consider the use of the building and take advantage of the climate´s opportunities, filtering advantages and disadvantages.

Figure 2. Parametric solutions in facades. Fritted glass and shading devices. Often the solutions are just for aesthetic aspects.

Facades are composed of opaque and transparent elements, closed and open, and the openings are the elements that promote the greatest connection between the external and internal environments.

Figure 3. Study of complex facade elements with four levels of patterns.

Recent design explorations consider parametric modeling and digital fabrication as strategies to establish and manufacture complex facade solutions.

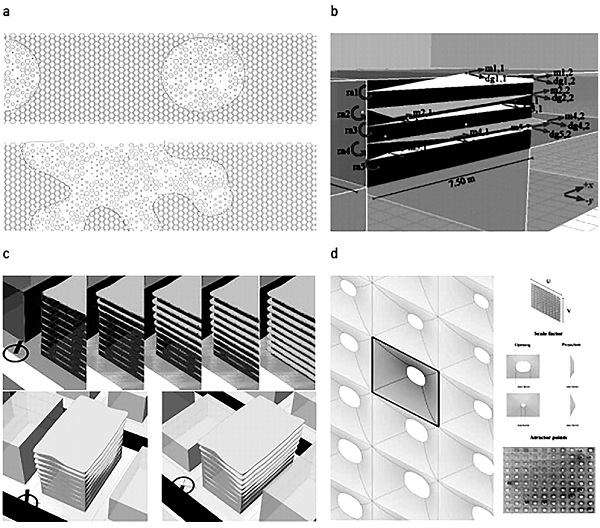
Figure 4. a) shows a fixed pattern solution with high restriction, b) shows a free system solution with patterns to be defined by an optimization process, c) and d) shows mixed pattern solutions that permit a diversity of patterns solutions with limited restriction systems.

Nevertheless, these solutions often disregard their selective filtering function, thus the solutions are established frequently through aesthetic requirements.

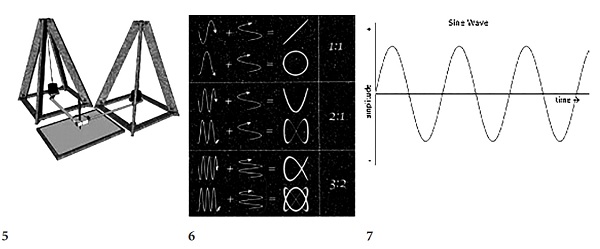
Figure 5. The Harmonograph. Figure 6. Some results in a pendulum Harmonograph. Figure 7. Characteristics and values of a sine wave.

The complexity of modeling the building skin solution associated with performance requirements hinders an approach compatible with bioclimatology, efficiency, and biomimetic requirements, as it increases the mathematical problem complexity for optimization processes associated with environmental characteristics.

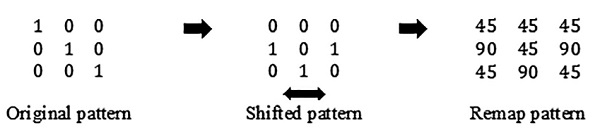
Figure 8. Additional steps included in the Grasshopper component.

This paper presents a mathematical model inspired by nature and its principles to simplify form-finding processes of complex solutions in responsive facades.

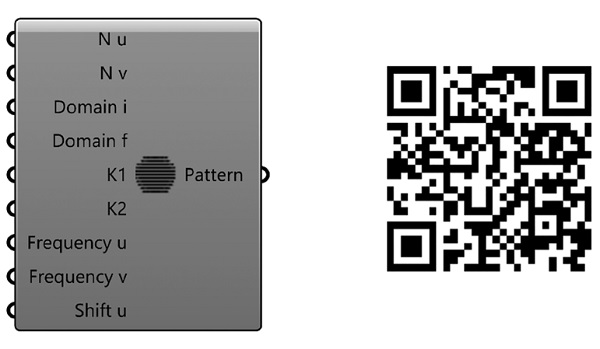
Figure 9. The Grasshopper component and a QR code for download.

The result features a flexible simplified algorithm capable of generating patterns for any kind of shading devices and/or opening solution, in order to facilitate the modeling and optimization processes of facade solutions. The generated algorithm is applied using Python script, Grasshopper and Rhinoceros 3D.

Figure 10. Patterns with the values used.

According to Kolarevic, parametric design designates the use of parameters in the design process. Considering that any design process is based on parameters, the term can be redundant.

The term designates the use of associative digital models consisting of variable parameters and constraints.

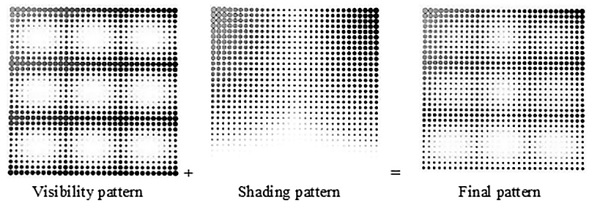
Figure 11. Sum of two patterns, establishing a new solution.

Parameters can be numerical based on geometry, or process automation, and also performance-based, when associated with data analysis and analysis cycles.

The biomimetic design method is related to the performance-based design process since every natural solution is associated with its intrinsic performance, which is related to the formal characteristics of the solution.

Figure 12. Use of the mathematical model to optimize a shading solution.

Although still far from the efficiency of nature, the strategy of integrating the analytical steps with the generation of form through parametric modeling processes is an option to reproduce a principle that resembles the form and pattern definitions present in nature.