Computing Curved-Folded Tessellations
Computing Curved-Folded Tessellations through StraightFolding Approximation
Suryansh Chandra1, Axel Körner2, Antiopi Koronaki3, Rachelle Spiteri3, Radhika Amin3, Samidha Kowli3, and Michael Weinstock3
1Zaha Hadid Architects London, UK
2University of Stuttgart Stuttgart, Germany
3AA School of Architecture London, UK

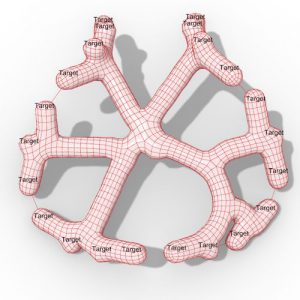
Figure 1: Prototype designed and produced using the method described in this paper.
The research presented in this paper explores curved-crease tessellations to manufacture freeform geometries for architectural and industrial design.
The work draws inspiration from the ease of shaping paper into doublecurved geometries through repeating fold patterns and the observed stiffening of curved surfaces.

Figure 2: Ron Resch’s folding pattern a. flat state; b. folded state.
Since production of large scale curved-folded geometries is challenging due to the lack of generalised methods, we propose an interactive design system for curved crease tessellation of freeform geometries.
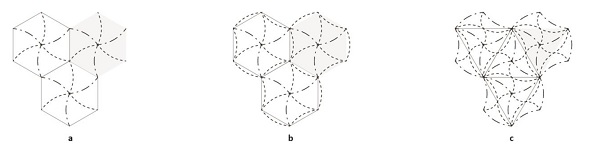
Figure 3: Aggregation of a folded non-inflated degree-3 vertex with hexagonal boundary (a, b) and triangular boundary adaptable to all n-gons (c).
The methods include the development of curved folding patterns on the local scale as well as a novel computational method of applying those patterns to polysurfaces.
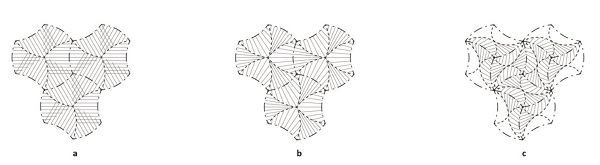
Figure 4: Surface rulings: cylindrical rulings showing conflict (a); conical rulings on hexagonal (b) and n-gon boundary (c).
Using discretized, straightline fold approximations of curved folds in order to simplify computation and maintain interactivity, this approach guarantees developable surfaces on the local scale while keeping the double curved appearance of the global geometry.

Figure 5: Hexagonal Boundary (a); N-gon Boundary (b).
Curved folding offers a very economical method of manufacturing curved surfaces from flat sheet material but a significant obstacle in working with curved-folded geometries is the lack of appropriate computational tools in commercial CAD software for describing such geometries.
As architects and designers, we favour interactive methods that offer direct control over three-dimensional geometry.
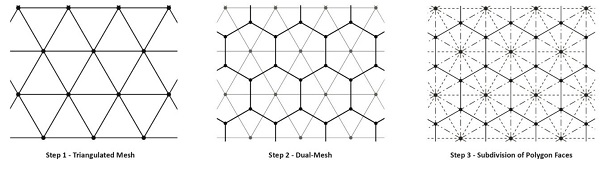
Figure 6: Steps of mesh tessellation: triangulation, dual-mesh and subdivision of polygon faces.
Contrastingly, the methods we have surveyed either require scanning of physical models and planar-quad meshing, or work on smaller scales of bending a singular surface, or require sequentially deriving surfaces through the method of reflection, but do not scale well to geometries with high number of creases.
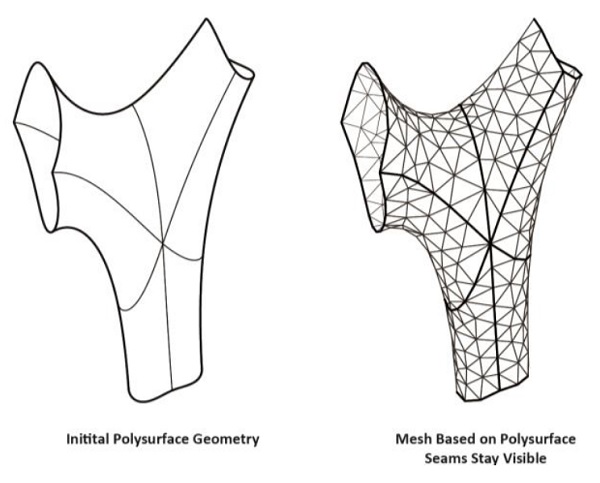
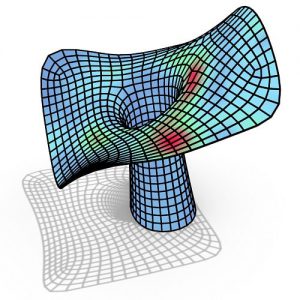
Figure 7: Mesh generated from nurbs patches.
Further, curved-folded surfaces are simple to model physically with a limited number of creases, but substantially increase in complexity with several repeating creases as in a tessellation.
Thus, the primary contribution of this paper is the setting out of a method for designing curved-crease tessellations and describing a simple and intuitive computational framework to simulate these curved-creases on straight-line tessellations.
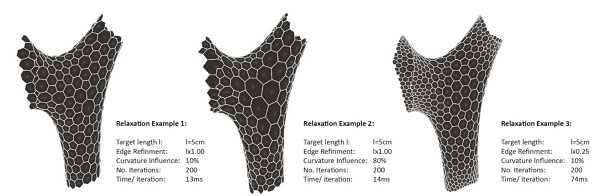
Figure 8: Mesh Relaxation under different influencing parameters.
Critically, it should be pointed out that the geometry simulated by this method is a visual approximation and not precise curved folded geometry.
However it does ensure that the unrolled two-dimensional shapes can be folded and fit together into a predefined form.
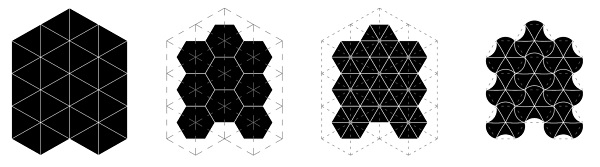
Figure 9: A triangular grid and its derivatives: it’s polygonal dual, a triangular-subdivision mesh, and the curved-fold pattern.
As case studies we investigated Ron Resch’s straight folding patterns, as well as David Huffman’s studies on curved folding.
In Ron Resch’s pattern, polygonal faces (so-called inflated vertices) have straight fold-lines at each vertex, describing triangular faces.

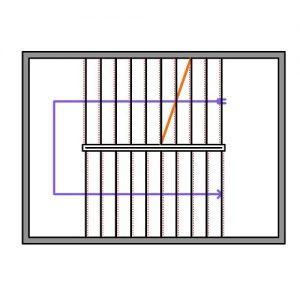
Figure 11: Using a modified Prim’s algorithm to produce developable strips of triangles.
Aggregations of this folded pattern across a grid lead to global curvature. However, when all fold-lines converge into one vertex (so-called non-inflated vertex) instead of a polygonal face, it is not possible to fold the pattern with straight-line creases. David Huffman investigated patterns with even number of curved creases on inflated and noninflated vertices.

Figure 12: Converting strips of unrolled triangles to curved creases.
In this paper, we have demonstrated a method to design curved folded surfaces and a computational framework to apply them to freeform surfaces, producing fabrication data that ensures consistent assembly.
Further, the method presented is applicable to any freeform surfaces that can be tessellated into convex polygons. Figure 14 summarises the method presented including future developments planned.
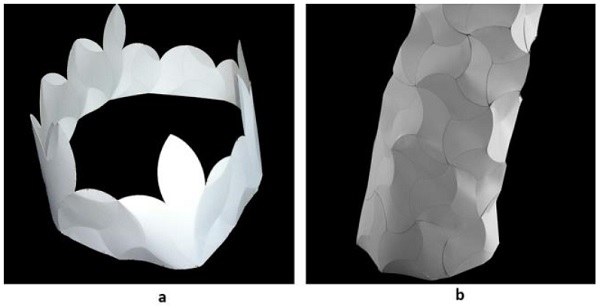
Figure 13: Boundary condition with small tessellation size (a), and the reworked boundary with large tessellations.
The domain of curved folding offers exciting potentials in architecture and manufacturing, but it remains largely unexplored.
With the recent developments in computer hardware and the sophistication of tools available to architects and designers, it is becoming increasingly feasible to work with multi-constraint optimization algorithms such as those required for curved folding.
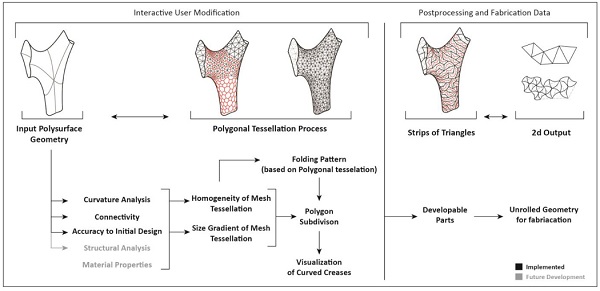
Figure 14. Logic Diagram of the proposed system including future development
The method presented offers numerous opportunities to inform parameters such as folding depth, tessellation size, etc by external criteria such as required structural performance, material specific attributes, etc.
We hope to further this work by enriching it with relevant contemporary research in related fields such as Gattas and You’s recent analysis of structural performance of fold-core panels demonstrated the benefits of panels with curved-folded cores over straight-fold ones highlights the potential of using curved folds to lend stiffness to surfaces.
























Comments