Curved-Crease Origami

This thesis by Ting-Uei Lee systematically explored the design and utilisation of elastically-bent curved-crease origami. This was achieved by developing a set of curved-crease patterns with consideration of the interaction between material elastic bending energy behaviours and origami developability constraints. The thesis makes the following contributions.

First, an exact analytical surface representation of a curved-crease pattern was developed by introducing the 1D elastica solution for large elastic bending deformation into the mirror reflection curved-crease origami generation process. The new geometry, deemed elastica surface origami, is capable of concisely and accurately capturing the principal surface curvature and developability characteristics of elastically-bent curved-crease origami.

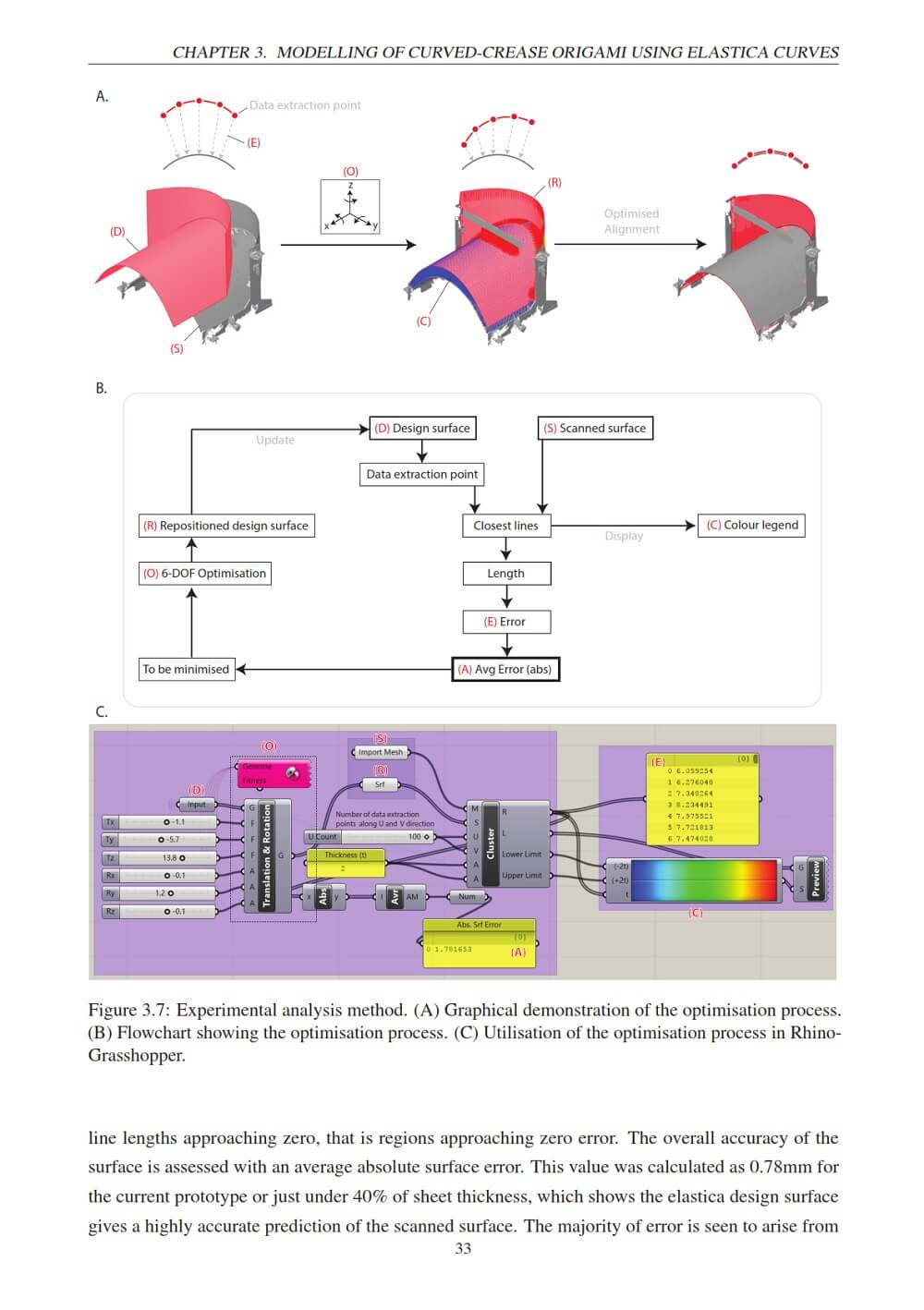
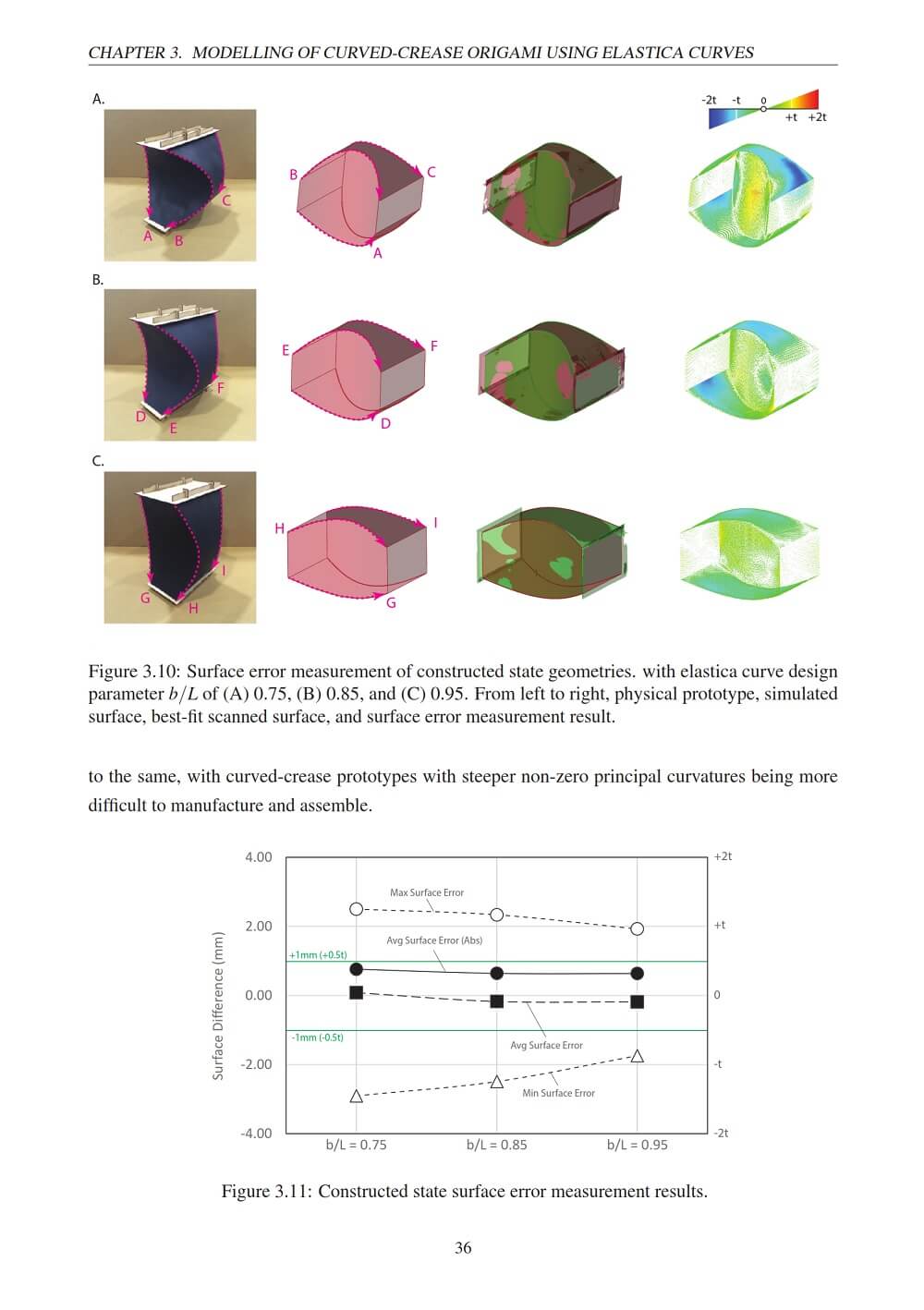
A surface error analysis of 3D scanned physical prototypes was used to validate the analytical geometries, which were shown to be highly accurate to within 50% of the 2mm sheet thickness for a range of elastica surface profiles. Limitations of the curved-crease generation method were also explored including the derivation of a maximum compressibility limit; investigation of accuracy of numerical folding motion simulation; and an investigation of a free edge distortion behaviour which occurred in certain origami forms.
Second, an elastica-derived bending strain energy formulation was used to generate a customizableforce-displacement response in curved-crease compliant mechanisms. This new method was presented by translating the local cross section deployment mechanics to a global frame of reference set according to the design parameters of the curved-crease origami unit geometry.
A valid local-global translation and force-displacement response was found when the cross section deformations with and without developability constraints were suitably close to each other. This key feature enabled a range of predictable non-linear force-displacement responses to be realised through the alternation of pattern edge angle, edge length, and tessellated forms.
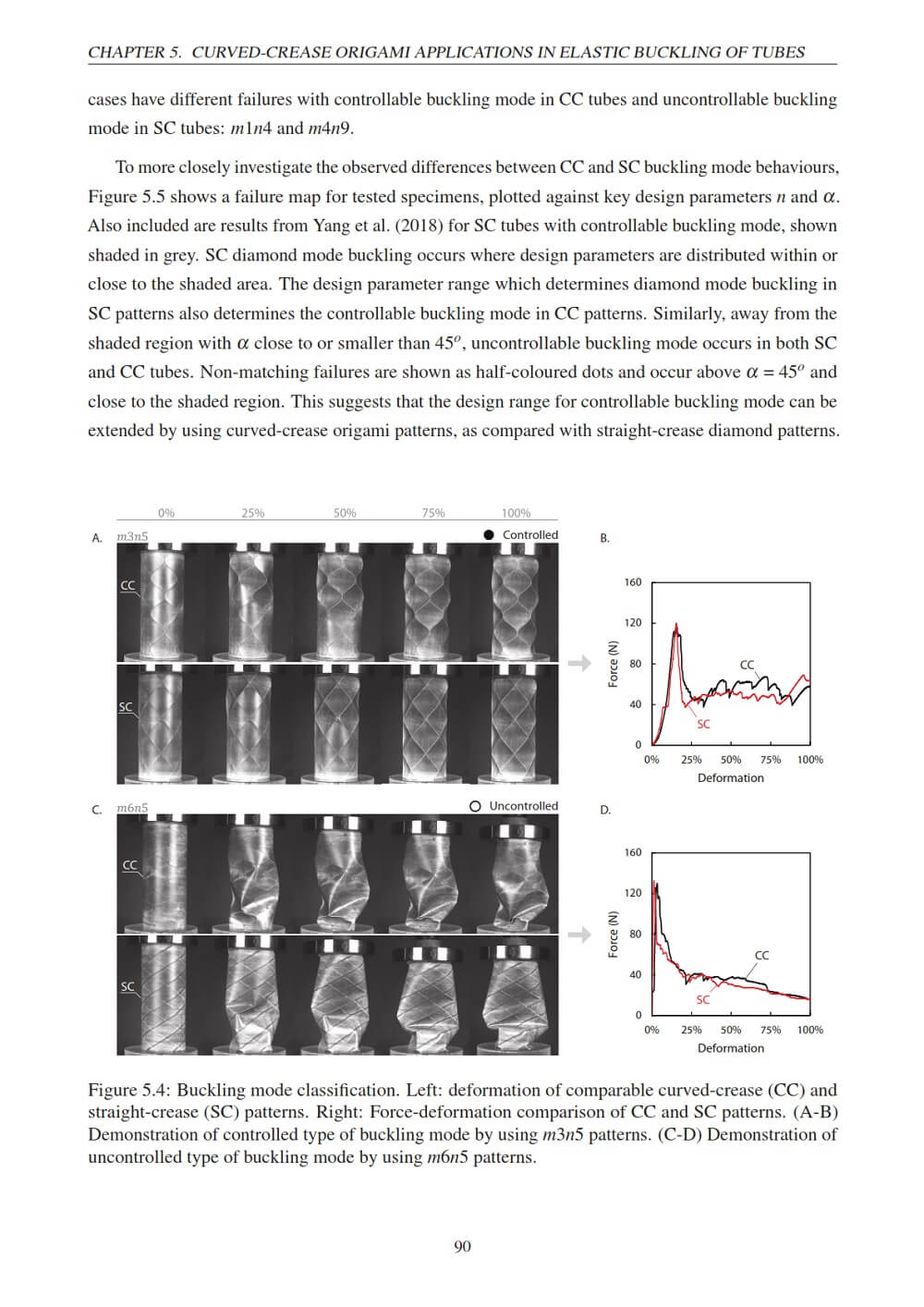
Third, a new application of curved-crease origami was developed for control over the shape of an elastically-buckled thin-walled cylinder, using pre-embedded crease lines. The failure mode was pre-determined as a stabilised high-order elastica surface, which manifests via a diamond buckling mode, similar to imprecise failure modes known to occur in cylinders of this type. A set of prototypes were tested and showed that the buckling process can be guided to a range of designed failure modes.
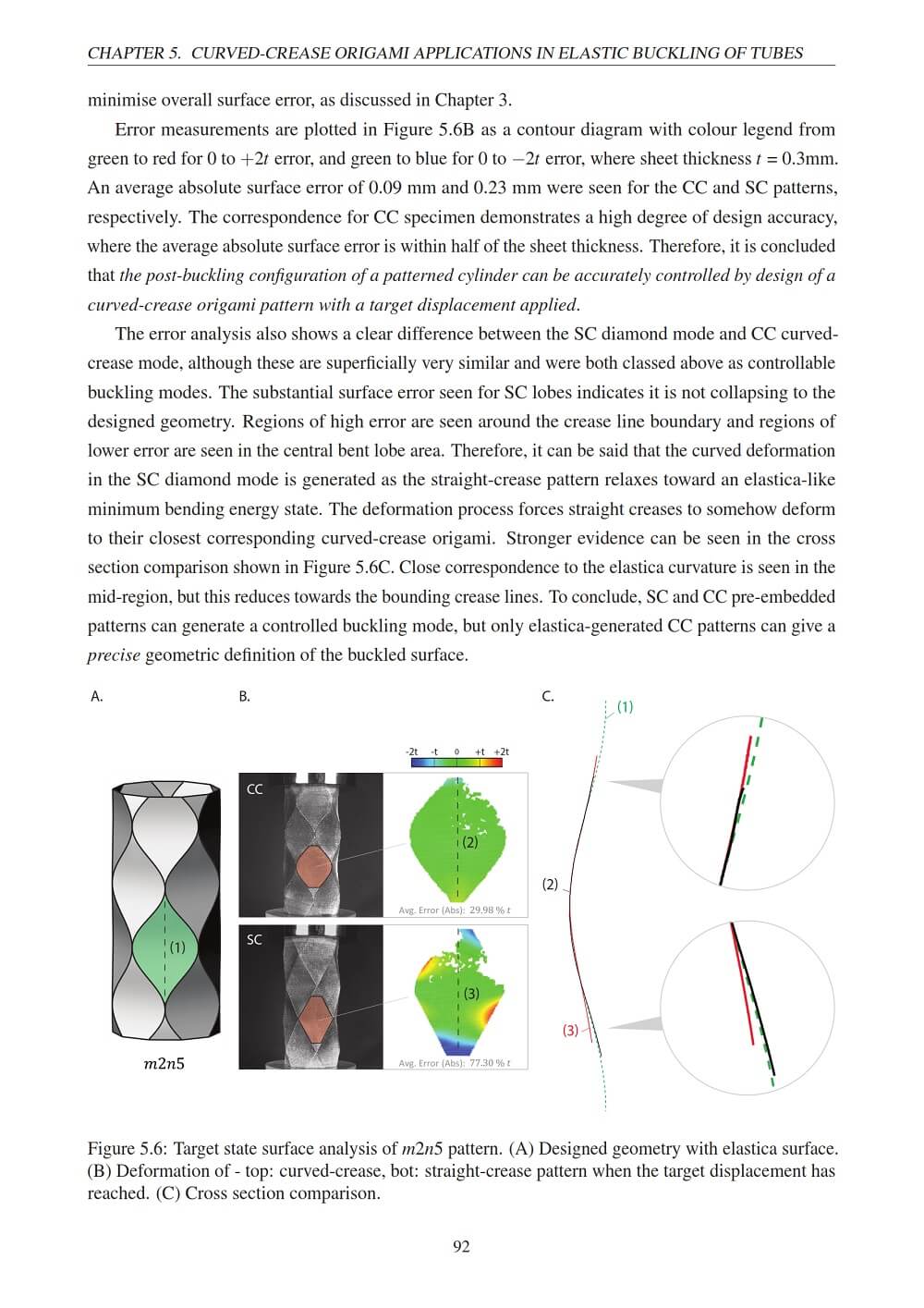
The deformed surface was measured and shown to have a near-exact correspondence to the analytical geometric description. Finally, the investigation into the driving mechanics of the buckling process was closely explored. It was found that the controllable buckling process exhibited a bistable transition from a higher strain energy tubular state to a lower strain energy curved-crease state. Overall, this thesis has made a significant contribution to the research field of origami engineering and large deformation non-linear mechanics. It offers a strong research platform for curved-crease origami ranging from the fundamental geometrical relations to potential engineering applications.




























Comments
jflee1020
Big thanks to Parametric House for sharing my thesis. More information about my work can be found on: http://www.jefflee-digital.com.
Cheers,
Ting-Uei (Jeff) Lee
parametric
Good job 🙂