Digital Design Process

CURVED.IT: A design tool to integrate making with curved folding into digital design process

Saadet Zeynep Bacinoğlu¹, Luka Piskorec², Toni Kotnik³

¹Graduate Program of Architectural Design Computing, Institute of Science, Engineering, and Technology, Istanbul Technical University, Istanbul, Turkey

²Department of Architecture, School of Arts, Design, and Architecture, Aalto University, Espoo, Finland

³Department of Architecture, School of Arts, Design, and Architecture, Aalto University, Espoo, Finland

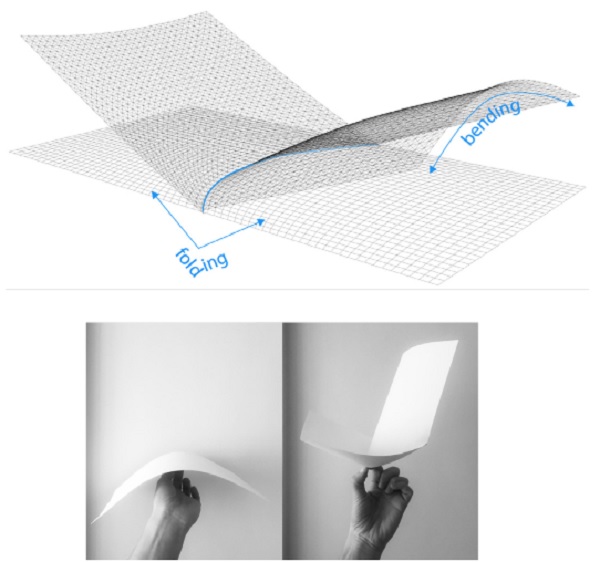
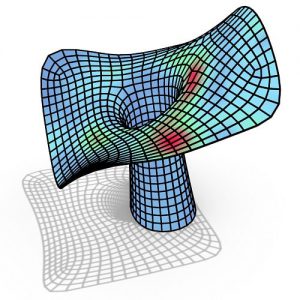
Figure 1. Curved folded geometry.

The act of changing the direction of a sheet surface along a non-straight curve is a specific case of curved folding. From an architectural point of view, curved folding is an exciting operation. One or a couple of operation can generate highly complex shell-like spatial enclosure.

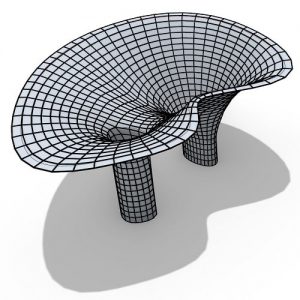
Figure 2. Free-standing units of One Fold by Patkau Architects (2017).

From a digital design perspective, the implementation of curved folding with the built-in toolsets of available computer-aided design softwares is a challenging problem. The equilibrium state of curved folded geometry is needed to be found with a computational form-finding strategy.

Figure 3. Applications of curved folding in architecture.

To use curved folding as a digital design operation, we introduce a new tool through developing a digital procedure for form-finding. The tool we develop can enable the experimentation with curved folding in the early stage of design process and facilitate the subsequent design development.

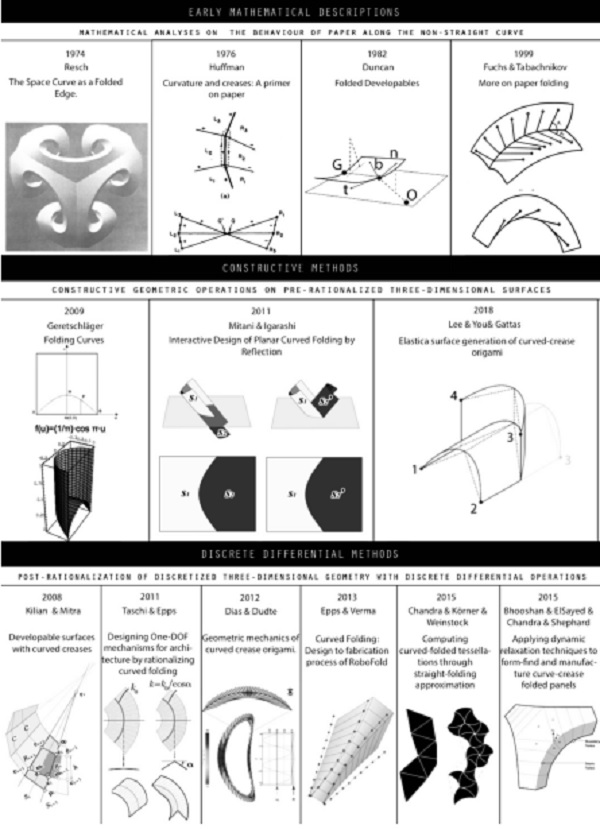
Figure 4. Geometric approaches to represent curved folding with a computer.

In this article, we briefly present the literature focusing on curved folding in computational geometry, as well as the scope and description of a subclass of curved folding operation. Then, we introduce a digital tool, CURVED.IT through a design manual for its implementation and an algorithmic framework for its extension. Lastly, we discuss the design examples generated by CURVED.IT, and the potentials of the tool.

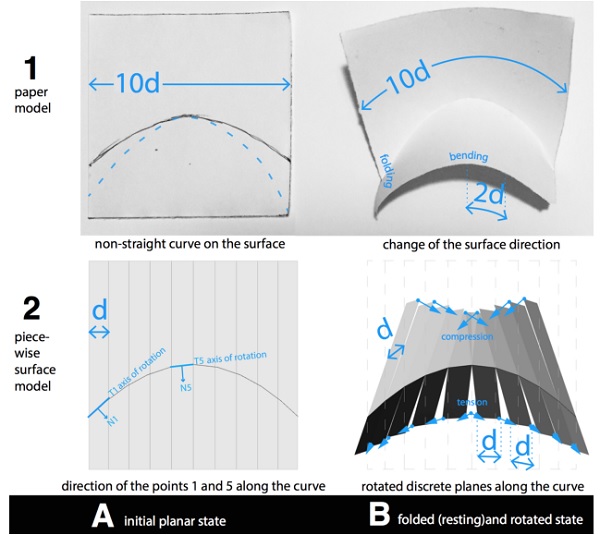
Figure 5. Curved folding of single sheet surface and pieces of the surface.

This research is derived from the exciting potential of a particular technique, curved folding, for architecture and structures. A specific case of curved folding technique is the action of changing the direction of a surface along a non-straight curve on the sheet surface.

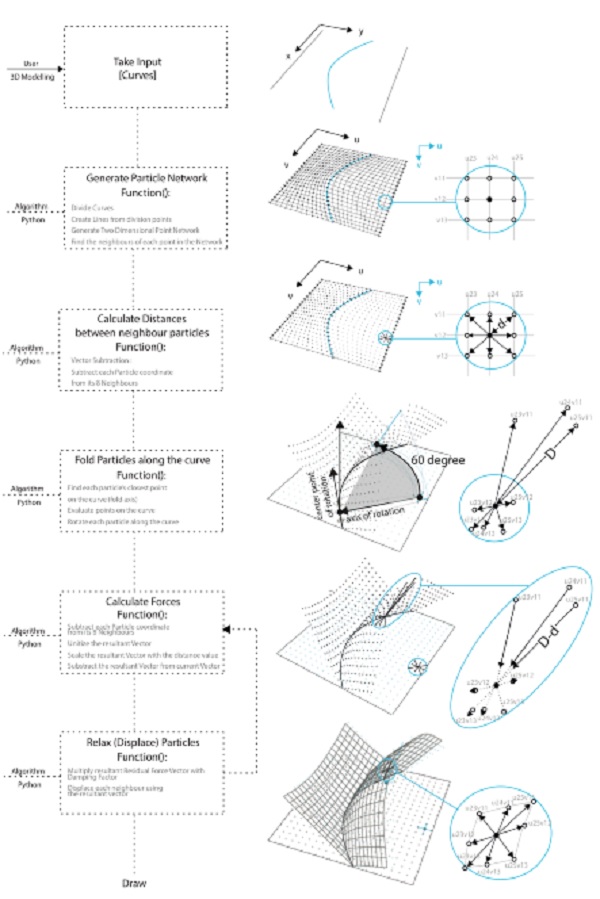
Figure 7. Steps of the dynamic relaxation (DR) algorithm.

When the sheet is folded along a non-straight curve, the three-dimensional configuration of the sheet comes to a resting state through a combination of folding and bending. While the pure folding transfigures the sheet to a polyhedral surface with an abrupt change in the surface direction, the act of bending forms the sheet to a smoothly curved surface with a gradual slight change in the surface direction.

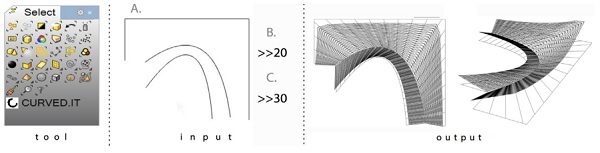
Figure 8. The access to CURVE.IT in Rhinoceros environment.

The interesting point of curved folding is the complex three-dimensional form that is generated by this hybrid surface deformation. In this form, the slender sheet gains strength and become more resistant to buckling.

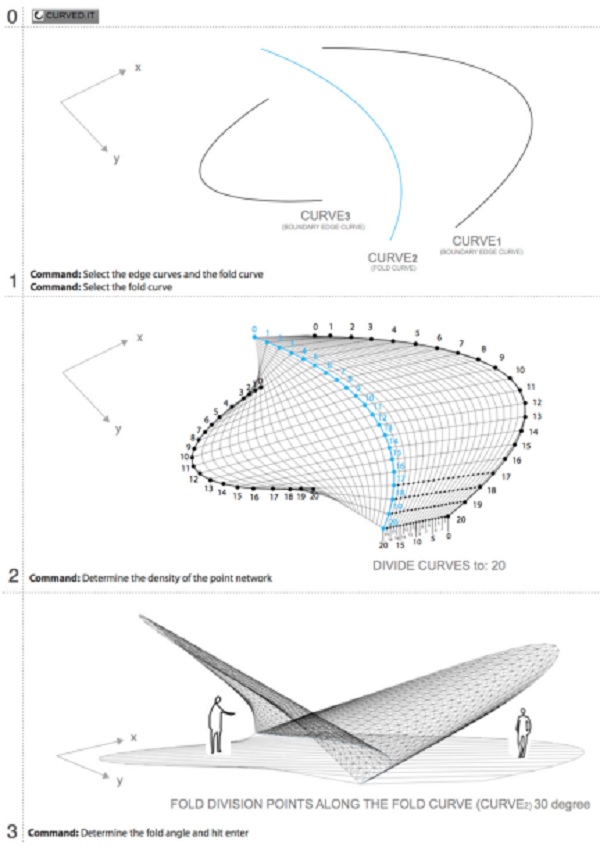
Figure 9. Generation of a curved folded space with three instructions of CURVED.IT.

In an architectural context, curved folding technique can be used as a design operation. The smooth and abrupt surface deformations that are generated with curved folding can provide architects with the generation of complex geometries that host different spatial situations and performative capacities.

Figure 10. A simple demonstration of variations by changing the combination of three simple curves.

A simple example by Patkau Architects demonstrates the spatial and structural potential of the 304×731 cm folded sheet with one single fold. The folded surface is self-standing by solely touching the ground from two points.

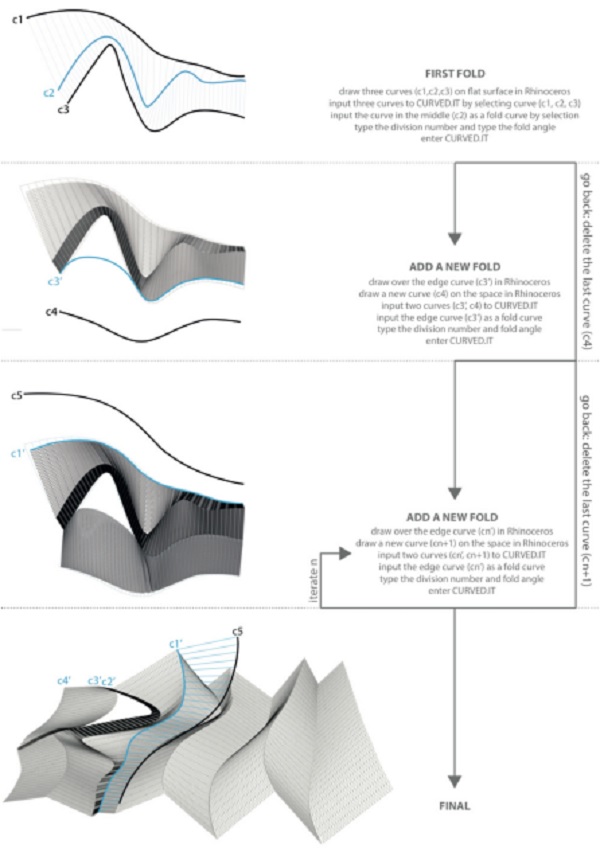
Figure 11. Demonstration of the addition of new folds step by step.

In the problem of curved folding, the challenge is to understand and measure the resultant three-dimensional configuration of the curved folded sheet when it is manually modeled. The resultant three-dimensional form is “a resting state of the deformed two-dimensional sheet which goes beyond the mathematics of developable surfaces to a question of physics: equilibria of an unstrechable surface with uncreased and creased portions folding elastically toward desired angles”.

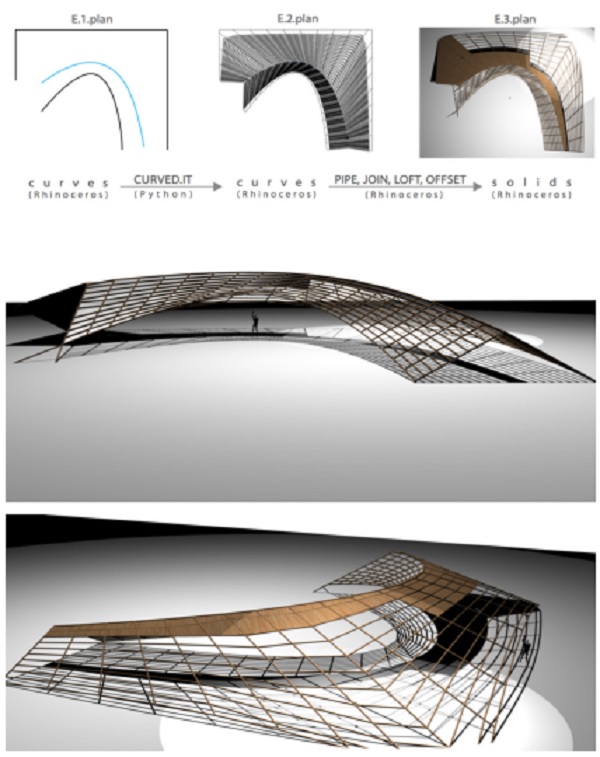
Figure 12. The applied pipe and surface functions in Rhinoceros to CURVED.IT form.

Therefore, the computational form-finding strategies provide an appropriate method to find the equilibrium state of the curved folded geometry in the digital environment.

Figure 13. The process of transforming the resultant set of lines to the solid geometries.to CURVED.IT form.

In this study, we transferred curved folding to the computer environment through developing a computational form-finding strategy in Python language within Rhinoceros environment. The main goal of this study is to introduce a design tool that allows a specific technique, curved folding, as a design operation in the computational process to explore spatial forms.

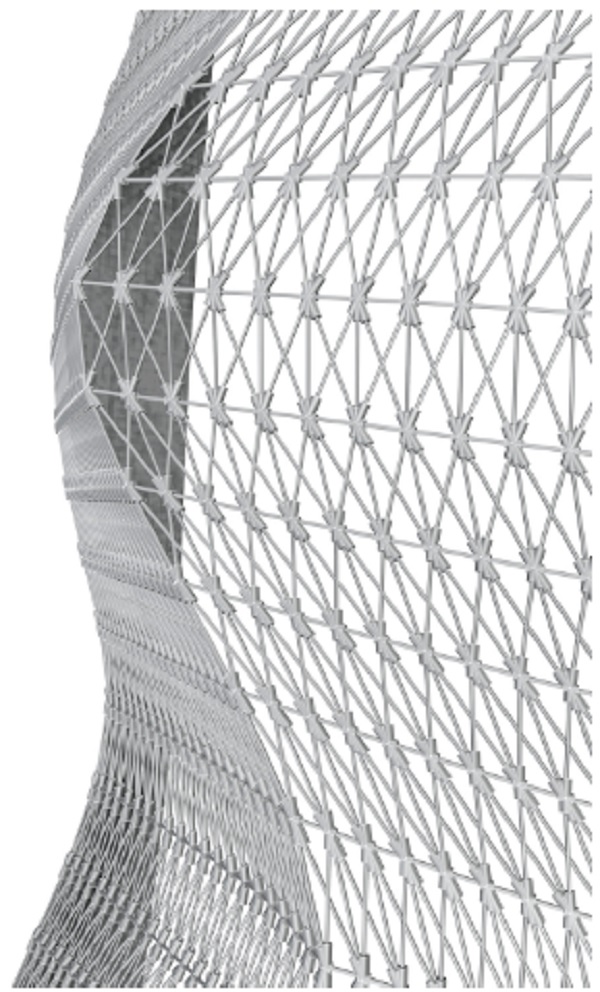
Figure 14. The generation of a joint detail by applying the in-built Rhinoceros pipe function to the one-tenth of each line segment.

The essential contribution of this study is a proposed digital form-finding tool for the architects and the designers. The proposed tool can be easily used in the early stage of the computational design process to generate curved folded geometries.

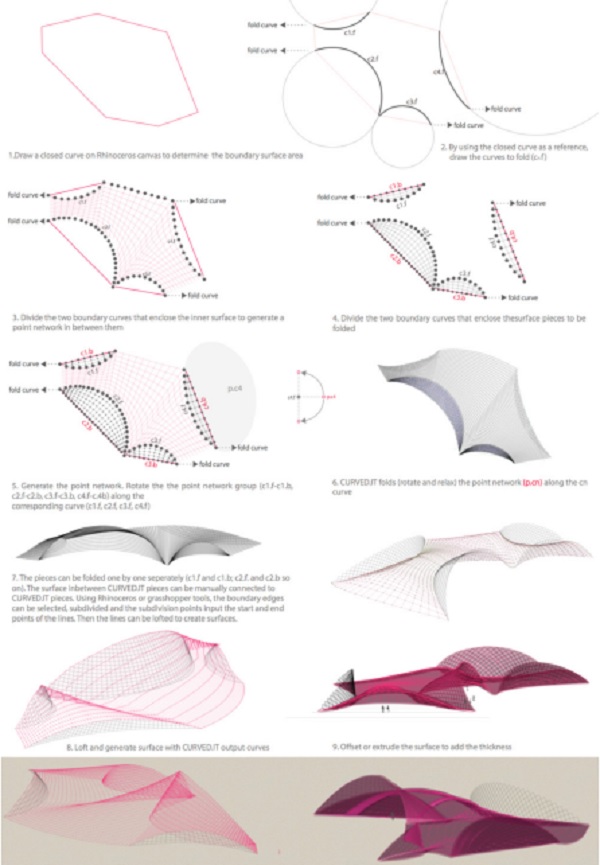
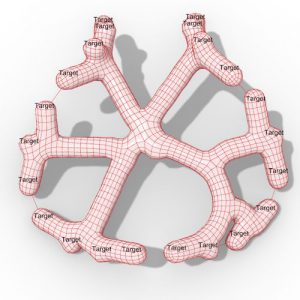
Figure 15. The experiment with multiple non-parallel curved folds.

This article presents the literature focusing on curved folding in architecture and computational geometry, as well as the scope and the description of the curved folding technique. Then, the article introduces a design tool, CURVED.IT, by explaining how the proposed algorithmic framework integrates curved folding into the early stage of the computational design process. Moreover, it presents the design manual for the architects by explaining the steps to be taken for the form generation. Lastly, it discusses the shortcomings and the potentials of the tool.