Funicular Gridshells

On funicular gridshells and Airy stress functions

Cameron MILLAR^a, Toby MITCHELL^b, Arek MAZUREK^c, Ashpica CHHABRA^b, Alessandro BEGHINI^b, Allan McROBIE^d, William F. BAKER^b

^aMillar Consulting

^bSkidmore Owings & Merrill

^cMazurek Consulting

^dDepartment of Engineering, University of Cambridge, UK

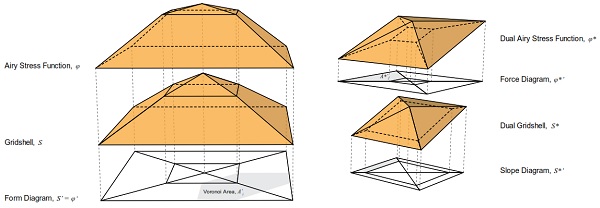
Figure 2: Plane faced gridshells and Airy stress functions are defined using these terms. and ∗ , and ∗ , ′ and ∗ ′, ′ and ∗ ′ are reciprocal pairs.

2D graphic statics is a method originating in the 19 th century to analyse and design pin-jointed trusses using two reciprocal diagrams; the form diagram, which describes the structural geometry, and the force diagram, which describes the forces within the truss.

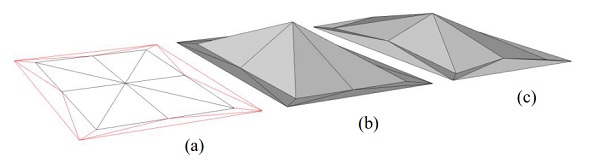
Figure 3: (a) A red restraining frame is added to the form diagram to take the horizontal forces (if any), from the roof structure members which are drawn in black. (b) The roof with the restraining frame in the horizontal plane. (c) The Airy stress function for roof (b) with equal vertical reactions at each perimeter support. Note that the restraining frame in (c) is not confined to the horizontal plane, indicating that it is stressed in the roof (b). Note that (b) and (c) are interchangeable; either one could be the structure and the other the Airy stress function for the same vertical loading. If (b) is the structure, it develops horizontal reactions against the restraining frame whereas (c) does not.

This paper investigates ‘2.5D’ graphic statics for gridshell design. This relies upon the form, force and slope diagrams. The force and slope diagrams combine, via a mixed area calculation, to give the funicular vertical load on a given node.

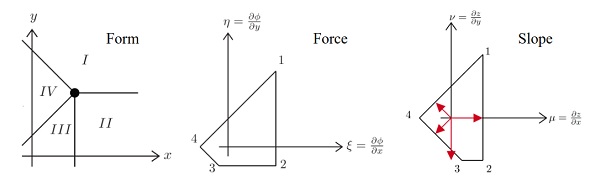
Figure 4: Simple example of the form, force and slope diagrams. The length of the line in the force diagram gives the horizontal force in the corresponding bar. The perpendicular distance of the line from the origin in the slope diagram gives the slope of the corresponding bar in the gridshell (length of red arrows).

In the same way that the force diagram can be constructed from a discrete Airy stress function, so can the slope diagram be constructed from a plane-faced gridshell.

Both the plane-faced gridshell and Airy stress function are planar liftings of the form diagram. This new methodology allows the engineer to visually design the Airy stress function and gridshell simultaneously with the aim of producing gridshells which are both plane-faced and funicular with a given design load, such as a uniform projected loading.

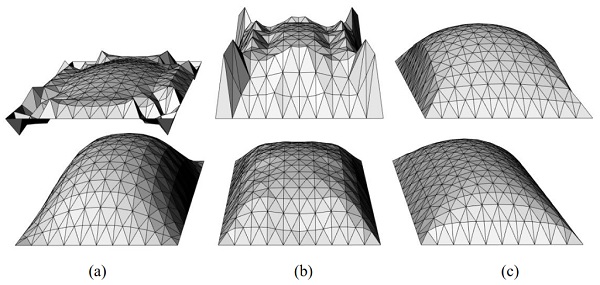
Figure 7: Gridshells (bottom) and their Airy stress functions (top) for uniform projected loading. Note that because of the duality between the gridshell and its Airy stress function, the top row could be the gridshell and the bottom row would be the corresponding Airy stress functions. (a) Negative Gaussian curvature at the corners induces tension into the corners. (b) Teeth-like Airy-stress function along the perimeter indicates some truss action. (c) A pillow shaped gridshell which contains a limited number of tension bars.

Whereas in 2D graphic statics one can control the form and force diagram, here one can control the Airy stress function and gridshell geometry.

This paper also introduces the concept of mixed-Airy gridshells in which the Airy stress function and plane-faced gridshell are interchangeable for the same applied vertical load.

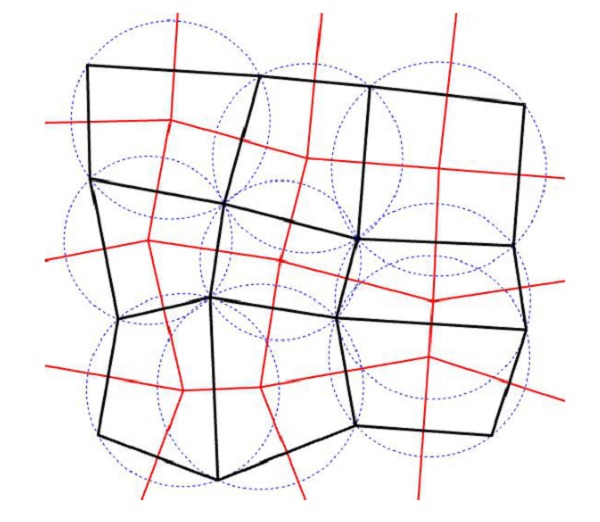
Figure 8: An i-circular mesh is a circular mesh in the form diagram. The mesh is shown in black with the dual/Voronoi diagram in red. The blue circles are the circumscribed circles of the form diagram.

Self-Airy gridshells, where the Airy stress function and gridshell are scaled versions of each other, are also introduced. Focus is given to designing plane-faced self-tied gridshells which do not thrust horizontally against the ground or surrounding structures.

Figure 9: Michell Dome. This is a plane-faced quad-dominant gridshell which is funicular under uniform projected loading – it is a UPL self-Airy gridshell.

2D graphic statics was pioneered in the 19th century by Maxwell, Rankine and Cremona. It relies upon the reciprocal relationship between the form and force diagrams.

Figure 10: Schwarz-Christoffel Gridshell

The form diagram describes the geometry of the pin-jointed truss. The force diagram describes the forces within the truss. It is possible to construct the force diagram from the form diagram through a discrete Airy stress function.

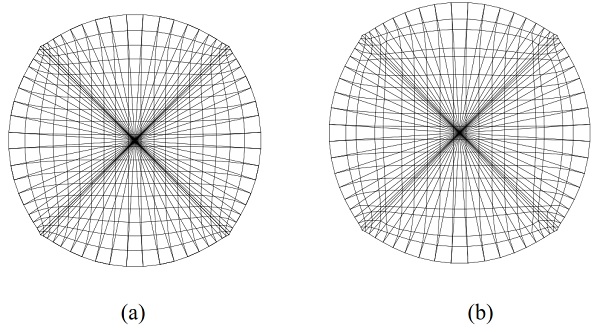
Figure 11: The force diagrams of the Schwarz-Christoffel gridshell. (a) UPL self-Airy. (b) Single lift. Note that near the perimeter of (b), the quads are not uniform in size and are not proportional to the Voronoi.

This is a complete 3D plane-faced polyhedron which projects down onto the form diagram. This polyhedron, , has a dual polyhedron, , defined by a node in one mapping to a plane in the other and a plane in one mapping to a node in the other.

The duality maps a point (, , ) to the dual plane = α + β − . This is called the pole and polar plane and is a part of projective geometry which was well understood in the 19th century.

Figure 12: Strubecker gridshell

The projection of the dual polyhedron, , onto the horizontal plane is the force diagram. This is known as the Maxwell reciprocal diagram and a line in the form diagram has a corresponding perpendicular line in the force diagram whose length is the force in the bar. The concepts of 2D reciprocal diagrams can be taken to 3D with 4D Rankine stress functions and beyond into ndimensions.

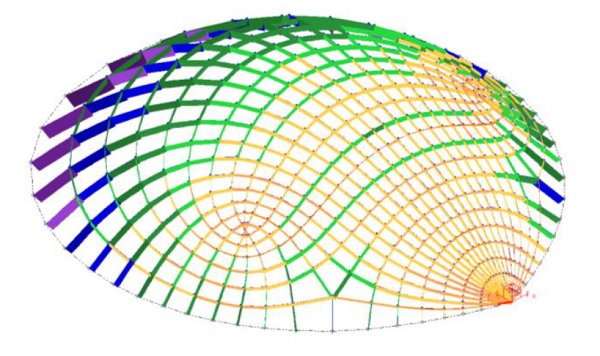
Figure 13: Axial force distribution in the Strubecker gridshell

Plane-faced gridshells can also be described as polyhedrons. Taking the established 2D graphic statics methodology, it is possible to consider 2.5D shells and gridshells with the introduction of the slope diagram.

Gridshells have already been studied using graphic statics; thrust network analysis uses 2D graphic statics in the design of masonry shells and 3D Rankine reciprocals have been used to consider 3D space structures, including gridshells, but have struggled to find common usage due to the Rankine incompleteness problem.