Computational analysis of hygromorphic self-shaping wood gridshell structures

Philippe Grönquist^1,2,3, Prijanthy Panchadcharam², Dylan Wood, Achim Menges⁴, Markus Rüggeberg^1,2 and Falk K. Wittel²

¹Laboratory for Cellulose & Wood Materials, Empa, 8600 Dübendorf, Switzerland

²lnstitute for Building Materials, ETH Zurich, 8093 Zürich, Switzerland

³Institute of Structural Engineering, ETH Zurich, 8093 Zürich, Switzerland

⁴Institute for Computational Design and Construction, University of Stuttgart, 70174 Stuttgart, Germany

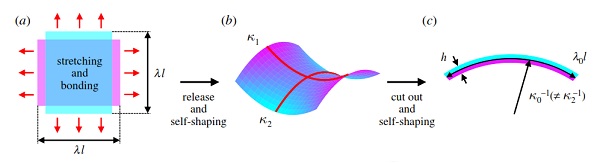
Figure 1. Curvatures of a bilayer-composite. (a) Two elastic sheets of thickness h/2 are stretched by a factor of λ and then bonded together. The same configuration is achievable by first bonding two stimuli-responsive layers together and inducing λ with the stimuli, e.g. a moisture-content change in wood will result in anisotropic swelling- or shrinkage-induced stretches in the single layers. (b) Upon release, the bilayer-composite plate-like sheet self-shapes into an exemplary saddle configuration with principal curvatures κ1 and κ2. (c) A narrow quasi-two-dimensional strip cut out from the sheet displays natural curvature κ0 and stretch λ0 (on the basis of [20,21]).

Bi-layered composites capable of self-shaping are of increasing relevance to science and engineering. They can be made out of anisotropic materials that are responsive to changes in a state variable, e.g. wood, which swells and shrinks by changes in moisture. When extensive bending is desired, such bilayers are usually designed as cross-ply structures.

However, the nature of cross-ply laminates tends to prevent changes of the Gaussian curvature so that a plate-like geometry of the composite will be partly restricted from shaping. Therefore, an effective approach for maximizing bending is to keep the composite in a narrow strip configuration so that Gaussian curvature can remain constant during shaping.

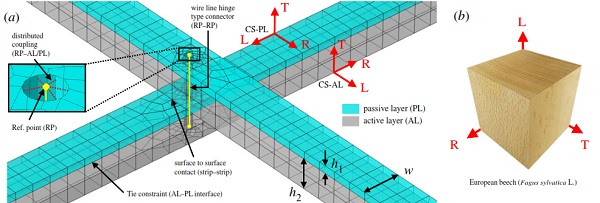
Figure 2. Gridshell FE model set-up. (a) Detail of FE model at strip intersection with parameters h1, h2 and w. Local orthotropic coordinate systems (CS) R, T and L assigned to passive and active layers (PL and AL) of strips. (b) Local anatomical directions R, T and L visualized on a macroscopic cube of European beech wood.

This represents a fundamental limitation for many applications where self-shaped doublecurved structures could be beneficial, e.g. in timber architecture. In this study, we propose to achieve double-curvature by gridshell configurations of narrow self-shaping wood bilayer strips.

Using numerical mechanical simulations, we investigate a parametric phase-space of shaping. Our results show that double curvature can be achieved and that the change in Gaussian curvature is dependent on the system’s geometry. Furthermore, we discuss a novel architectural application potential in the form of self-erecting timber gridshells.

In this study, we show a way to overcome the mentioned limitations by self-shaping gridshell systems (see electronic supplementary material, movie S1), focusing on orthogonal and interconnected narrow wood bilayer strips. Each wood bilayer strip will strive towards shaping to its natural curvature when the humidity is changed, and ideally, the gridshell system will realize a shape where ΔK > 0.

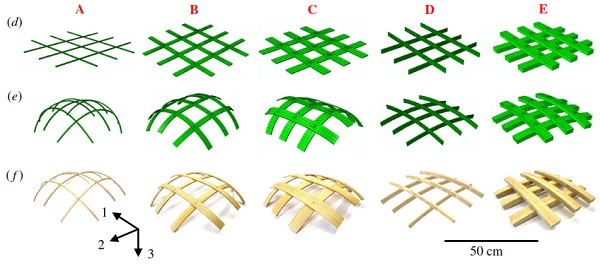
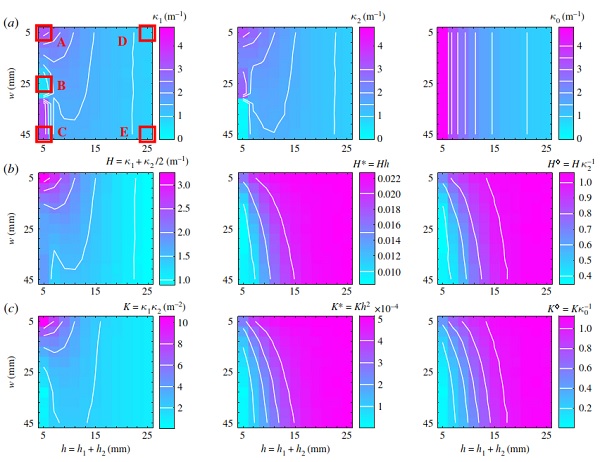
Figure 3. Phase space of gridshell curvatures after self-shaping in dependence of width w and thickness h for 121 (11×11) finiteelement model solutions. (a) Curvatures along middle strips in directions 1 and 2 (κ1 and κ2) and natural curvatures κ0. A, B, C, D, E denote configurations at extremities of analysed phase space. (b) Mean curvatures H, and mean dimensionless curvatures H and HS. (c) Gaussian curvatures K, and dimensionless Gaussian curvatures K and KS. (d) Configurations A, B, C, D, E in initial state (wet). (e) Configurations after self-shaping (dry). (f) Experimental configurations, 1 : 1 physical model rebuilds of the FE models using beech wood.

However, the system’s behaviour, especially the exerted effect of rigid interconnections on the shaping, is yet unknown. In this context, we analyse the self-shaping behaviour of wood gridshell structures at medium scale by parametric numerical studies using the finite-element (FE) method.

By investigating principal curvatures, natural curvatures, mean and Gaussian curvatures, we quantify and discuss the phase-space-dependent shaping behaviour and draw relevant conclusions for application to selfassembly architecture and construction processes. For such applications, gridshell systems offer a lightweight and material efficient method of covering large spaces with structurally performative curved forms.

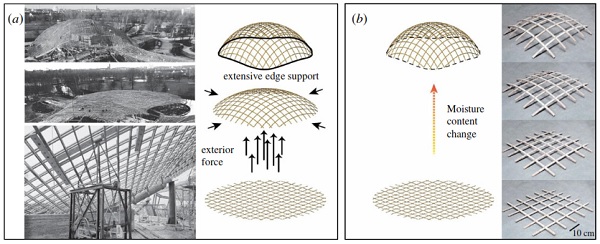
Figure 4. Gridshell shaping procedures. (a) Conventional procedure by shaping the gridshell via exterior forces for active elastic bending; Extensive edge support is needed in the assembled configuration (Photo credit: Institute for lightweight structures and conceptual design, University of Stuttgart). (b) Novel proposed procedure by hygromorphic self-shaping of the single strips (right side: Built 5×5 grid physical demonstrator); no exterior forces and lighter edge support.

Our results show that self-shaping wood gridshells enable positive changes in Gaussian curvature (K), which is impossible for solid plate geometries of single bilayer-composites of anisotropic materials.

The shaping behaviour appears to be dictated by complex interactions between the strip’s thickness and width. On the one hand, for thin and narrow strips, the large change in K is enabled by the inplane bending deformations of the strips of the rigid-jointed grid. On the other hand, for thicker and wider strips with lower changes in K, in-plane bending moments enforce the system’s shaping towards values close to or slightly surpassing the natural curvature of single strips.

The presented self-shaping would overcome many of the constraints of post-formed timber gridshells in the sense that complex lifting and forming is replaced with distributed autonomous actuation. Less structure is needed to constrain the shell after forming, tighter radii of curvature, and more complex lamella interactions would be made possible.