Modeling Developable Surfaces with Discrete Orthogonal Geodesic Nets
Modeling Developable Surfaces with Discrete Orthogonal Geodesic Nets
Michael Rabinowitz
MSc in Computer Science, ETH Zurich
A thesis submitted to attain the degree of Doctor of Sciences of ETH Zurich
 DOGs are discrete analogues of developable surfaces, parameterized through orthogonal geodesics. In the rest of the thesis lies the author’s attempt to persuade readers that DOGs are both useful and interesting, while developing relevant mathematical theory and a set of computational tools for modeling DOGs.
DOGs are discrete analogues of developable surfaces, parameterized through orthogonal geodesics. In the rest of the thesis lies the author’s attempt to persuade readers that DOGs are both useful and interesting, while developing relevant mathematical theory and a set of computational tools for modeling DOGs.
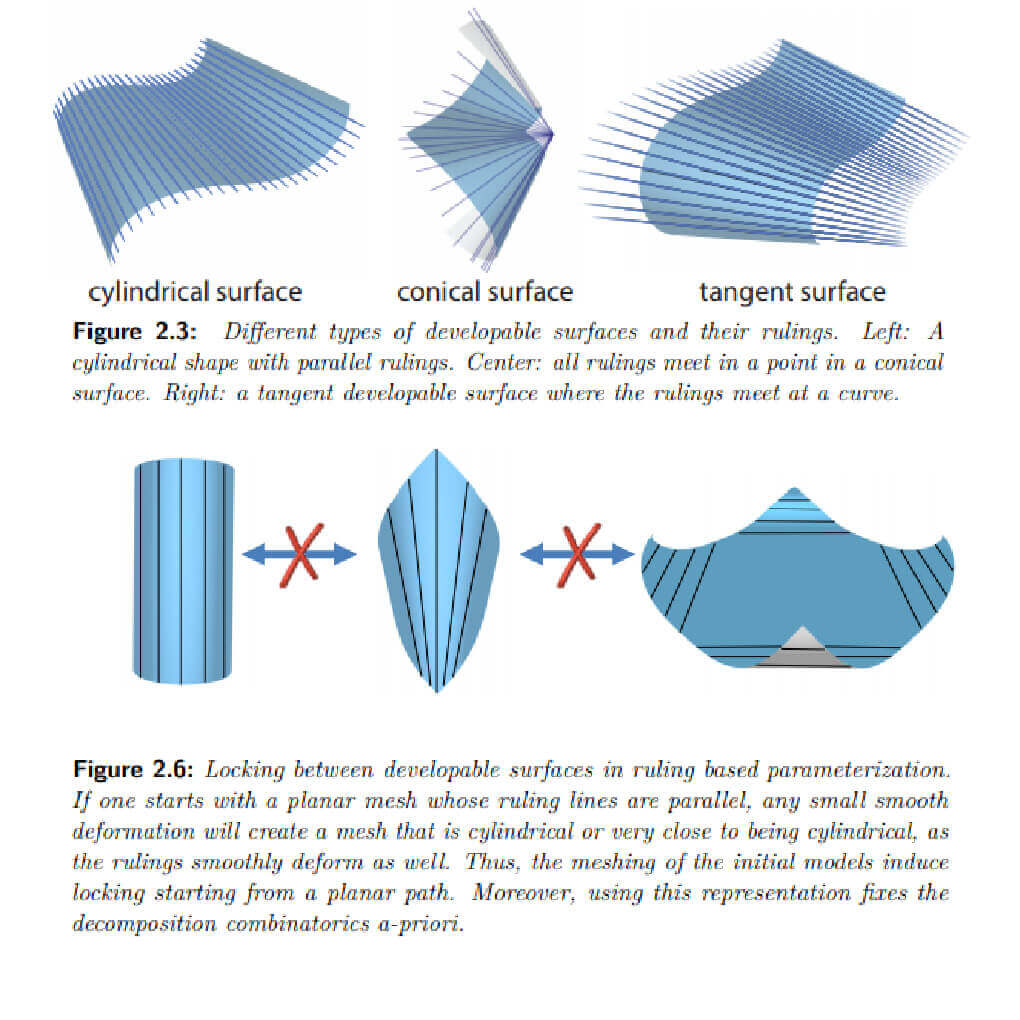 Imagine holding a planar sheet. You can roll it into a cylinder, bend it into a cone, and deform it to a variety of other shapes. As long as one does not stretch the surface, the generated shape is said to be isometric to the planar surface. Such shapes are said to be developable, because one can develop them onto the plane.
Imagine holding a planar sheet. You can roll it into a cylinder, bend it into a cone, and deform it to a variety of other shapes. As long as one does not stretch the surface, the generated shape is said to be isometric to the planar surface. Such shapes are said to be developable, because one can develop them onto the plane.
 A developable surface is difficult to design since its geometry is highly constrained; at the same time it also admits a rich set of extrinsic and intrinsic deformations. Applying standard modeling tools such as freeform space deformations or elastic surface-based bending quickly violates the developability property (local isometry to the plane). Consequently, the design of freeform developable surfaces has been an active research topic in computer graphics, computer aided design and computational origami for several decades.
A developable surface is difficult to design since its geometry is highly constrained; at the same time it also admits a rich set of extrinsic and intrinsic deformations. Applying standard modeling tools such as freeform space deformations or elastic surface-based bending quickly violates the developability property (local isometry to the plane). Consequently, the design of freeform developable surfaces has been an active research topic in computer graphics, computer aided design and computational origami for several decades.
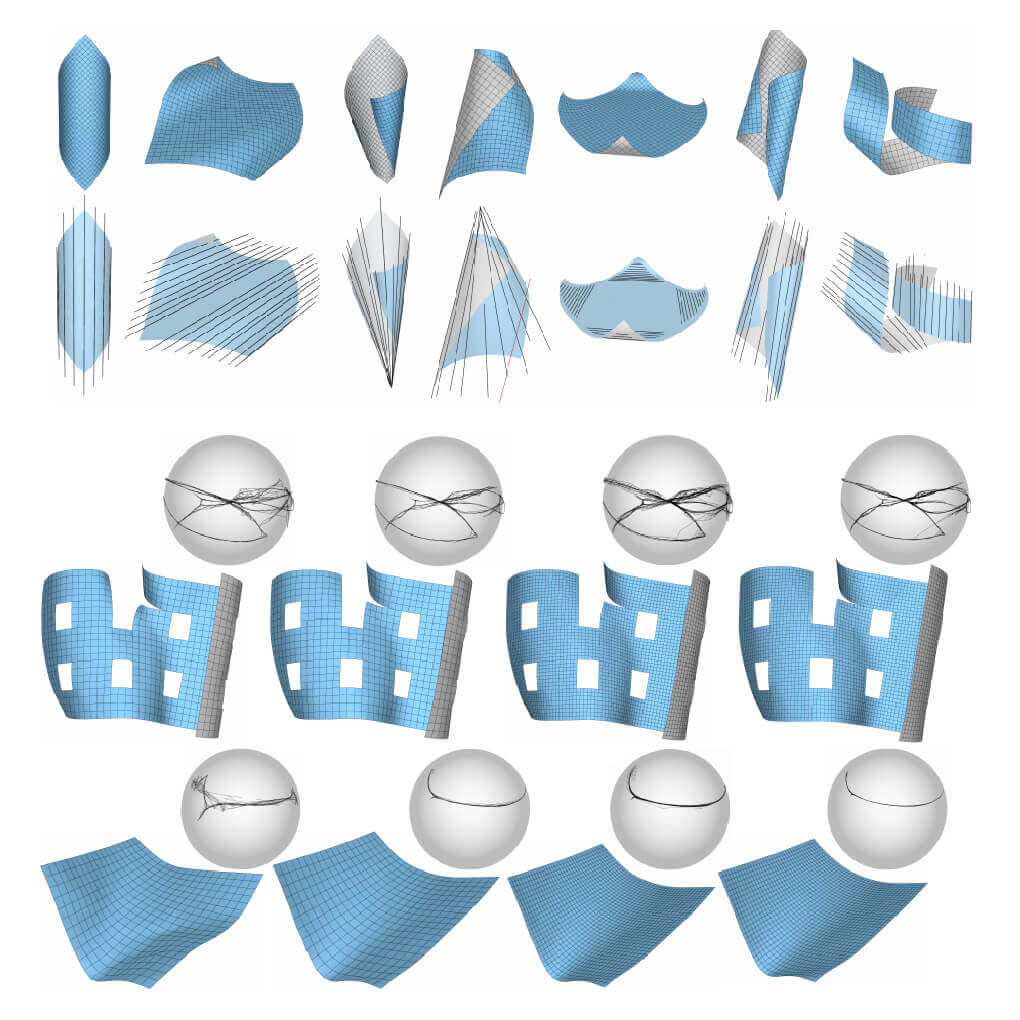 A precise discrete model is one that does not only converge in some smooth limit to its smooth counterpart, but also one that behaves well as a discrete object. In practice, one often works with a limited set of resources and a good discrete model has similar behavior and structure to its smooth counterpart, even on a rather coarse mesh. The problem of locking in various models of discrete developable surfaces can be addressed from that angle.
A precise discrete model is one that does not only converge in some smooth limit to its smooth counterpart, but also one that behaves well as a discrete object. In practice, one often works with a limited set of resources and a good discrete model has similar behavior and structure to its smooth counterpart, even on a rather coarse mesh. The problem of locking in various models of discrete developable surfaces can be addressed from that angle.
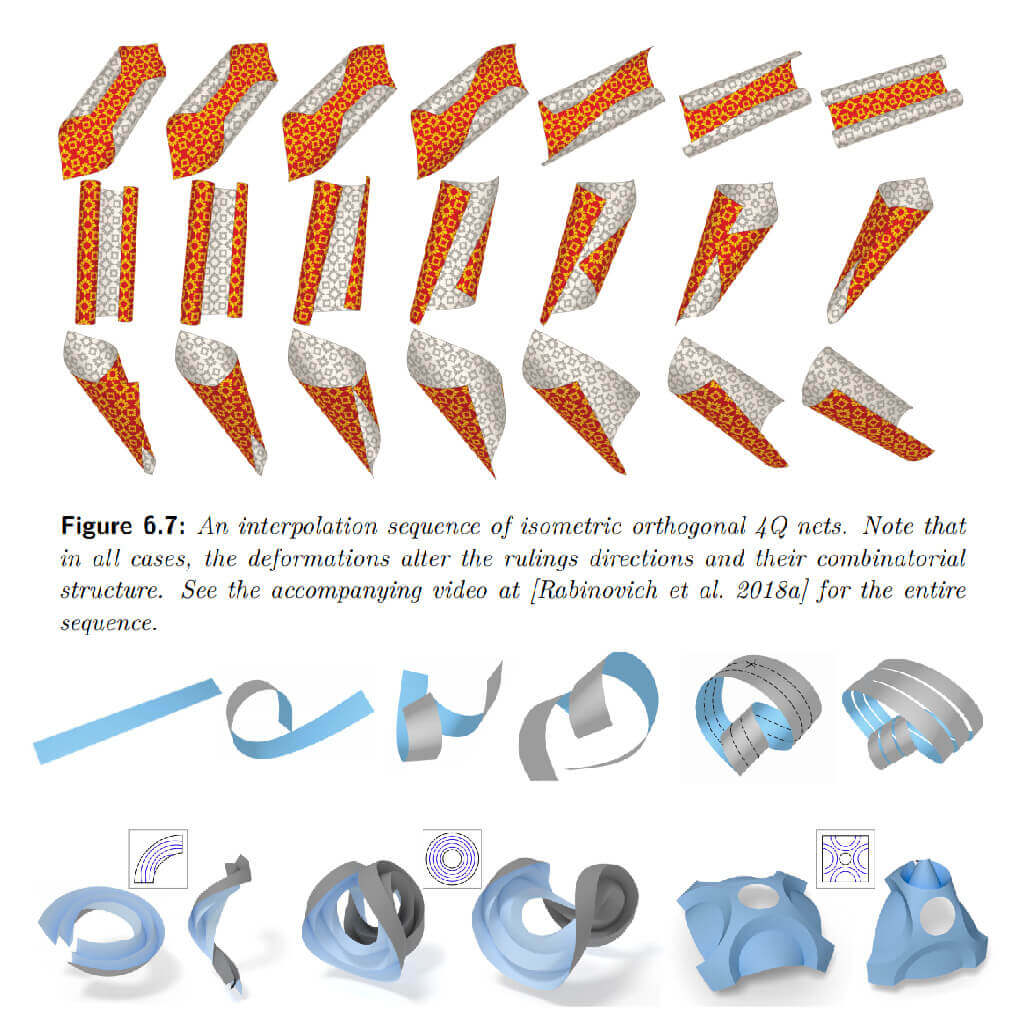 A model that is amenable to optimization is one that is simple and can be plugged into a well defined and well behaved optimization problem. Simplicity is crucial from both a practical implementation side, but also theoretically. It it often a necessity if one wants to fully understand an optimization problem and to have some practical guarantees, for instance on the existence of a solution for a given problem.
A model that is amenable to optimization is one that is simple and can be plugged into a well defined and well behaved optimization problem. Simplicity is crucial from both a practical implementation side, but also theoretically. It it often a necessity if one wants to fully understand an optimization problem and to have some practical guarantees, for instance on the existence of a solution for a given problem.
 A planar sheet can be smoothly and isometrically deformed into a variety of shapes. In such an isometric deformation, length of curves are preserved as well as angles between different curves.
A planar sheet can be smoothly and isometrically deformed into a variety of shapes. In such an isometric deformation, length of curves are preserved as well as angles between different curves.
 While a geometer represents a smooth surface with a net, a computer scientist often use a mesh to represent a discrete surface. The two are intimately linked and in both cases one can represent the same geometry using different nets or meshes.
While a geometer represents a smooth surface with a net, a computer scientist often use a mesh to represent a discrete surface. The two are intimately linked and in both cases one can represent the same geometry using different nets or meshes.
 Any smooth orthogonal geodesic net is a developable surface and can therefore be isometrically flattened to an orthogonal grid on the plane. If one considers isometry as exact preservation of edge lengths then this property doesn’t hold exactly in most DOGs, but as we will see it does hold at the smooth limit.
Any smooth orthogonal geodesic net is a developable surface and can therefore be isometrically flattened to an orthogonal grid on the plane. If one considers isometry as exact preservation of edge lengths then this property doesn’t hold exactly in most DOGs, but as we will see it does hold at the smooth limit.
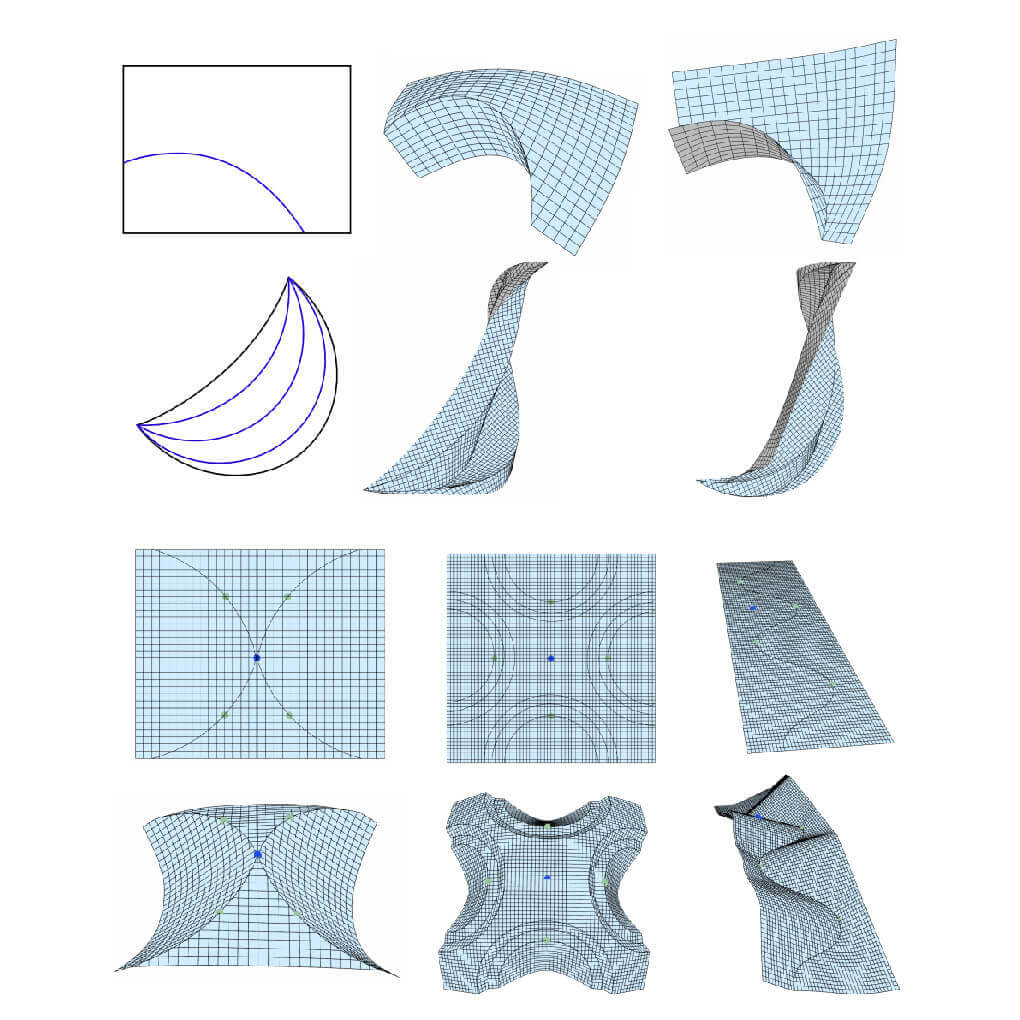 On a smooth developable surface, the rulings are global, in the sense that they either extend infinitely, or their endpoints must hit the boundaries of the surface [Spivak 1999]. Flipping this point of view, one can ask how to extend a developable surface at its boundary: the possibilities are generally quite limited, since the points along the rulings are uniquely determined. Note that arbitrarily extending rulings often results in singularities.
On a smooth developable surface, the rulings are global, in the sense that they either extend infinitely, or their endpoints must hit the boundaries of the surface [Spivak 1999]. Flipping this point of view, one can ask how to extend a developable surface at its boundary: the possibilities are generally quite limited, since the points along the rulings are uniquely determined. Note that arbitrarily extending rulings often results in singularities.
 Shape space exploration is a framework for treating shapes in the setting of Riemannian geometry, where surfaces are seen as points in a high dimensional space endowed with a metric. The work of [Kilian et al. 2007] investigated the space of triangulated surfaces, computing an as-isometric-as-possible interpolation as a geodesic between two meshes w.r.t a Riemannian metric that measures stretch of triangle edges.
Shape space exploration is a framework for treating shapes in the setting of Riemannian geometry, where surfaces are seen as points in a high dimensional space endowed with a metric. The work of [Kilian et al. 2007] investigated the space of triangulated surfaces, computing an as-isometric-as-possible interpolation as a geodesic between two meshes w.r.t a Riemannian metric that measures stretch of triangle edges.



























Comments