Shape-shifting Structured Lattices via Multimaterial 4D Printing

J. William Boley^a,b,c,1, Wim M. van Rees^b,d,1, Charles Lissandrello^e, Mark N. Horenstein^f, Ryan L. Truby^b,c, Arda Kotikian^b,c, Jennifer A. Lewis^b,c,2, and L. Mahadevan^b,g,h,i,2

^aDepartment of Mechanical Engineering, Boston University, Boston, MA 02215;

^bPaulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA 02138;

^cWyss Institute for Biologically Inspired Engineering, Harvard University, Cambridge, MA 02138;

^dDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139;

^eBiological Microsystems, Charles Stark Draper Laboratory, Cambridge, MA 02139;

^fDepartment of Electrical and Computer Engineering, Boston University, Boston, MA 02215;

^gDepartment of Physics, Harvard University, Cambridge, MA 02138;

^hDepartment of Organismic and Evolutionary Biology, Harvard University, Cambridge, MA 02138;

ⁱKavli Institute for Nano-bio Science and Technology, Harvard University, Cambridge, MA 02138

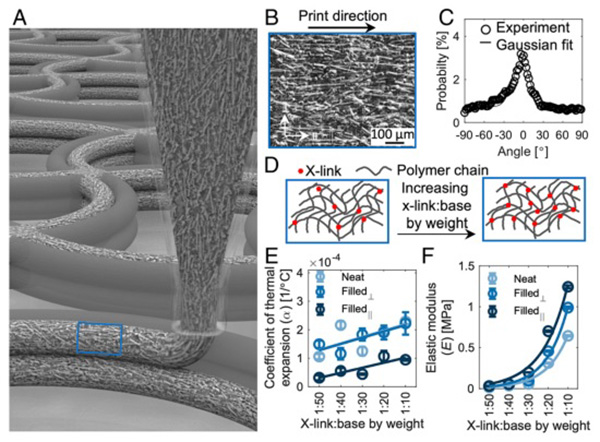
Fig. 1. Printable elastomeric inks with tailored α and E. (A) Schematic of a multimaterial 4D printing lattice structure, with ribs depicted as being 2 filaments wide and 2 filaments tall. (B) Micrograph of printed fiber-filled filament showing alignment of glass fibers, where k corresponds to the print direction and ⊥ is perpendicular to the print direction. (C) Resulting alignment probability density from B showing that the glass fibers align with the print direction, where a 0° angle corresponds to k. (D) Schematic illustrating varying of x-link to base ratio by weight (x-link:base by weight) for the elastomer matrix. (E) Measured α for different ink formulations as a function of x-link:base by weight. Lines represent linear fits to experimental data of the corresponding color. (F) Measured E of different ink formulations as a function of x-link:base by weight. Lines represent exponential fits to experimental data of corresponding color.

Shape-morphing structured materials have the ability to transform a range of applications. However, their design and fabrication remain challenging due to the difficulty of controlling the underlying metric tensor in space and time. Here, we exploit a combination of multiple materials, geometry, and 4-dimensional (4D) printing to create structured heterogeneous lattices that overcome this problem.

Our printable inks are composed of elastomeric matrices with tunable cross-link density and anisotropic filler that enable precise control of their elastic modulus (E) and coefficient of thermal expansion (α). The inks are printed in the form of lattices with curved bilayer ribs whose geometry is individually programmed to achieve local control over the metric tensor.

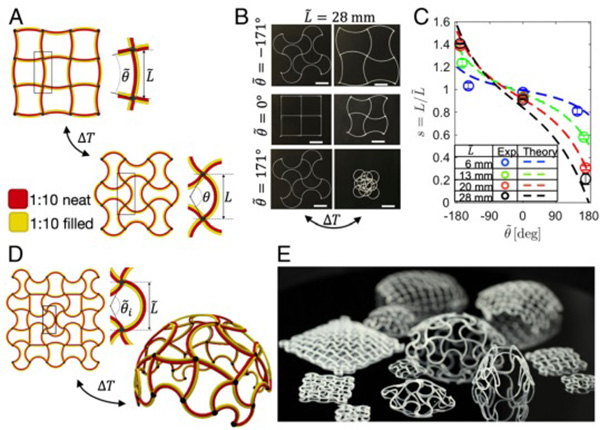
Fig. 2. Multimaterial 4D printing of homogeneous and heterogeneous lattices. (A) Schematic of bilayer lattice with defined parameters: printed lattice spacing ð~LÞ and arc angle ð~θÞ and morphed lattice spacing ðLÞ and arc angle ðθÞ after applied temperature field ðΔTÞ. (B) Images of 2D lattices as printed (Left) and after applying a ΔT of −250 °C (Right). (Scale bar, 20 mm.) (C) Linear growth factor of various printed lattices and their comparison with theory (Eq. 2) after applying a ΔT of −250 °C. (D) Schematic of a 2D heterogeneous lattice design that morphs into a spherical cap under an applied ΔT. (E) Photograph of various printed lattices after morphing into spherical caps.

For independent control of extrinsic curvature, we created multiplexed bilayer ribs composed of 4 materials, which enables us to encode a wide range of 3-dimensional (3D) shape changes in response to temperature. As exemplars, we designed and printed planar lattices that morph into frequency-shifting antennae and a human face, demonstrating functionality and geometric complexity, respectively.

Our inverse geometric design and multimaterial 4D printing method can be readily extended to other stimuli-responsive materials and different 2-dimensional (2D) and 3D cell designs to create scalable, reversible, shape-shifting structures with unprecedented complexity.

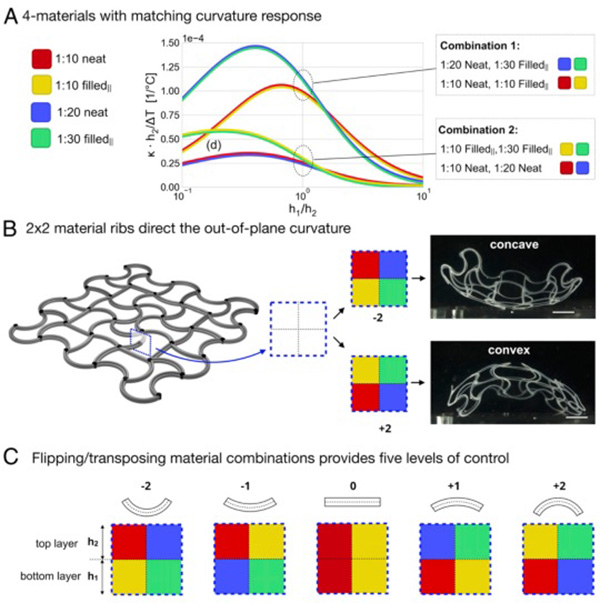
Fig. 3. Multiplex bilayer lattices via multimaterial 4D printing. (A) Dimensionless bilayer curvature increments for the 4 different bilayer material combinations. The materials are chosen so that adjacent pairs of equal thicknesses achieve approximately matching curvature increments. While in-plane curvature of each rib is governed by the left–right material pairs and the in-plane opening angle as described in the text and SI Appendix, Fig. S5, the out-of-plane curvature of each rib is governed by the top–bottom material pairs according to the graph. (B) Schematic of the multiplex bilayer lattice highlighting the cross-section of a rib and 2 experimental examples of 4D printed 4-material hemispherical lattices with maximum concave (Upper) and maximum convex (Lower) multiplex cross-sections. (Scale bars, 10 mm.) (C) Schematics of all possible material combinations for such a cross-section. With 2 materials, the lattice has a symmetric cross-section and 0 mean curvature (labeled 0). Adding 2 more materials enables us to achieve 4 different combinations of out-of-plane curvature ranging from maximum concave (labeled −2) to maximum convex (labeled +2).

Shape-morphing structured systems are increasingly seen in a range of applications from deployable systems and dynamic optics to soft robotics and frequency-shifting antennae, and they have led to numerous advances in their design and fabrication using various 3-dimensional (3D) and 4-dimensional (4D) printing techniques.

However, to truly unleash the potential of these methods, we need to be able to program arbitrary shapes in 3 dimensions (i.e., control the metric tensor at every point in space and time), thus defining how lengths and angles change everywhere. For thin sheets, with in-plane dimensions that are much larger than the thickness, this is mathematically equivalent to specifying the first and second fundamental forms of the middle surface.

These quadratic forms describe the relation between material points in the tangent plane and the embedding of the middle surface in 3 dimensions and thus, control both the intrinsic and extrinsic curvature of the resulting surface. From a physical perspective, arbitrary control of the shape of a sheet requires the design of material systems that can expand or contract in response to stimuli, such as temperature, humidity, pH, etc., with the capacity to generate and control large in-plane growth gradients combined with differential growth through the sheet thickness.

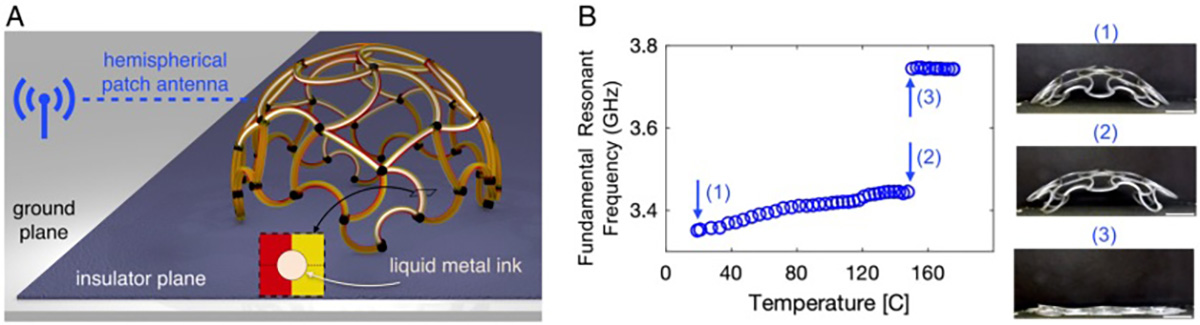
Fig. 4. Shape-shifting patch antenna. (A) Schematic of experimental setup for a spherical cap lattice innervated with a liquid metal ink, which is used as a shape-shifting patch antenna. (B) Resonant frequency of a printed patch antenna at various temperatures (Left) and side view images of the antenna corresponding to different resonant frequencies (Right). Parameters for all lattices are as follows: low α material is 1:10 filledk, high α material is 1:10 neat, and t1 =t2 =0.4 mm. (Scale bars, 10 mm.)

Such systems are difficult to achieve experimentally; hence, most current shape-shifting structures solutions rarely offer independent control of mean and Gaussian curvatures. We address this challenge by 4D printing a lattice design composed of multiple materials.

Beginning at the material level, we created printable inks based on a poly(dimethylsiloxane) (PDMS) matrix, an elastomeric thermoset that exhibits a large operating temperature window and a high thermal expansion coefficient. Although the inks are printed at room temperature, the broad range of polymerization temperatures for PDMS enables us to cure the resulting structures at much higher temperatures.

On cooling to room temperature, these cured matrices achieve maximal contraction, hence transforming into their deployed states. The same base elastomer is used in all inks to facilitate molecular bonding between adjacent ribs and layers. To create inks with reduced thermal expansivity, we fill the elastomer matrix with short glass fibers (20% wt/wt) that preferentially shear align along the print path.

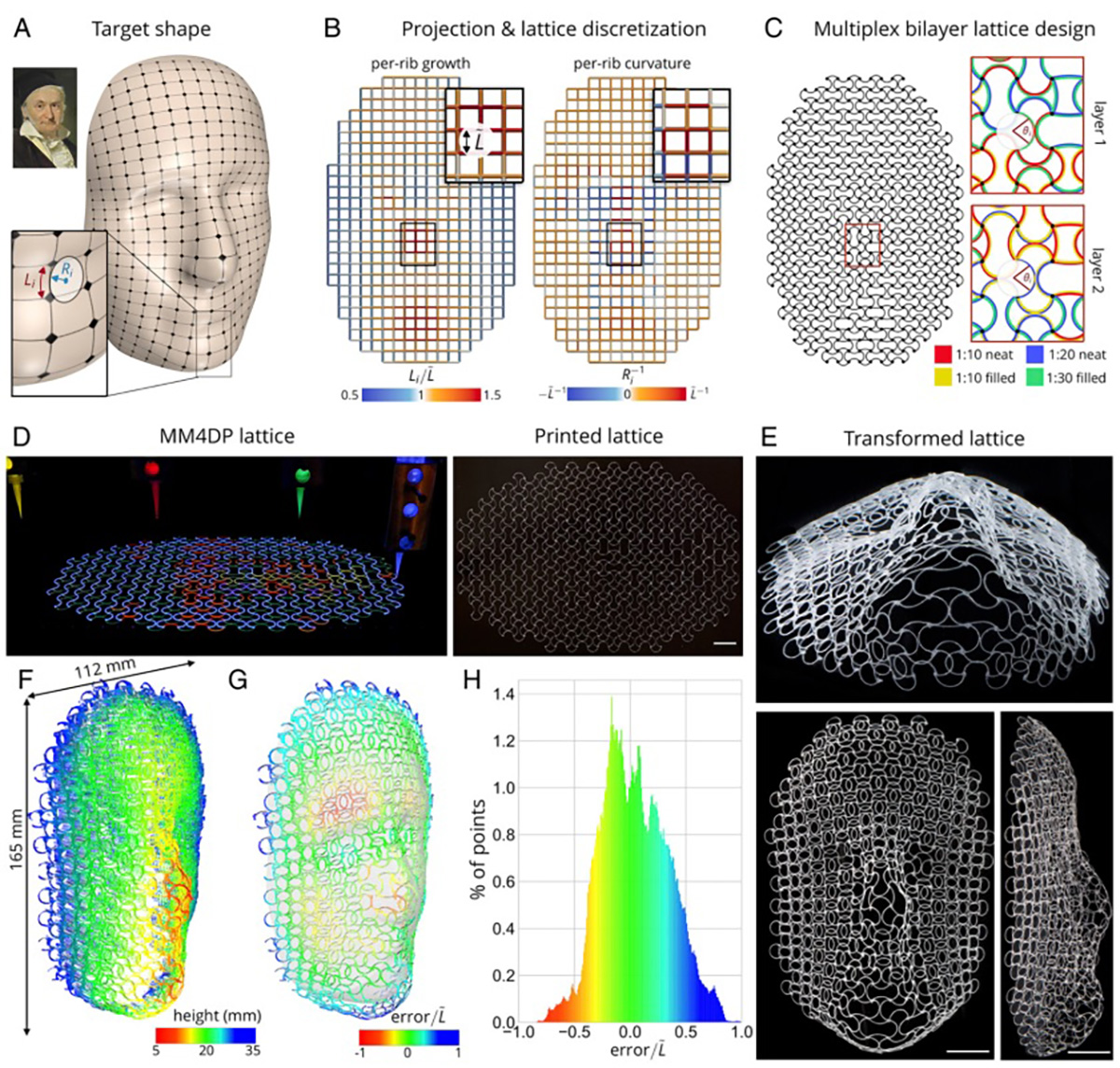
Fig. 5. Integrated design and fabrication of a complex geometrical shape. (A) Process for creating a 3D face as the target shape: begin with a 2D image of Carl Friedrich Gauss’s likeness (Upper Left) and generate a 3D surface (the target shape) via an artificial intelligence algorithm. The detailed view highlights the target length ðLiÞ and normal radius of curvature ðRiÞfor 1 specific rib. (B) Conformally mapped and discretized lattice with resulting local rib growth ðLi=~LÞ and normal curvature ðR−1 i Þ, where ~L=10 mm. (C) Programmed multiplex bilayer lattice for printing. Detailed views show a sample area of the programmed lattice, with first and second layers of the lattice showing prescribed ~θi and multiplex materials. (D) Photographs of lattice during (Left) and after (Right) printing. MM4DP, multimaterial 4D printing. (Note that fluorophores are incorporated in each ink to highlight multimaterial printing.) (Scale bar, 20 mm.) (E) Photographs of lattice after transformation. Perspective view (Upper), top view (Lower Left), and side view (Lower Right) of transformed lattice. ΔT =−250 °C. (Scale bars, 20 mm.) (F) A 3D scan of the transformed face. (G) Normalized error ðerror=~LÞ of the 3D scan superimposed onto target shape. Negative values represent points that lie below target shape surface. Positive values represent points that lie above target shape surface. (H) Distribution of normalized error.

Thin shape-shifting structures are often limited in their ability to morph into complex and doubly curved shapes. Such transformations require both large in-plane expansion or contraction gradients and control over extrinsic curvature, which are hard to achieve with single materials arranged in simple architectures.

We solve this problem by 4-dimensional printing of multiple materials in heterogeneous lattice designs. Our material system provides a platform that achieves in-plane growth and out-of-plane curvature control for 4-material bilayer ribs. The lattice design converts this into large growth gradients, which lead to complex, predictable 3-dimensional (3D) shape changes. We demonstrate this approach with a hemispherical antenna that shifts resonant frequency as it changes shape and a flat lattice that transforms into a 3D human face.