Parameterization and Tiling of Polyhedral Surfaces
Polyhedral Surfaces
Dipl.-Math. Techn. Matthias Nieser
February 2012
 Polyhedral surfaces are probably the most common representation for surfaces in computer graphics. Because of their simplicity, they can be processed very efficiently in modern computers and graphics cards.
Polyhedral surfaces are probably the most common representation for surfaces in computer graphics. Because of their simplicity, they can be processed very efficiently in modern computers and graphics cards.
 The field of discrete differential geometry investigates polyhedral surfaces from a mathematical point of view. The aim is to provide proper discrete analogs of notions and methods of the smooth differential setting, and to establish a corresponding theory. The development of a consistent theory is challenging, since arbitrary polyhedral surface meshes often lack regularity and a high-level semantic structure. In particular for triangle meshes, important surface features are often not emphasized and triangles are not adapted to the overall shape.
The field of discrete differential geometry investigates polyhedral surfaces from a mathematical point of view. The aim is to provide proper discrete analogs of notions and methods of the smooth differential setting, and to establish a corresponding theory. The development of a consistent theory is challenging, since arbitrary polyhedral surface meshes often lack regularity and a high-level semantic structure. In particular for triangle meshes, important surface features are often not emphasized and triangles are not adapted to the overall shape.
 Surface parameterization is the process of mapping a surface into the two-dimensional plane. Conceptually, the surface is considered as a distorted Euclidean plane where the parameterization describes the relation, the deformation and the differences to the plane. The parameterization equips the surface with additional structure, such as providing a metric and consistent local coordinates in all tangent spaces.
Surface parameterization is the process of mapping a surface into the two-dimensional plane. Conceptually, the surface is considered as a distorted Euclidean plane where the parameterization describes the relation, the deformation and the differences to the plane. The parameterization equips the surface with additional structure, such as providing a metric and consistent local coordinates in all tangent spaces.
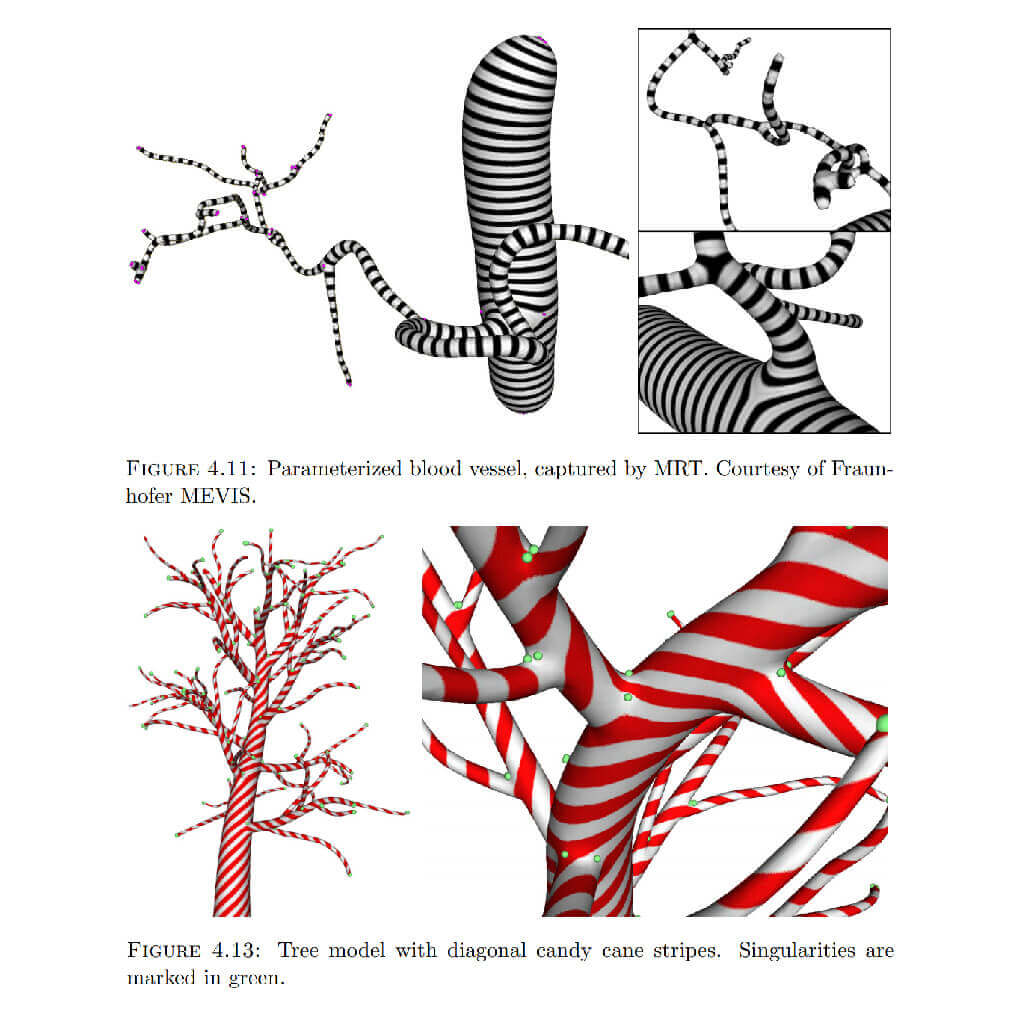 The task of generating a parameterization of high quality is challenging. Depending on the actual application, the desired properties are quite different. However, for almost all purposes, it is important to achieve low metric distortion, since then the real surface is approximated well by its image in the flat plane. Applications range from texture mapping in computer graphics and texture synthesis to remeshing and automatic construction of hierarchical subdivision surfaces. All of these applications benefit from the additional structure of a parameterization.
The task of generating a parameterization of high quality is challenging. Depending on the actual application, the desired properties are quite different. However, for almost all purposes, it is important to achieve low metric distortion, since then the real surface is approximated well by its image in the flat plane. Applications range from texture mapping in computer graphics and texture synthesis to remeshing and automatic construction of hierarchical subdivision surfaces. All of these applications benefit from the additional structure of a parameterization.
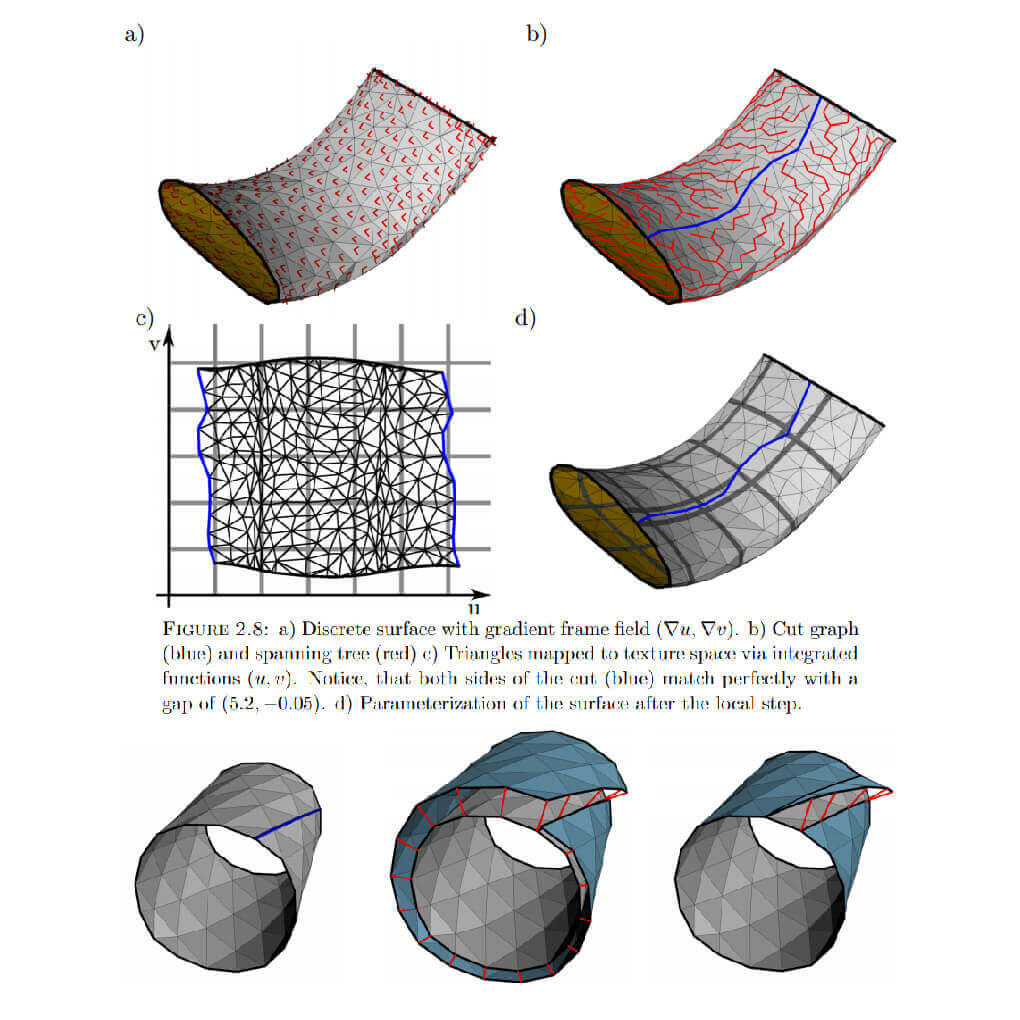 Most common surface parameterization approaches are made for quadrilateral tilings and generate a regular quadrilateral grid. In this thesis, different tilings and symmetry groups are also considered.
Most common surface parameterization approaches are made for quadrilateral tilings and generate a regular quadrilateral grid. In this thesis, different tilings and symmetry groups are also considered.
 A guiding-field-based parameterization method like QuadCover allows very specific control over the alignment of the parameterization and its metric. The automatically computed field in the first step is exchangeable by any other field provided as input. In this sense, QuadCover is a more general approach which can easily be adapted to match different user-specified criteria.
A guiding-field-based parameterization method like QuadCover allows very specific control over the alignment of the parameterization and its metric. The automatically computed field in the first step is exchangeable by any other field provided as input. In this sense, QuadCover is a more general approach which can easily be adapted to match different user-specified criteria.
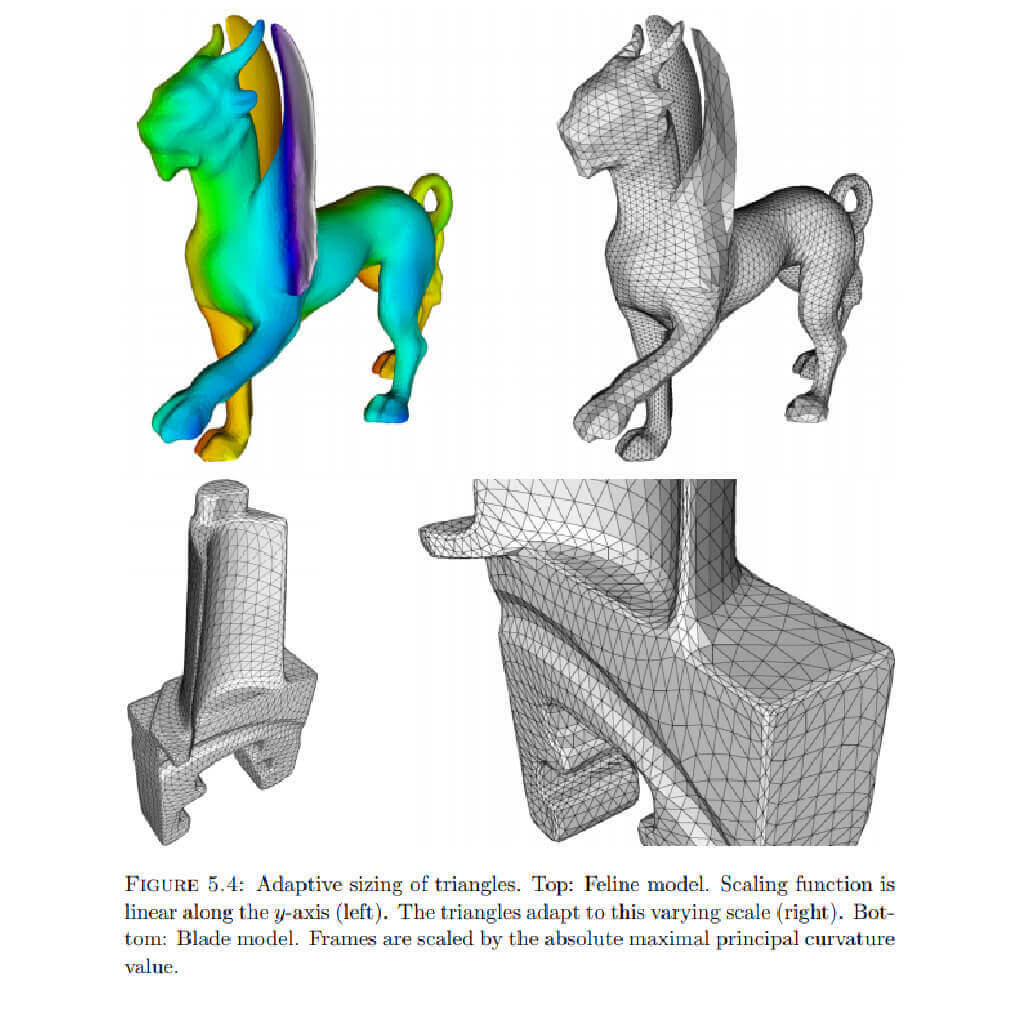
 Early approaches on vector field design specify a sparse set of vectors and interpolate them over the whole surface [Praun 2000, Turk 2001]. Further techniques give direct control over the field topology by directly specifying the location and indices of singularities [Theisel 2002, Li 2006, Zhang 2006, Fisher 2007].
Early approaches on vector field design specify a sparse set of vectors and interpolate them over the whole surface [Praun 2000, Turk 2001]. Further techniques give direct control over the field topology by directly specifying the location and indices of singularities [Theisel 2002, Li 2006, Zhang 2006, Fisher 2007].
 Vector fields can be generalized to admit different rotational symmetries. Zhang et al. concern the design of line fields that do not distinguish between forward and backward directions [Zhang 2007].
Vector fields can be generalized to admit different rotational symmetries. Zhang et al. concern the design of line fields that do not distinguish between forward and backward directions [Zhang 2007].
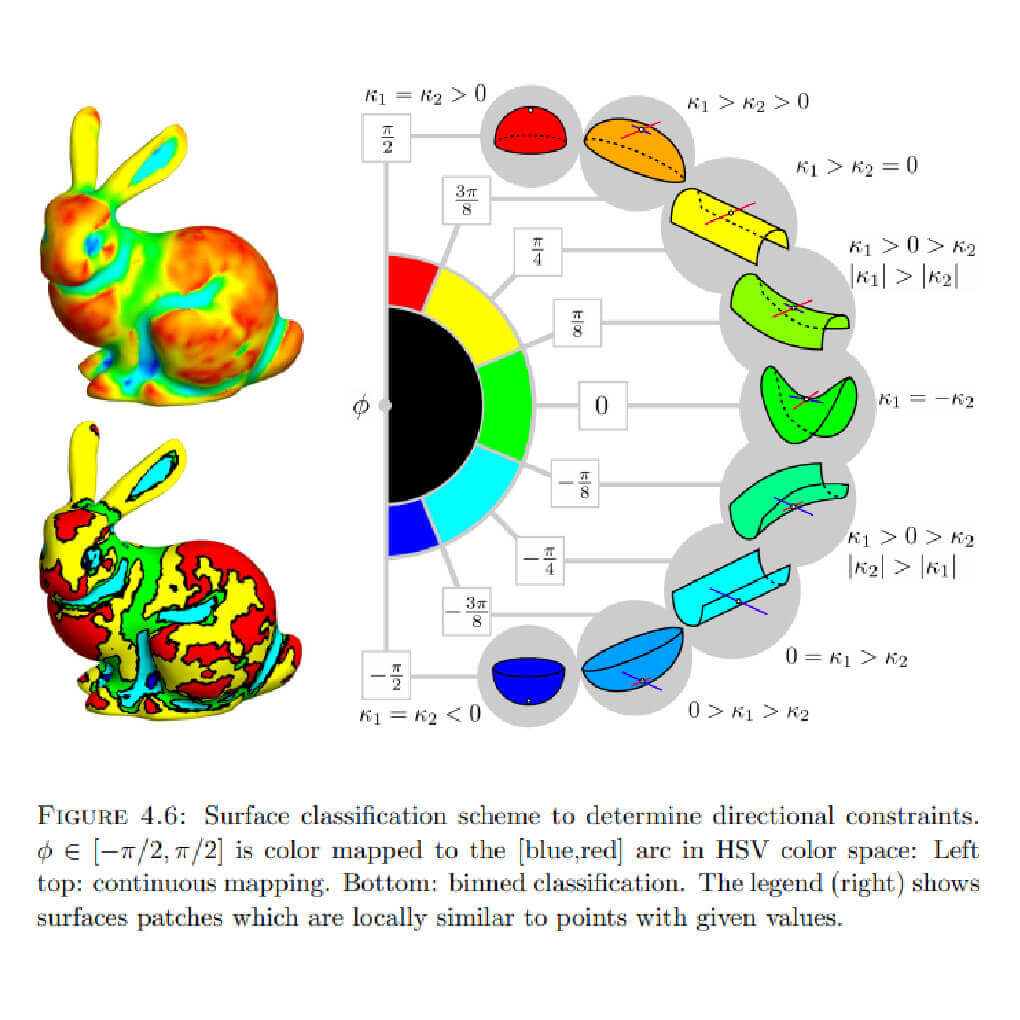
 Smooth cross fields are very stably computed by variational approaches which minimize the squared angles between vectors in adjacent triangles. Such an energy function is first proposed by Wei et al. [Wei 2001]. The MIQ algorithm [Bommes 2009] computes principal curvature directions in some trusted areas and uses a similar energy to interpolate the cross field to the whole surface. Singularities are found automatically using a mixed integer solver.
Smooth cross fields are very stably computed by variational approaches which minimize the squared angles between vectors in adjacent triangles. Such an energy function is first proposed by Wei et al. [Wei 2001]. The MIQ algorithm [Bommes 2009] computes principal curvature directions in some trusted areas and uses a similar energy to interpolate the cross field to the whole surface. Singularities are found automatically using a mixed integer solver.
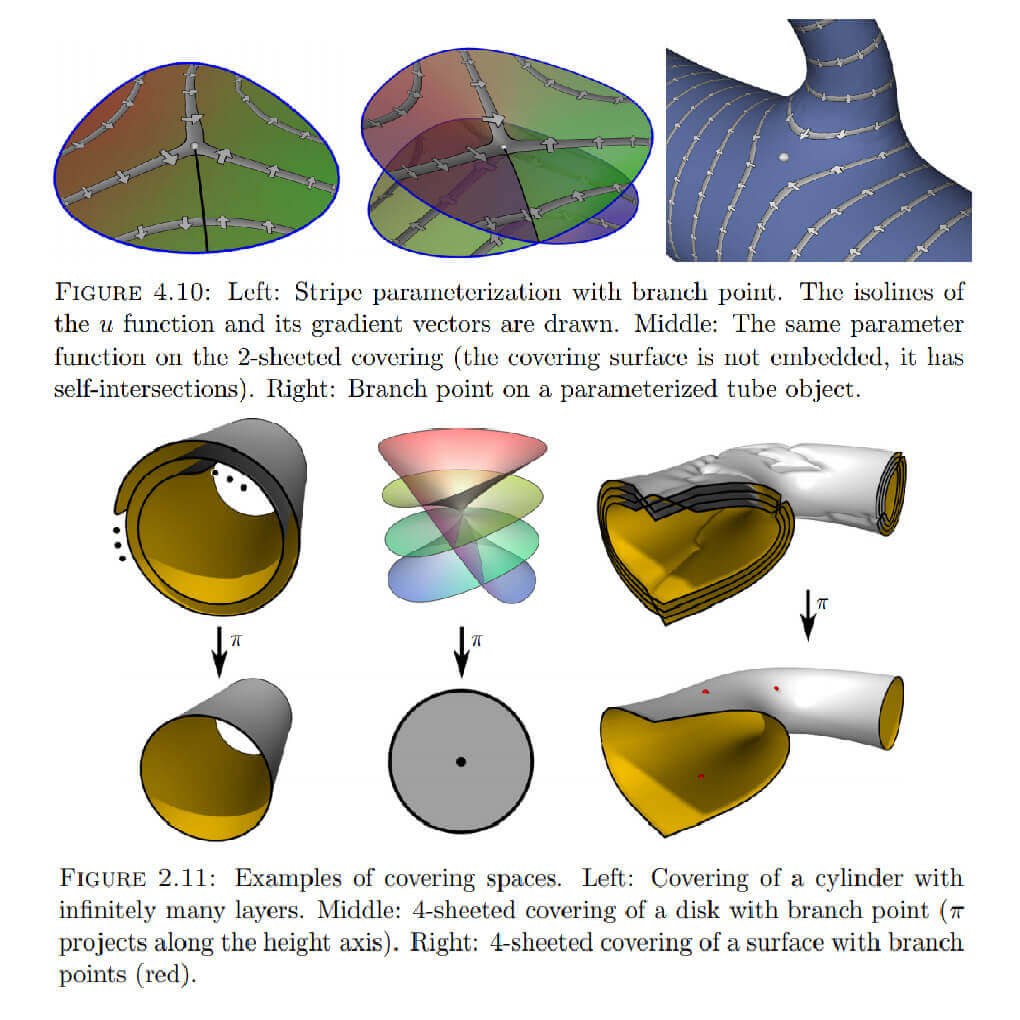 The goal of QuadCover is to construct a parameterization for a given surface. The concepts described in this section are based on a setting from differential geometry. Hereby, the underlying surface is a smooth twodimensional manifold, which is a second-countable Hausdorff space M covered by a collection of charts Mi . The charts are homeomorphic to a two-dimensional Euclidean disk and may overlap, i.e. a single point of M may be represented in several charts.
The goal of QuadCover is to construct a parameterization for a given surface. The concepts described in this section are based on a setting from differential geometry. Hereby, the underlying surface is a smooth twodimensional manifold, which is a second-countable Hausdorff space M covered by a collection of charts Mi . The charts are homeomorphic to a two-dimensional Euclidean disk and may overlap, i.e. a single point of M may be represented in several charts.



























Comments