Philosophy,Mathematics & Parametric Design
The Impact of Philosophy and Mathematics on
the Aesthetics of the Digital Architecture based on Parametric Design
National School of Architecture of Rabat, AV Ennakhil,, Rabat, Morroco

Figure 1: Side by side Sydney Opera House of Ero Saarinen with a simple curvature Cultural Center HeydAliyev of Zaha Hadid with a double curvature.
We are currently seized by the diversity and originality of contemporary architecture throughout the world, an architecture often characterized by fluid forms and non-standard realization processes. The purpose of this article is to throw light on the mathematical and philosophical foundations that have opened architecture to the hegemony of digital technologies.
We will try to explain how, originally, this mutation was co-driven, essentially, by mathematics and philosophy. Signs of this mutation date back to the late 1960s, years of the advent of the microprocessor and the discovery in mathematics of other types of non-Euclidean geometry.
Figure 2: Greg Lynn, Euclidean geometry curve at the top and Spline curve obtained by Bêzier Spline, as used by 3D modeling software (bottom). The curve at the top is composed of 9 fragments of arcs of circles whereas the curve Spline is composed of an infinity of arc. (G. Lynn, 1999).
It took about twenty years, which were necessary for the development of machines, for a handful of American architects to adopt what they agreed to as French theory of certain French philosophers to define new architectural forms. The architectural aesthetics of digital design, whose transcendental meaning is linked to its generative logic, is now subject to the hegemony of the algorithm.
The nature of this one confers to the conceptual approach of multiple appellations such as Morphogenesis, Genetic Architecture, Tectonics, fractal geometry. Deleuze was not the only philosopher to have influenced American architects by philosophical paradigms. There was before him Jacque Derrida, the French philosopher, whose famous deconstructivity theory was adopted by Piter Eisenman, Frank o Gehry, and Daniel Libeskind, and many others who adopted what is agreed as “the French theory”.
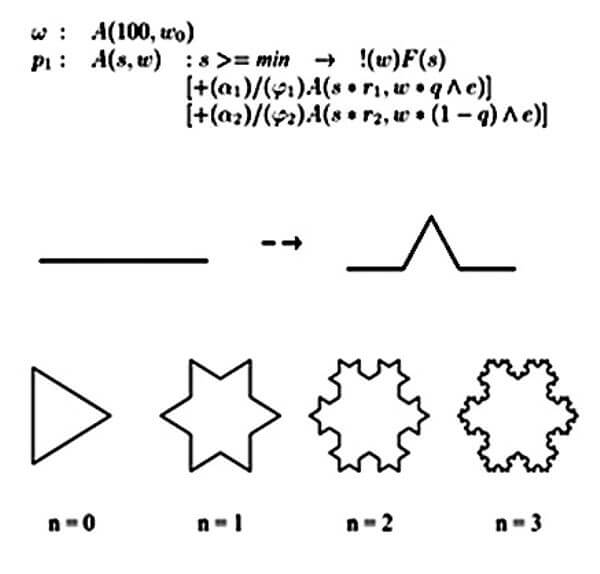
Figure 3: visual interpretation of production of the snowflake curve, and curve after n= 0, 1, 2 and 3
derivation step. (Przemyslaw Prusinkiewicz, Jim Hanan, Mark Hammel, and Radomir Mech, 2004).
They have translated this theory into highly controversial architectural expressions. In his theoretical construction, Jacque Derrida unveiled the nonscientific legitimacy of certain ways of thinking that have lost their argument in the face of social and technological changes.
In architecture, trabeation, for example, is a conceptual technique that has characterized architecture from the primitive hut, but today it is outdated with the appearance of self-compacting concrete that combines a very fluid fluidity and an impressive resistance. Thus, the principles of verticality once demanded by stability against the laws of gravity must be reconsidered.
With the de-constructivist philosophy, the window is redefined differently to assume its role of lighting and ventilation and to participate in the plasticity of the work and give birth to an architectonic whose characteristics exceed the three-dimensional qualities to add a 4th dimension which is perceived through the movements suggested by the forms.
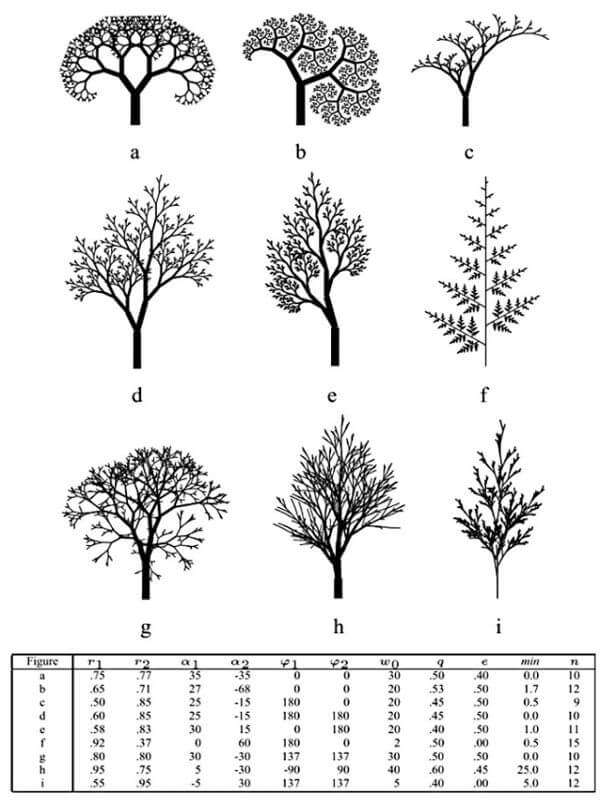
Figure 4: Simple structures generated by parametric DOL-System with different values of constants (Przemyslaw Prusinkiewicz, Jim Hanan, Mark Hammel, and Radomir Mech, 2004).
The action of investing space by giving it a meaning always pushes architects to resort to semantics and metaphors that release coded messages and interpret the intellectual and social concerns of their times. In opposition to digital architecture, which wants to be fluid and connected, the de-constructivist architecture is characterized by Conflict and Contradiction.
The use of the contrast often used to describe this architecture reduces its value and advocates that of digital which is known as “Blobs architecture”.
The contradiction and the conflict refer both to the same meaning of the opposition. The use of these semantics in architecture is motivated mainly by artistic concerns that an architectural work must meet because the realization of a work of art depends on its ability to express the contradictions that govern human functioning (Boyes, 1993).

Figure 5: Plate GARDEN. Several Context-sensitive grafted species showing the variety easily obtained. (Smith, 1984).
These aspects, to which architecture is bound to conform, are neither of a technical nature nor of a philosophical order, and they are common to many works of art spread over several streams and periods in history. One of the revolutionary characteristics brought by the digital technologies is that it has allowed the abundance of Euclidean geometry composition concepts in favor of other geometries, so-called topological and fractal, which rhyme with the spirit of the fold of Deleuze.
The adjective “fractal”, is a neologism created by Benoît Mandelbrot in 1974 from the Latin root fractus (Dehouve, 2014). Which means “broken”, “irregular”. This change in the modes of design is due to a series of reasons where the digital is only the facilitating element and where the philosophy provides the theoretical argumentation. We try to explain why this change took place and how it occurred.

Figure 6: Plate CARTOON. TREE. A–D Rendering of the
context-free grammar in the figure, (Smith, 1984).
The classical mechanisms of projections of project concepts based on Euclid’s geometry such as symmetry, centrality, repetition, rotation, etc., no longer amuse the architects. In spite of their utility, their beauty, their stability, and above all their universality, Euclid’s laws are discarded by the necessities of change and the aesthetics of “blobitecture”.
Viollet-le-Duc often said that geometry is the cousin of architecture, but it has identified another topological and fractal geometry made manageable with the artificial assistance of digital technology, as we will show below. If we attach great importance to this aspect of geometry, it is because it is at the base of the peculiarity of the architecture of the blobs. We admit that the predominance of the curve and rounded and bent angles is not peculiar to the architecture of the digital; it is present in many iconic projects well before that.
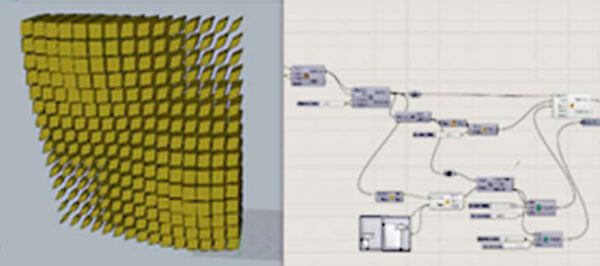
Figure 7: Scale Nu – Grasshopper Tutorial », Parametric House – Rhino Grasshopper Tutorials (blog), Of Mohamed Yazdi .
The Sydney Opera is a relevant example in this context, the project was designed by the Danish Jorn Utzon in 1957 (1957-1973) and is one of the most famous buildings of the 20th century. Digitally generated forms are neither designed nor drawn as the conventional concept would, but they are obtained by generative calculation methods that are chosen by the designer.
Thus, instead of modeling an external form, designers articulate an internal generative logic, which then automatically produces a range of possibilities from which to choose a formal proposition appropriate for further development. This is one of the possibilities offered today by the machine, and which remains the most original and the most revealing of the important changes taking place in Architecture. We are now talking about computational design or the role of the algorithm that goes beyond the representation of virtual reality thought but participates in its manufacture.

Figure 8: The infinite variability of mass Parametric Design- Rhino Grasshopper Tutorials (blog), Of Mohamed Yazdi.
To understand how this was established in architecture, we must go One year before the invention of the microprocessor by an engineer and a physicist of Intel: Marcian Hoff and Federico Faggin (Binet, 2003); a Hungarian biologist named Aristid Lindenmayer (1925-1989) introduced a formalism in 1968 simulate the development of multicellular organisms (Kolarevic, 2003), which was later called L-Systems (Lindenmayer, 1968).




























Comments