Programmatic Design Methods in Architecture
(GA+TRIZ Solution Search Method)

Anahita Khodadadi
A dissertation submitted in partial fulfillment of the requirements for the degree of
Doctor of Philosophy (Architecture)
in The University of Michigan, 2019

When an architectural design problem is stated, it may take several iterations to evaluate the design alternatives, modify the problem statement and the corresponding solutions and make the final decision. The recursive essence of an architectural design procedure and the designer’s tendency to explore further possibilities increases the use of iterative programming search methods to find suitable solutions.

Although there have been successful accomplishments in parametric modeling and evolutionary form exploration methods, the prior step of problem structuring has been developed less. We can still solve the wrong problem correctly. Thus, the step of problem structuring has significant effect on the final design outcome. A common challenge in the application of computational design methodology is to discern the parameters that influence the project outcome.

Sometimes the solution may be found around a design parameter that is not included in the parametric model and form exploration procedure. This challenge is more likely when contradictory design objectives exist in a project. Then, the designer may favor one design criterion over the others, or compromise (trade-off) and choose a solution among a group of suitable ones.

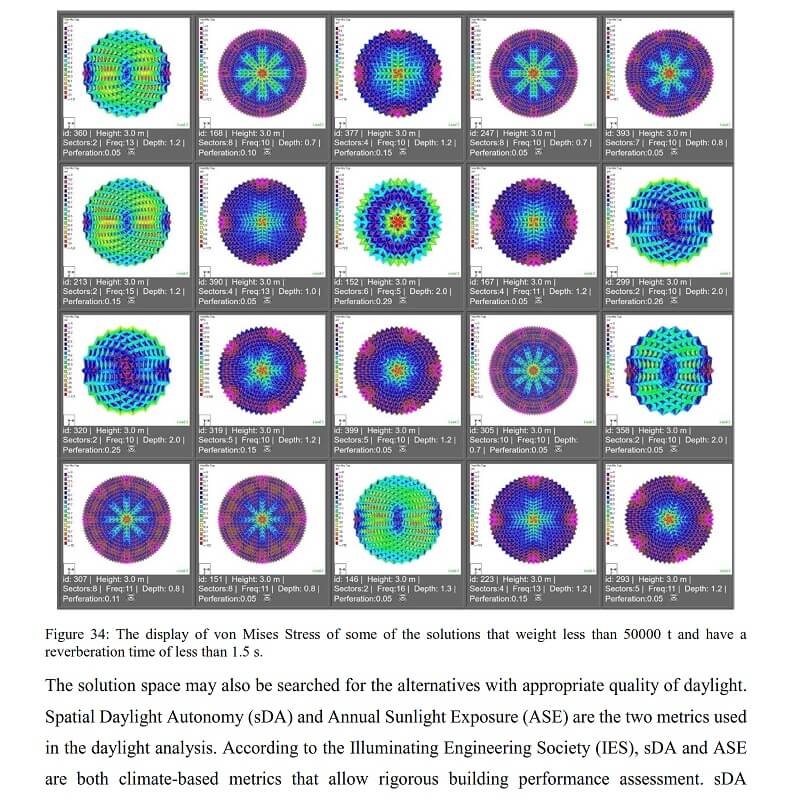
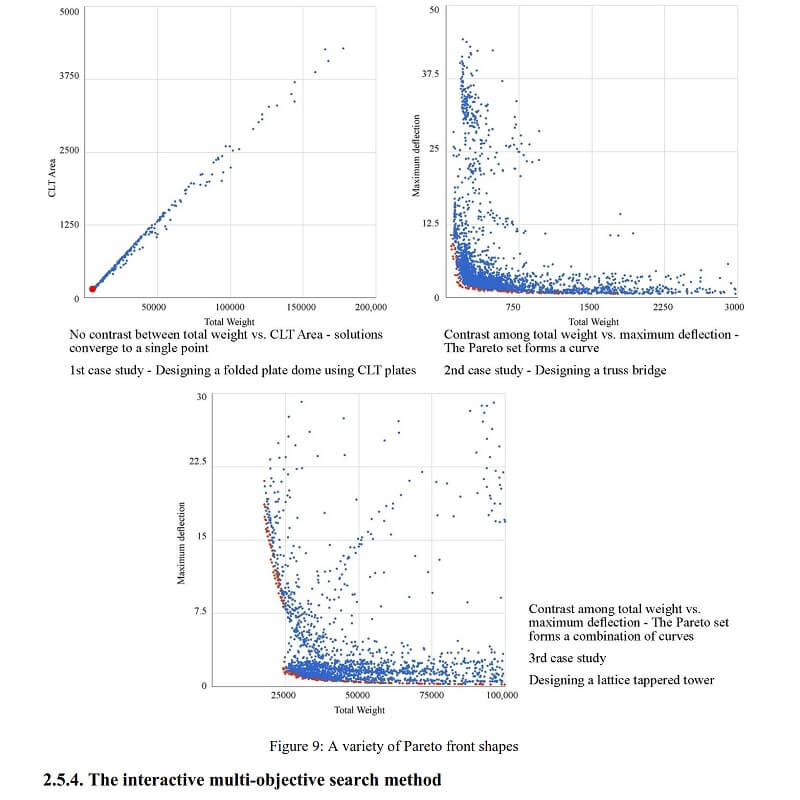
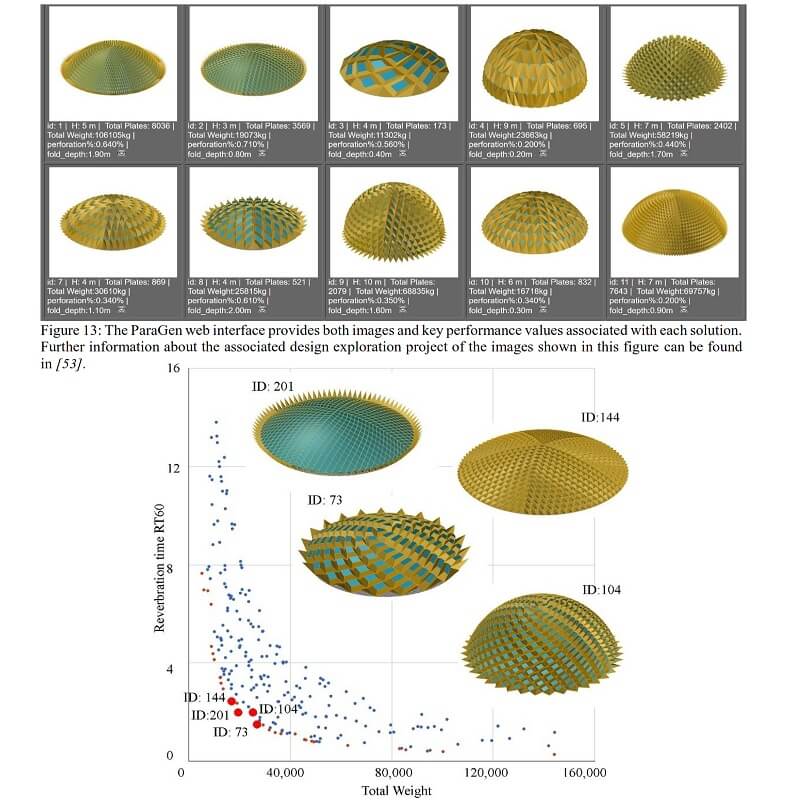
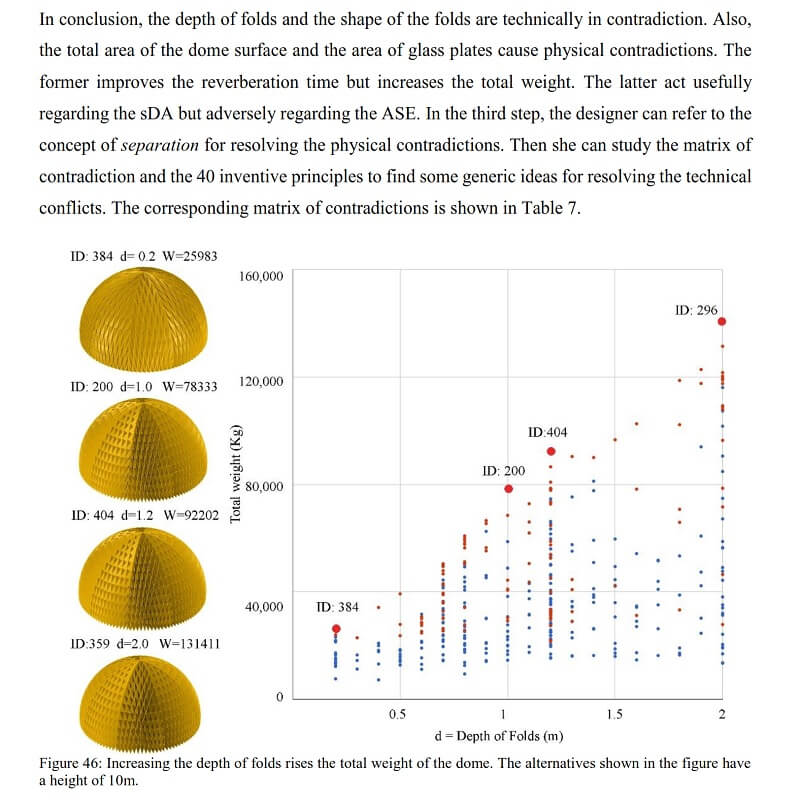
In such cases, the corresponding Pareto front may be studied to find the best trade-off solutions between two or more performative design objectives. A third approach can be the attempt to eliminate the contradiction innovatively. Accordingly, the designer may apply data mining techniques or clustering and classification algorithms to achieve higher-level information or implicit search goals to make a final decision.

In this dissertation by Anahita Khodadadi, author intends to introduce a design search method that a designer unspecialized in the field of data mining can understand and employ in both the formulation of a design problem and in the exploration of generated solutions. The main goal of this dissertation is to introduce a method which provides better problem structuring and decision making.

This computational search method is expected to provide the benefits of the application of a genetic algorithm (GA) and the Theory of Inventive Problem Solving (TRIZ) at the same time. The TRIZ Inventive Principles and the associated Matrix of Contradiction are combined with a Non-Destructive Dynamic Population Genetic Algorithm (NDDP GA) used in the ParaGen method, initially developed by Peter von Buelow, to develop the GA+TRIZ method.

The GA+TRIZ method helps the designer build a better parametric model where pertinent variables, not all possible ones but those which will more probably be dominant, are included. Furthermore, following the map of the GA+TRIZ design method can provide higher- level information which is useful in making better decisions when conflicting design objectives exist.

To examine the suitability and benefits of the application of the GA+TRIZ search method, four design case studies are carried out using the GA+TRIZ map of work. The cases are chosen from design explorations previously solved using only the ParaGen method. In each design case, the design process and the outcome of the explorations are compared with the corresponding results from in the previous trials with the ParaGen-only procedure.

The following four metrics are used to evaluate the application of the GA+TRIZ method:

• Diversity and particularity of solutions
• Performative cost
• Time efficiency
• The amount of data provided for decision making

The outcome of this research is the description of the GA+TRIZ search method along with examples of its application and all the required codes, scripts, and components.