Rationalizing Curved Folding

Designing One-DOF Mechanisms for Architecture by Rationalizing Curved Folding

Tomohiro TACHI¹, Gregory EPPS²

¹Graduate School of Arts and Sciences, The University of Tokyo 3-8-1 Komaba, Meguro-Ku, Tokyo, 153-8902, JAPAN

²RoboFold Ltd London, SW18 2LR, UK

Fig. 1: A car model by Gregory Epps animated by Rigid Origami Simulator, using the rulings reconstruction by Killian et al.

We propose a modeling method based on rationalizing curved folding in order to find the form variations of 1DOF origami mechanism. We interact with a physical paper model of curved folding and then discretize a curved folding by identifying and fixing the rulings.

Fig. 2: A car model by Gregory Epps.

The discretized form is a rigid origami structure with at most one degree of freedom. The form adjustment follows the discretization so that it is sure to realize a mechanism. The workshop performed by the authors based on the proposed design method is reported.

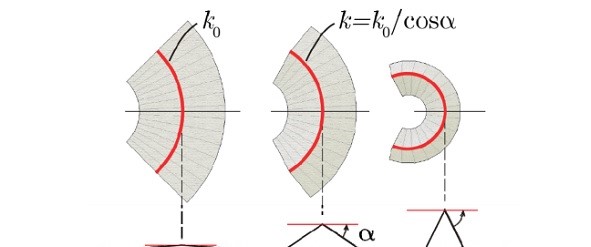
Fig. 3: Pattern-3D Relation 1: Curvature and fold angle.

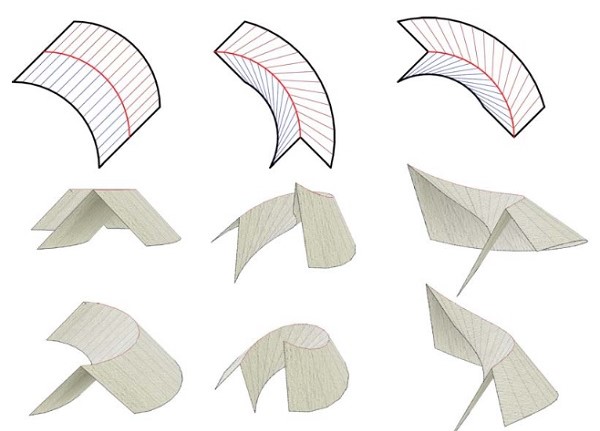
Fig. 4: Pattern-3D Relation 2: Rulings and twisting. Left: Non-twisting curved folding by straight rulings alignment in the crease pattern. Middle & Right: Twisting curved folding by kinked rulings alignment.

The objective of the workshop was to utilize the 1DOF characteristic of discretized curved folds as a constraint in the design of dynamic architectural components. The results showed the feasibility of the method and suggested a novel methodology for designing.

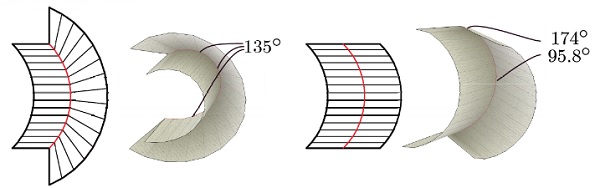
Fig. 5: Pattern-3D Relation 3: Uniform and non-uniform folding. Left: Uniform angle folding using mirror reflecting rulings. Right: Non-uniform folding (generic). The folding angle is not constant along the crease.

Fig. 6: Curved folding design using mirror reflection of a developable surface (a more elaborate design example is Huffman’s cone design).

Kinetic design in architecture is very important, e.g., dynamic solar shading, doors and openings, acoustic controllers, or portable furniture; virtually any architecture has kinetic components to be functional.

However, the design of such components is morphologically poorly investigated field. This can be attributed in part due the challenge imposed by an extra dimension (time) apparent in the component design.

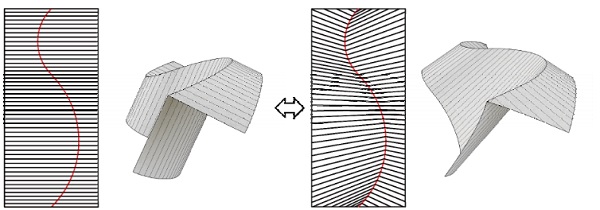
Fig. 7: The elastic transformation with the change in the rulings position (Bending only).

Our objective is to add more design freedom in such components so that we can explore variations of multi-functional, contextmatching, high-performance, efficient, and super cool-looking designs.

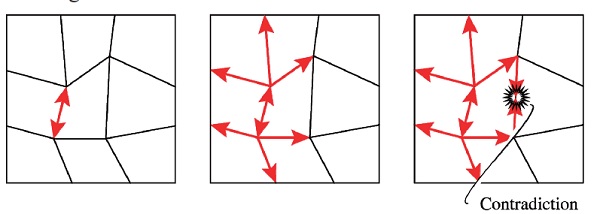
Fig. 8: Contradiction of fold angles in quadrangle mesh rigid origami.

In order to design such a kinetic structure in a relatively big scale, it is useful to use geometric method that requires no or few material deformation in order to achieve the overall transformation. Two major geometric approaches for achieving mechanical structures are 1) to use bars and rotational hinges to construct scissors mechanism, e.g., the works of Santiago Calatrava and Chuck Hoberman; and 2) to use plates and hinges to form polyhedral surface linkage with a synchronized motion, i.e. rigid origami.

Fig. 9: Implementing rigid origami with thick panels.

In this paper, we focus on the designs of the latter, since they have an advantage over the bars and hinges mechanisms in the sensethat they can form a kinetic watertight surface; a watertight surface is suitable for partitioning architectural spaces. However, unlike the bar linkage models, the form of rigid origami structures is heavily constrained, and it is has been very hard to find really useful design solutions.

Fig. 10: Stage 1: Design Abstraction; articulation experimentation of crumpled paper

There have been studies of rigid origami for forming kinetic surface such as Miura-ori, Ron Resch’s Pattern, and Chuck Hoberman’s designs. Especially, mechanisms based on a quadrilateral mesh such as Miura-ori produce 1DOF synchronized motions. This implies that the whole structure transforms by asserting force to a part of the structure.

Fig 11: Stage 1. Common Library (Shape Typology Toolkit)

Recent studies generalize theses structures to achieve further design freedom. Tachi proposes computational design methods to obtain variations of miura-ori-like quadrilateral mesh structures while preserving their flat-foldability and rigid-foldability. However, since this method uses continuous transformation from one pattern to another, the achievable forms are restricted by the initial patterns, the finding of which is still an important yet unsolved problem.

Fig 12: Stage 2. Group Brief: Dynamic Solar Shading (members: Emilie Hergott, Nicolas, Leduc, Sophie Pennetier, and Simon Schleicher); upward motion actuated by downward force on exterior edge.

In order to find the form variations of 1DOF rigid origami, we propose a modeling method that combines physical curved folding and computational design method. We have performed a workshop [6] based on this approach. The results demonstrated that the method is feasible and useful. This also suggests a new paradigm of design methodology.

Fig 13: Stage 2. Group Brief: Dynamic Solar Shading; hexagonal array of articulated shading elements

Curved folding is a piece of paper folded along curved creases; it is formed by combining folding and bending of the paper. In a geometric sense, a curved folded shape is a developable surface comprising the patches of smooth (G2 continuous) developable surface: plane, generalized cylinder, tangent surface, and generalized cone.

Fig. 14:Stage 2. Group Brief: Doors and Openings (members: Jacek Jaskólski, Thorsten Lang, Ana Maria Marcu, Ioanna Symeonidou, and Liam Woolley); animation in Rigid Origami Simulator. Notice the triangulation added to enable a mechanism.

Fig. 15: Stage 2. Group Brief: Doors and Openings; two layer rigid plate model sandwiching a paper hinge, pattern generated using Grasshopper definition by Tomohiro Tachi.

Even though each of these smooth patches only makes relatively simple form, the existence of creases make the surface freely configurable, enabling globally non-developable complex surface, e.g., approximated hyperbolic surface and elliptic surfaces, the sculptures by David Huffman, the early computer graphics works of Ron Resch, and product designs by Gregory Epps.