Compact reconfigurable kirigami

Gary P. T. Choi¹, Levi H. Dudte², and L. Mahadevan^2,3

¹Department of Mathematics, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA

²School of Engineering and Applied Sciences, Harvard University, Cambridge, Massachusetts 02138, USA

³Departments of Physics, and Organismic and Evolutionary Biology, Harvard University, Cambridge, Massachusetts 02138, USA

Kirigami involves cutting a flat, thin sheet that allows it to morph from a closed, compact configuration into an open deployed structure via coordinated rotations of the internal tiles.

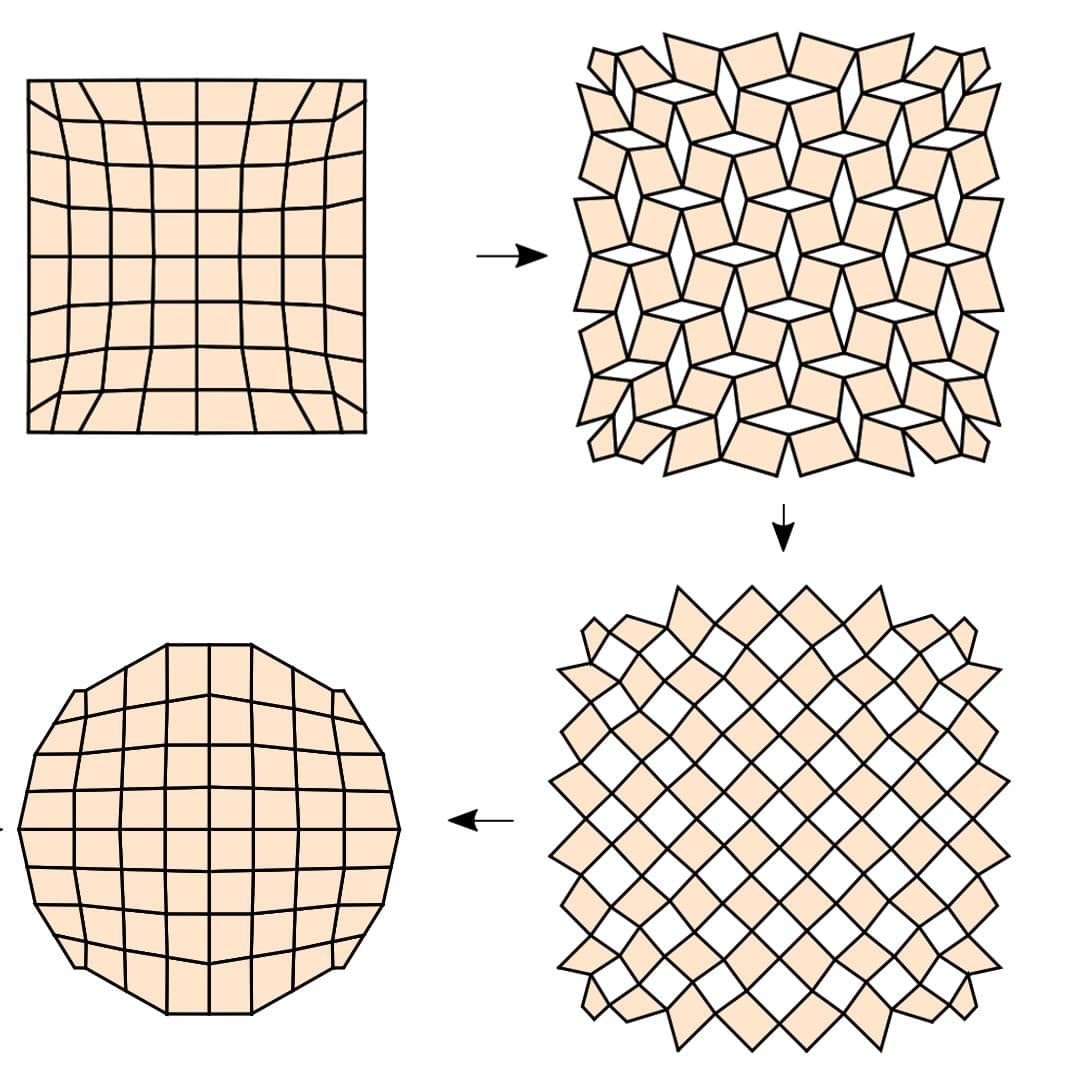
By recognizing and generalizing the geometric constraints that enable this art form, we propose a design framework for compact reconfigurable kirigami patterns, which can morph from a closed and compact configuration into a deployed state conforming to any prescribed target shape, and subsequently be contracted into a different closed and compact configuration.

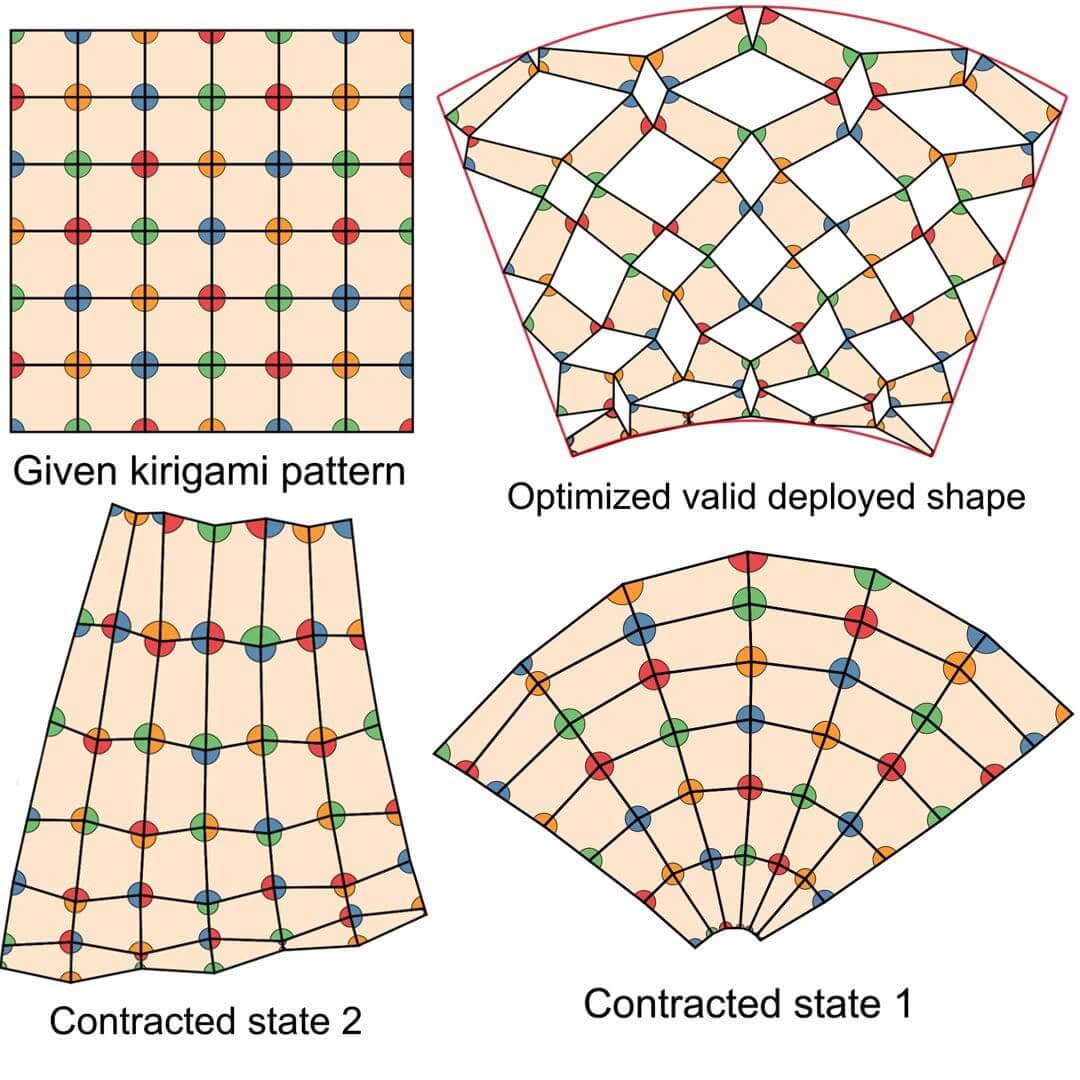We further establish a condition for producing kirigami patterns and mechanisms which are reconfigurable and rigid deployable allowing us to connect the compact states via a zero-energy family of deployed states. All together, our inverse design framework lays out a path for the creation of shape-morphing material structures.

Kirigami is the art of using cuts in a single sheet of paper that allow for changes in the shape of the sheet via coordinated rotations of the connected facets.

In recent years, the art form has motivated the design of metamaterials wherein architected cuts on a flat, thin sheet of material can lead to unusual properties not found in most naturally occurring materials, such as a negative Poisson’s ratio.

There have been a vast number of studies on the geometry, topology, and mechanics of kirigami with applications to the design of nanocomposites, shape-morphing sheets, inflatable structures, soft robots, etc.

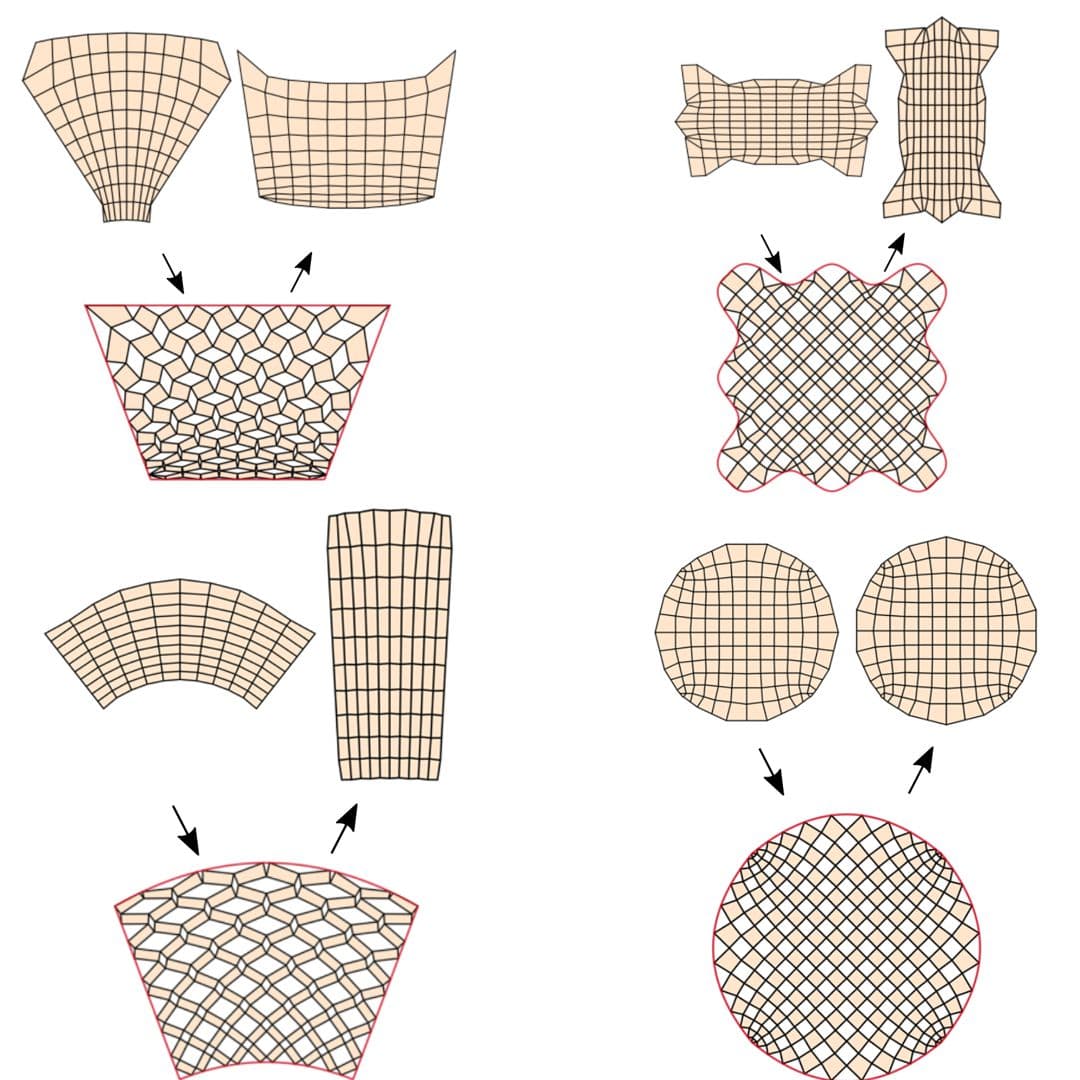Almost without exception, the deployed kirigami structures are open and periodic, and the property of admitting multiple closed and compact contracted states has been addressed only in a few well-known periodic regular kirigami patterns, and lead to states that are related to each other via global rotations.

Since kirigami derives its properties via coordinated rotations of the individual cells, it is natural that the problem of kirigami design is close to the design of mechanisms, in which a set of moving parts are connected by kinematic joints to form a deployable structure.

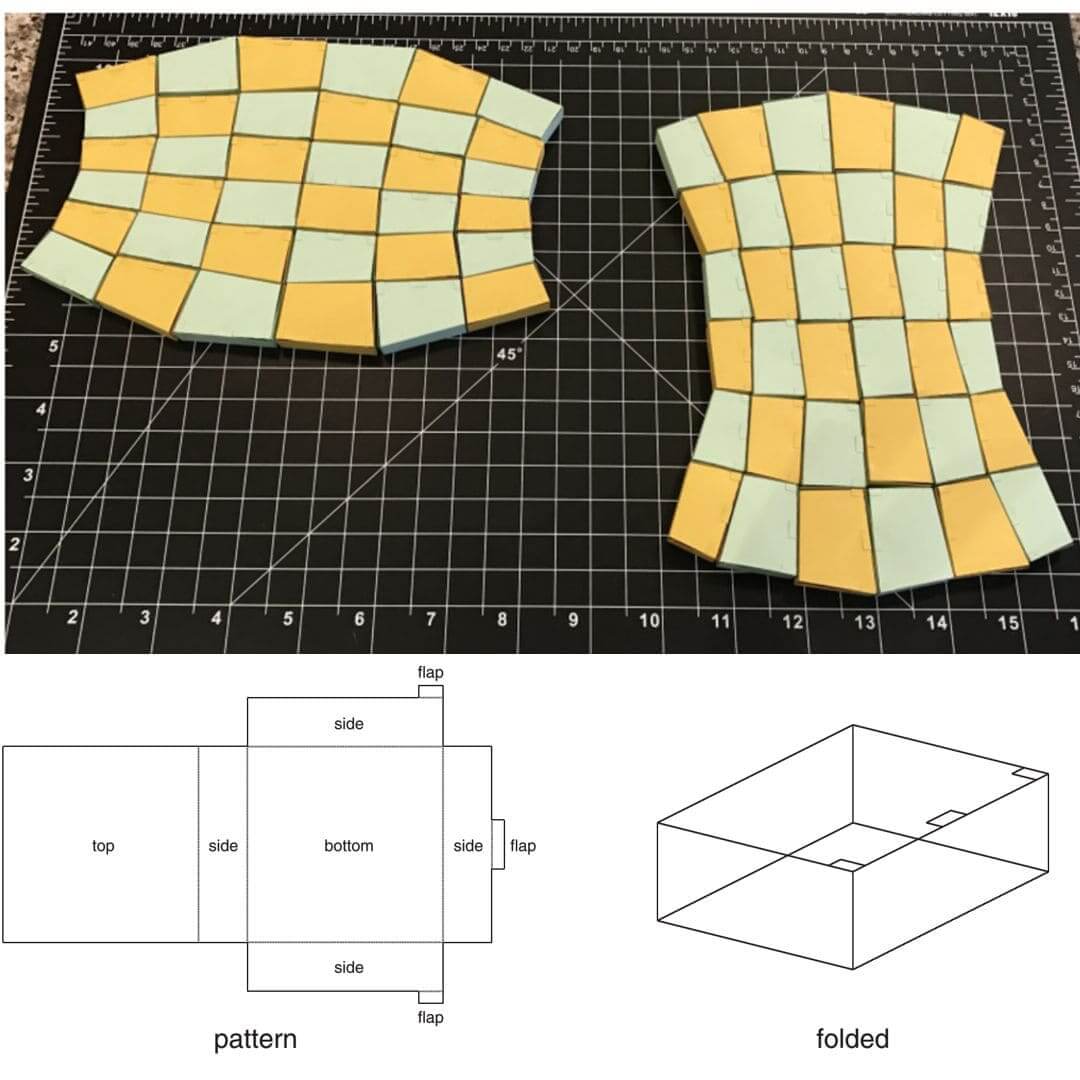
However, we note that while kinematic mechanism designs mainly focus on rigid-deployable structures formed by rigid bars, our inverse kirigami framework is applicable to both rigid and stretchable materials.

Furthermore, by focusing on how the angles and edge lengths of the tiles in a given kirigami pattern can be changed to achieve the desired properties, we circumvent the role of designing structural topology for mechanism design.