Kerf Bending

Kerf bending: ruled double curved surfaces Manufacturing

Mara Capone, Emanuela Lanzara

¹Emanuela Lanzara

Knowledge of geometric properties of surfaces is crucial for the resolution of many manufacturing problems. Developability is an important intrinsic property of a surface, because it allows its manufacture starting from a flat “strip” of a “flexible” and “non-deformable” material.

Digital fabrication technologies are evolving and becoming more and more widespread. Knowledge of fabrication methods available and parametric design tools, based on geometry, are changing the designer way to think.

Advances in this field promotes the experimental use of new materials but also the innovative use of traditional materials, such as wood. Our research, in the field of wooden curved surfaces fabrication, move from developable surface manufacturing and from “paneling” to “kerfing”.

This technique consists in transforming a rigid material in a flexible one and the problem to solve is how to cut the flat shape to obtain the design surface. This is a quite simple question to solve for a developable surface but it is a very complex problems to address for double curvature surface manufacturing.

Geometric genesis of surfaces and knowledge of their properties are crucial for solving many problems, both constructive and measurement. A developable surface can be manufactured starting from a flat “strip”, using a flexible and non-deformable material.

This is a very important feature of the surface. Geometry studies the properties that don’t change and, therefore, the shape of the “strip” to obtain a certain configuration, after a series of rigid movements.

Differential classification of surfaces, introduced by Leonhard Euler and subsequently used by Monge, allows us to group surfaces according to the definition of curvature, which will be precisely defined by Carl Friedrich Gauss in 1902, in four categories: surfaces with zero curvature, surfaces with positive curvature, surfaces with negative curvature and surfaces with variable curvature.

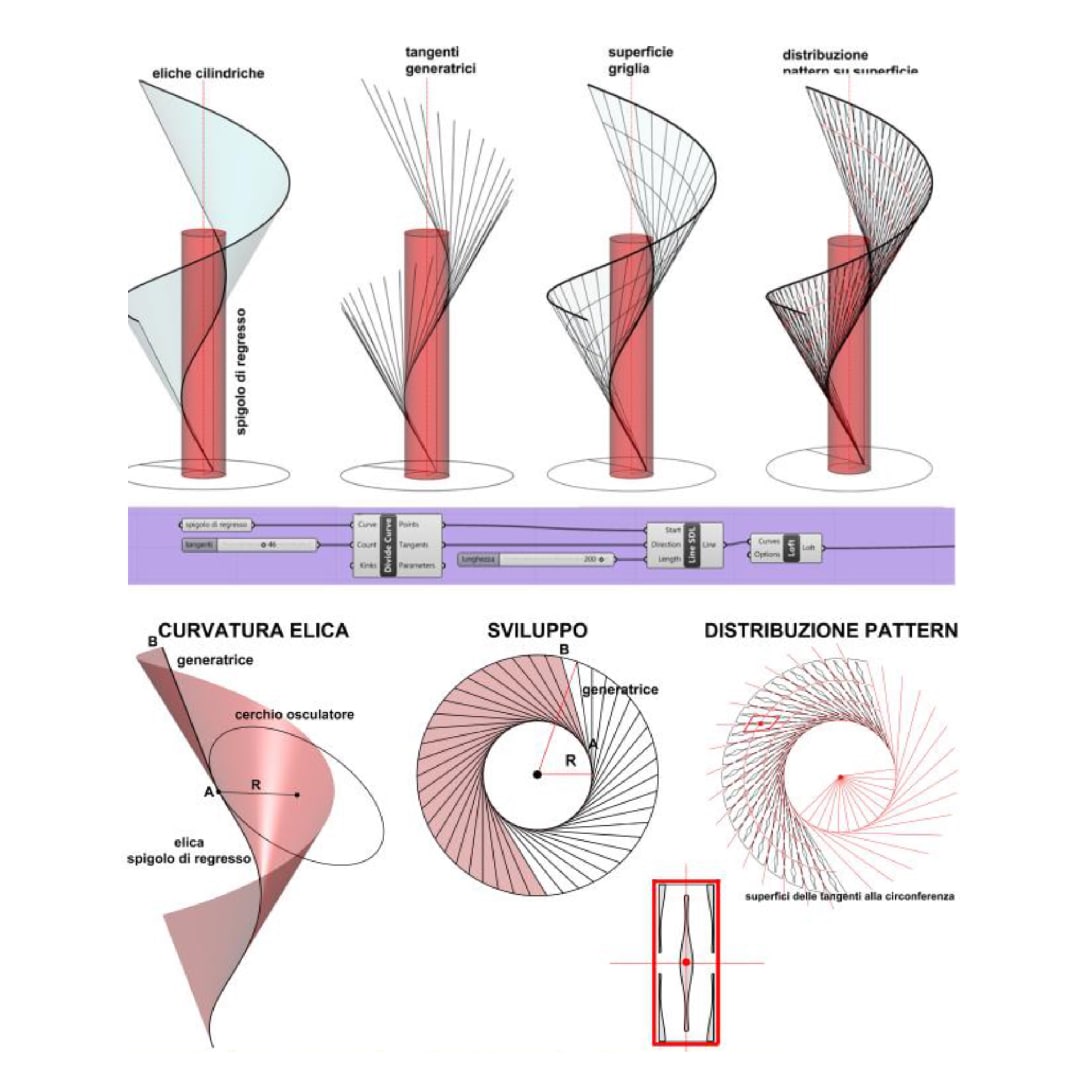
A developable surface is a surface for which every generatrix intersects the generatrix infinitely close, then: – when they intersect on curve c (edge of regression), we have tangent developable; – when they intersect in a point V (the edge of regression is a point), we have a conic surface; – when they intersect at infinity, we have a cylindrical surface.

The case of the developable helicoid is the simplest, in fact, if the edge of regression is a cylindrical helix, in order to generate the surface we can construct the tangent at a point P and then make it move along the helix.

There are two different approaches to define approximate develop of non-developable surface: first we can design the surface and then we can find the flat shape to manufacture it, or we can design 3D surface morphing a planar surface.

We can divide and approximate the 3D surface in order to cover a complex shape by developable strips, which can be unfolded to the plane in an isometric way, without stretching or tearing. In this way we can fabricate 3D complex shape using materials that can be bent in one direction or rigid material with no possibility of being bent at all.

In our research we have considered materials and manufacturing techniques that can solve approximation problems allowing non isometric transformation of the panel thanks to “cuts”, kerfing, or “overlapping”, bending.

The kerfing technique consists in subtracting material in some points of the panel in order to improve its flexibility. The maximum radius of curvature, that the panel can reach, depends on the material, the panel thickness, the type of kerf and the different distribution ways on the panel in relation to the curvature of the design surface.