In this Grasshopper example file, you can create a lattice pattern on a dress by using the Axolotl plugin.
In this Grasshopper example file written by Seghier Khaled, you can model a parametric Doyle spiral.
In this grasshopper example file, you can generate a series of fractal polygons on the faces of a Platonic solid.
In this Grasshopper example file, you can use the Physarealm plugin combined with the Dendro Plugin to simulate a growing fractal-based facade.
In this Grasshopper example file you can use the Physarealm plugin to simulate a parametric chair with a 3D organic shape.
In this Grasshopper example file you can use the Physarealm plugin to simulate the growth of a voxelized structure under a roof.
In this Grasshopper example file you can use the Rabbit plugin to generate L-system based columns.
In this Grasshopper example file you can use the Rabbit plugin in order to create a tree like fractal structure and then use the Kangaroo2 plugin to generate a tensile-like mesh as a shade.
In this grasshopper example file You can use the Mesh+ plugin combined with Weaverbird to model a parametric fractal mesh.
In this Grasshopper example file You can use the tOpos plugin to optimize a central Column for supporting the floor slabs.
In this Grasshopper example file You can use the Physarealm plugin to create a growing fractal-based pattern on a base surface.
In this Grasshopper example file you can use the Kangaroo2 plugin to model a differential growth pattern on a base surface .
In this Grasshopper example file You can use the Rabbit plugin to create a parametric table based on an L-system fractal.
In this Grasshopper example file you can use the Kangaroo2 and Peacock plugin to generate a parametric diffusion pattern on a ring .
In this grasshopper example file you can use the Physarealm plugin to simlulate a series of growing particles on a surface .
In this grasshopper example file you can use the Kangaroo2 Plugin to simulate a differential growth pattern on a surface.
In this grasshopper example file you can use the "Lorenz Attractor" component from the Chimpanzee`s plugin as a base for modeling a Polyline attractor.
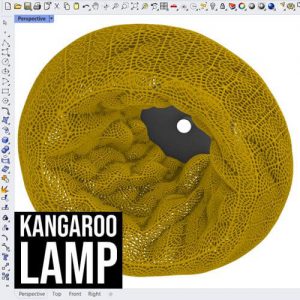
In this Grasshopper example file you can use the kangaroo colliders component to deform a mesh as a parametric Lamp.
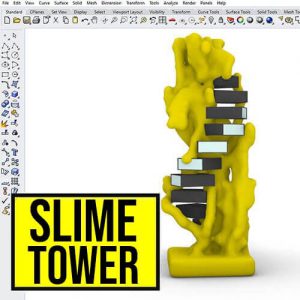
In this Grasshopper example file you can use Physarealm plugin which simulates a slime mold's growth to generate different tower forms and shapes.
In this Rhino Grasshopper Definition you can use the Kangaroo Plugin to deform a building's facade by a differential growth pattern. You can also use the wind force for further deformation.
In this grasshopper example file you can use a combination of Force field components and the Stella3D plugin to create a parametric cloth.
In this grasshopper example file you can generate a fractal-like sturcture between a series of points and a Nurbs surface.
In this grasshopper example file, you can genterate a 2D aggregation of polygons and create different parametric forms.
In this grasshopper example file you can model a spiral and then use the L-systems patterns (Rabbit Plugin) to create a branching structure.
In this grasshopper example file you can model a simple parametric fractal branching model using the anemone plugin.
In this grasshopper example file you can model a parametric L-system based earing by using the Rabbit plugin.
In this grasshopper example file you can use the Dendro and Weaverbird plugin to model a parametric frame ring.
In this grasshopper example file, you can simulate agents, flocking inside a mesh which is generated based on a fractal curve.
In this grasshopper example file, you can model a curve branching fractal using the anemone plugin.
In this grasshopper example file you can generate different L-system fractals on a sphere using the Rabbit plugin.
In this grasshopper example file you can model a smooth fractal mesh using the Mesh+ plugin combined with weaverbird.
In this grasshopper example file you can create a fractal system similar to the growth of a tree.
In this grasshopper definition you can create a space filling fractal by generating grid of rectangles and applying a growth system to it.
In this grasshopper definition by making a loop with the anemone plugin, you can model a surrounded recursive cube.
In this grasshopper definition by creating a loop with the Anemone plugin and defining an attractor which moves around a base circle you can create a series of spheres that grow smaller recursively.
In this grasshopper definition by creating circles around a base circle and using the "Trim With Region" component you can create a recursive flower-like pattern in grasshopper.
In this grasshopper definition, you can create a series of 2d voronoi cells based on thhe julia set fractal.
In this grasshopper definition, you can model a series of triangular extrusions by defining a simple polygon. Anemone plugin has been used for the recursive loop.
In this grasshopper definition, you can create a loop that scales a base curve recursively. You can also add rotation or other transformations at the end of the loop. Finally, you can loft between the curves.
This grasshopper definition can help you model fractal trees fast.This Python fractal tree example file can also be used as an exercise for how to write fractals in python and use boolean to make your code more advanced.
In this grasshopper definition, you can create a voxelized shell shape by subtracting two volumes and finally model a Triply Periodic Minimal Surface.
In this definition you can model a parametric fractal based on circles.In each step the circles scale down and cover a portion of the circle's circumference.
In this definition you can model a fractal based on a square which builds two smaller squares on one of its edges.
In this definition you can make a fractal rotating polygon by using the Anemone plugin. First we are going to explode the curve to its segments and then evaluate a point on the edges. This recursive algorithm will produce the final rotating polygons.
In this Grasshopper definition you can use the Anemone Plugin to rotate a tower around itself. First we will define the rotation and scaling factor and then we will extrude the base square to model the tower.
In this Grasshopper Definition by using the Anemone plugin you can model a recursive pattern that connects each corner of the face to the center. You can also Mesh+ & Weaverbird to prepare a mesh or a Nurbs surface for the division process.
In this definition we have used the Anemone plugin to model the Apolloian fractal. In mathematics, an Apollonian gasket or Apollonian net is a fractal generated starting from a triple of circles, each tangent to the other two, and successively filling in more circles, each tangent to another three.
This grasshopper definition is generated by putting simple scaling and rotating into a loop through Anemone Plugin, however it is quite different from the method that mathematician generate the Hilbert Curve fractal. A Hilbert curve is a continuous fractal space-filling curve.
In this example you can model a 3d sierpinski fractal by using the recrusive behaviour of the Anemone plugin and then you can use the weaverbird plugin to smooth the results.
In this grasshopper definition you can learn how aggregation method works by creating a loop with the Anemone plugin. In each iteration, the faces of the meshes will generate a new face.
In this grasshopper definition we have used the Rabbit Plugin to produce a parametric L-System by defining rules and number of agents (Turtles). The Starting position has been found on a sphere
In this definition you can use the shortest walk plugin to produce a venation pattern between a series of random points.
In this grasshopper definition you can aggregate a custom module (Tile) by defining junctions using Fox Plugin.
By using the Subdivide Triangle component of Lunchbox Pluging you can model a simple Sierpinski Triangle in Grasshopper3d. Basically, this component Subdivides a triangle into self-similar cells. First, you have to give a closed triangular curve or surface to subdivide then by defining four different Booleans you can control the divisions. The first one controls the center triangle and the rest control the 3 adjacent triangle areas.