Automatic Triangular Grid
Automatic triangular grid generation on a free-form surface using
a particle self-organizing system
Fengcheng Liu, Ruoqiang Feng
The Key Laboratory of Concrete and Prestressed Concrete Structures of Ministry of Education, Southeast University, Nanjing 211189, China


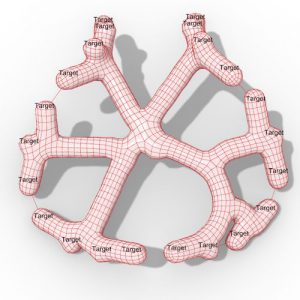
Fig. 1 Free-form structures
A novel method for automatic triangular grid generation on a free-form surface based on Coulomb’s law is proposed in this paper, which we refer to as the particle self-organizing system (PSOS).
The self-organizing of particles is realized by the interaction between charged particles, which brings about an even layout of particles. After connecting the optimized particles, a uniform triangular grid is generated.
First, a moderate number of grid points are randomly arranged on the surface. Second, the grid points are regarded as charged particles with the same charge in the electric field and free to move driven by the Coulomb force.
Third, the equilibrium state of the particle system is acquired according to the equivalent electric field intensity of each particle. Finally, the triangular grid is generated by the Delaunay method.
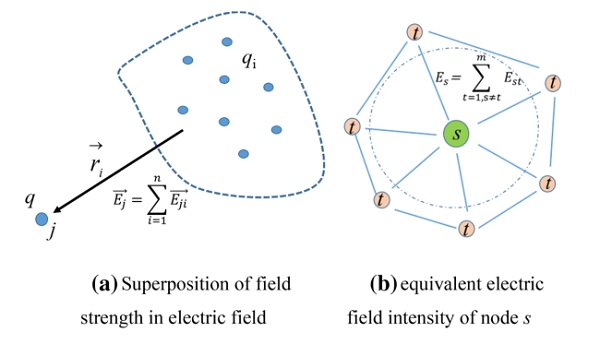
Fig. 5 Calculation of equivalent electric field intensity
According to the different motion space of particles, the particle self-organizing system can be divided into an indirect method and a direct method.
The particle motion space of the indirect method is the parameter domain; the grid layout is obtained first and then mapped back to the space surface.
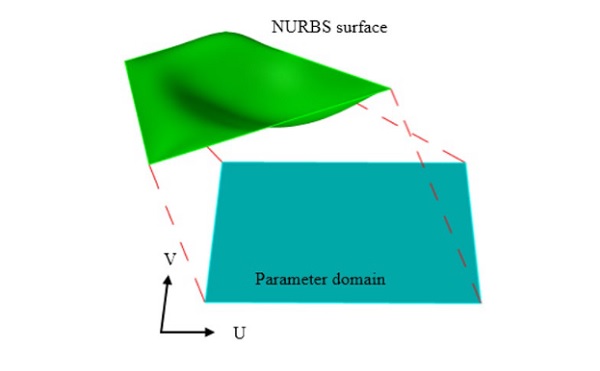
Fig. 9 Mapping from parametric domain to space surface
The particle motion space of the direct method is the physical space of the surface; a grid is generated directly on the physical domain, and no mapping process is needed.
The case studies indicate that both methods can generate a uniform triangular grid quickly, with the direct method having a higher grid quality.

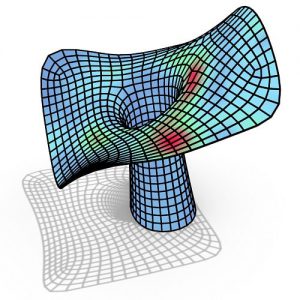
Fig. 10 An arbitrary surface
In the twenty-first century, as free-form design has gained popularity, several free-form grid structures have appeared throughout many cities, becoming landmarks of the region with their splendid visual effects.
Compared to a conventional surface, a free-form surface is unable to be expressed accurately by means of one or several analytic functions, and the curvature of such a surface is a complex shape, as shown in Fig. 1.
Therefore, with the rapid rise of free-form grid structures, an urgent problem has come along with it, namely, how to mesh these changeable freeform structures to show their esthetic implications without losing the architectural vision of smoothly shaped building envelopes.

Fig. 11 The initial particles
Topology optimization is one of the effective methods used to create an efficient structural grid on an imposed surface.
Peter and Gilbert, Paul et al., and Gao et al. have made substantial progress in this area. However, as Peter pointed out that a grid generated via topology optimization cannot be applied to the actual projects directly and further refinement is needed.
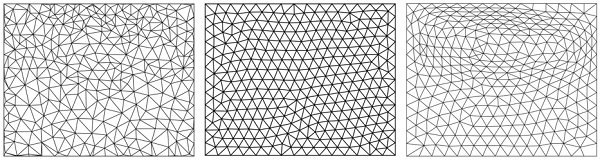
Fig. 12 Grid layout on parameter domain
To obtain a better grid with the excellent mechanical properties over a free-form surface, Winslow et al. presented a new algorithm that considers the mechanical performance based on a traditional genetic algorithm.
Su et al. also conducted a similar study in this area, proposing an improved wave-front method, which used the structural stress trajectory as the guideline and pushed the grid forward in the direction of the guideline.
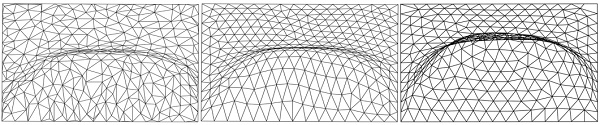
Fig. 13 Grid layout on physical domain
This can avoid blindness and disorder in the advancement process. However, the disadvantage of this method is that the uniformity of the grid is poor, and some distorted unit cells appear.
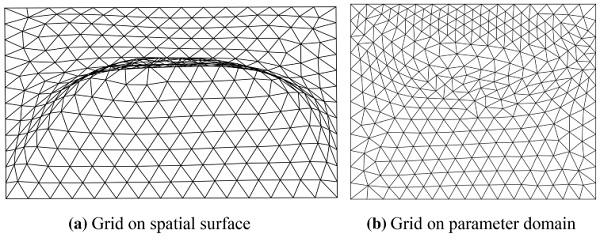
Fig. 14 Grid generation considered the effect of attraction
Sometimes, one must admit that architects are most concerned about whether the grid has the advantages of fluency and uniformity, and the structural mechanical properties seem to be less important.
Some research has reported the progress of grid generation over a free-form surface without taking their structural performance into account.
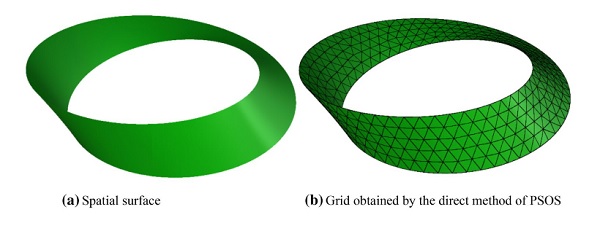
Fig. 15 Mobius band
Ding proposed a new method for a free-form surface grid generation, referred to as the iso-parametric line dividing method, which is based on a non-uniform rational B-spline (NRUBS) curve.
Li proposed a re-interpolation reflection meshing method to avoid the uneven grids caused by the distortion curvature. Moreover, the extension of the grid meshing modes and the optimization of the grid system were also discussed.
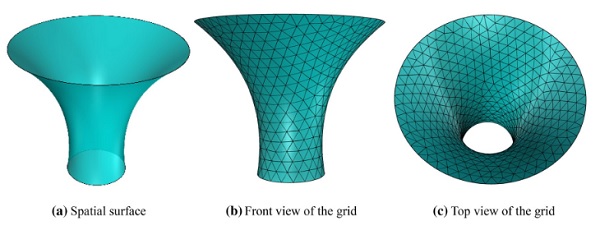
Fig. 16 The EXPO sun valleys in Shanghai
Wei and Gao concentrated on the mesh generation based on surface flattening and mapping theory. Persson and Strang developed an iterative technique for the actual mesh generation based on a physical analogy between a simplex mesh and a truss structure.
Shimada and Gossard et al. invented an interesting grid generation method called bubble mesh generation. In its actual implementation, the bubble method generated node configurations that yielded virtually no ill-shaped triangles or tetrahedrals.
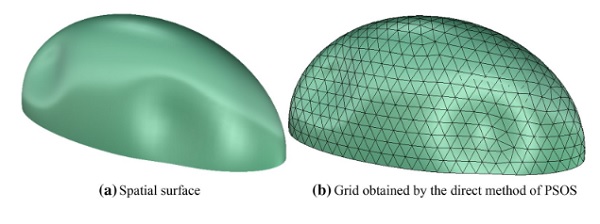
Fig. 17 Admirant entrance building
Similar to the bubble method, Zheleznyakova regarded the grid nodes as interacting particles and developed a new approach for the triangular grid generation based on the molecular dynamics method.
However, the drawback of this method is that the grids generated by it are not smooth enough to be directly applied to actual projects.
























Comments