Branching Fractal

Fractals are intricate patterns or structures that are self-repetitive at every scale, meaning they appear the same or similar regardless of the level of magnification.

Emerging from simple mathematical equations, fractals defy our classical sense of scale and provide a visual representation of infinity.

Their unpredictable and beautiful nature has captivated scientists, mathematicians, and artists alike.

Fractals can be found in nature, such as in the branching of trees, the structure of snowflakes, and the formation of coastlines, while others are products of pure mathematics.

Delving into the world of fractals allows one to appreciate the balance between chaos and order that exists both around and within us.

1- Koch Snowflake Fractal:

The Koch Snowflake is one of the earliest described fractals, named after Helge von Koch. Starting with an equilateral triangle, each side is modified by adding a smaller triangle at its middle, removing its base, and this process is repeated infinitely. With each iteration, the perimeter of the shape increases, pushing the boundaries of our understanding of length, as the snowflake’s perimeter heads towards infinity while its area remains finite.

2- Sierpinski Triangle:

The Sierpinski Triangle is a mesmerizing pattern of endlessly nested triangles. To visualize its formation, start with an equilateral triangle and remove a smaller triangle from its center. This process is repeated for the remaining triangles, and so on, indefinitely. The resulting fractal showcases a balance between positive and negative space, revealing a pattern that is both intricate and endlessly repeating.

3- Hilbert Curve:

The Hilbert Curve, named after mathematician David Hilbert, is a space-filling curve, meaning it tries to occupy as much of a two-dimensional space as possible without crossing itself. Beginning as a simple U-shaped curve, each iteration involves refining the shape, making it twist and turn more complexly. While it seems to fill up more space with each step, the curve never actually becomes a solid shape, no matter how many times it is iterated.

4- Quadratic Fractal:

Quadratic fractals arise from iterating quadratic functions in the complex plane. One of the most famous examples is the Mandelbrot set. When points from the complex plane are plugged into a simple equation repeatedly, their behavior determines whether they belong to the Mandelbrot set or not. The boundary of this set is where the magic happens: it’s an infinitely intricate fractal that reveals more details no matter how much you zoom in, showcasing the deep complexity that can emerge from simple mathematical rules.

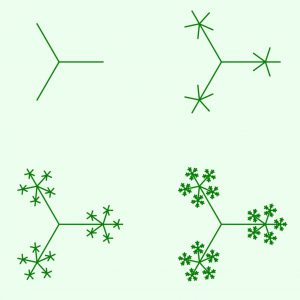
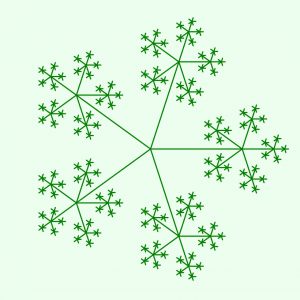
5- Branching Fractal:

Branching fractals are reminiscent of patterns found in nature, like the veins of a leaf or the branching of trees and rivers. Starting with a main ‘trunk’ or line, smaller branches sprout out at certain angles, and from these branches, even smaller branches emerge, and so on. The self-similarity is evident as each smaller branch mimics the pattern of the larger one, creating a visual representation of the recursive processes often found in the natural world.

Video References:

1 _ https://youtu.be/WFtTdf3I6Ug?si=SfGTI6kMQVE3HXwm

2 _ https://youtu.be/40p_YC0yZZQ?si=CdizReVypHUfb-XL

3 _ https://youtu.be/ackDGIKx1cw?si=Wr3Ys2Za5r1Cxixt

4 _ http://datagenetics.com/blog/march22013/index.html

5 _ https://youtu.be/-0ooIpJyCNc?si=yhm74ZR4LdISRM5B

Compilation Video by Zahra Ebrahimi , Mohammad Yazdi