String Art Generator
March 5, 2025
String Art Generator by Yiran is a grasshopper plugin which generates a string art sequence based on an input image. You can
Curve-Folding Polyhedra Skeletons through Smoothing
Suryansh Chandra, Shajay Bhooshan, Mustafa El-Sayed
Zaha Hadid Architects 10 Bowling Green Lane London, EC1R 0BQ UK
Figure 1: Curve-Folded Polyhedra Skeleton made of aluminium at the AA Visiting School Bangalore 2012
The research and prototypes documented in the paper operate in the context of the exciting potential of curved-crease folding in manufacturing curved surfaces from flat sheet material.
Figure 2: Student work in our workshop
This paper describes a designer-friendly computational method to design and fabricate a class of curve-folded geometries – our proposed method generates developable surfaces that are curved-foldable, skeletal representations of a given userdefined, convex mesh.
The work draws inspiration both from the precedent works of Richard Sweeney, Ron Resch etc. as also the observed ease of physical exploration, in paper, of such geometries by students in our workshops.
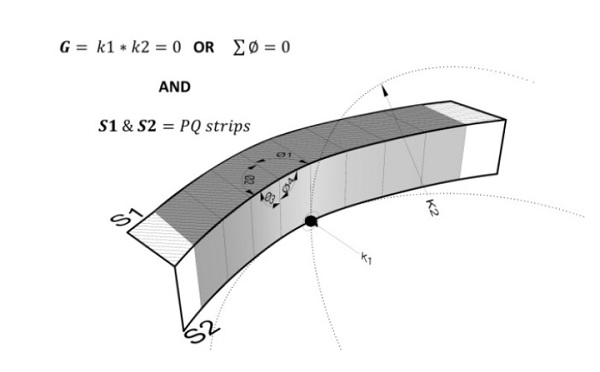
Figure 3: Essential requirements of a discrete representation
Further it also aims to address the current difficulties in recreating that ease in digital explorations. These difficulties stem both from the lack of appropriate geometric descriptions and constructive tools in ubiquitous CAD software; pointing towards the need for exploration-friendly digital methods to find and describe such geometries.
Thus, the key contributions of the paper stem from addressing these issues: An extensible, exploration-friendly digital method and the description of procedural methods to produce manufacturing data from digitally produced geometry. The paper concludes with potential avenues of architectural scale application of the method.
Figure 4: Designed surface in white, derived surface in dark gray
Most of the precedents projects and available literature on design methods highlight the difficulty in developing an intuitive, exploratory digital-design method to generate feasible 3D geometries.
Our initial survey of methods included both the iterative optimization-based method and the simple constructive method – the method of reflection. Most methods, including the two above, presented difficulties towards incorporation within an intuitive, real-time, edit-andobserve exploratory method.
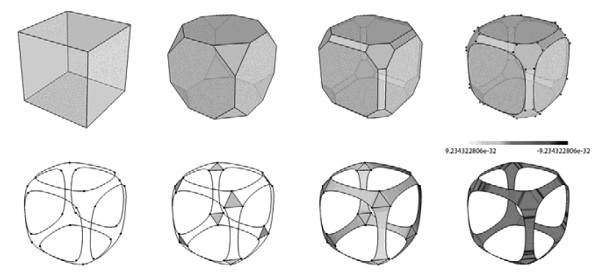
Figure 5: Geometric operations to extract designed surface from polyhedron
Further, most of the methods aim at applicability towards a wider range of feasible geometries whereas our interest was a specific class of geometries.
Lastly, they are also iterative methods that minimize one or more ‘energies’ with the aim to capture the physical behaviour of sheet-material. For an extensive overview on the precedents, and computational methods related to curved crease folding, we refer the reader to a survey.
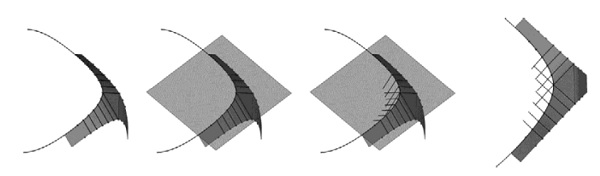
Figure 6: The method of reflection produces intersecting surfaces
Our key point of departure was to geometrically construct feasible geometry like Mitani and Igarashi as opposed to a physically-based iterative construct-and-correct solution.
As such, the method benefits speedy computation and thus an edit-and-observe exploratory strategy to design. Critically however, it is applicable to a specific class of geometries, i.e. convex polyhedra.
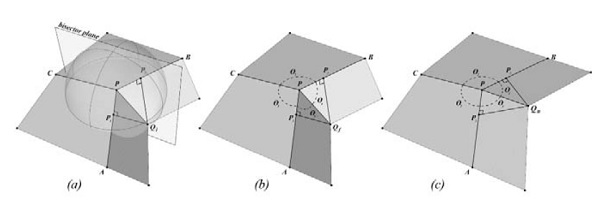
Figure 7: Calculating the derived surface
It is worth mentioning that we do implement an iterative solution to produce planarized polyhedra from non-planar meshes, to aid less restrictive modelling operations for the designer.
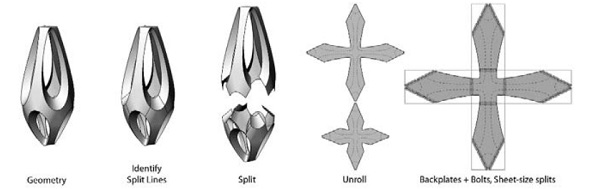
Figure 8: Process of CAD/CAM info generation
The paper described a method of generating a class of curve folded geometry – smoothed skeleton of convex polyhedra, as also producing the necessary fabrication information from the generated geometries.
Further, this paper also noted the intuitive nature of using polyhedral meshes and their manipulation using ubiquitous mesh modelling tools. This then enables speedy exploration of variations and the edit-and-observe strategies of designers.
Figure 9: Precise edge alignment in clusters of CFPs
Apart from the obvious benefit of using sheet material to produce curved surfaces, we also noted the fabrication benefits of such geometry in general.
They ease the on-site description of geometry and assembly of parts due to their capacity to be formed withminimal effort. In our workshops, we have been able to build 2 metre tall CFPs from sheet aluminium with teams of 10-15 students within a matter of 6-8 hours.
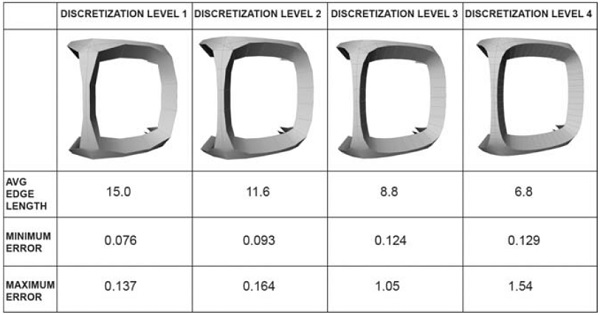
Table 1: Key results from unfold error measurements
Based on the prototypes and research thus far, we can envision the use of the method in the production of architectural scale assembly of skeletal geometries.
Figure 10: Parametric variations of the designed and derived surface computed from the same base polyhedron
Such folded geometries, especially from smooth sheet material such as aluminium or plastic, could also be beneficial in their use as false-work or lost form-work to cast concrete and other hardening structural materials.
