The Airshell Prototype
July 9, 2022
This paper by Alessandro Liuti, Sofia Colabella, and Alberto Pugnale, presents the construction of Airshell, a small timber gridshell prototype erected by employing a pneumatic formwork.
Fold Mapping: Parametric Design of Origami Surfaces with Periodic Tessellations
M. Gardiner1, R. Aigner2, R. Hanlon3, H. Ogawa
1Ars Electronica Futurelab
2Fachhochschule Oberösterreich
3Deakin University
We present a design method that prioritises in-context design for origami surfaces with periodic tessellations in a parametric CAD workflow using Grasshopper 3D.
The key design criteria are: target geometry surface, userdefined folding patterns as periodic tessellations, and fold resolution. Using an error minimisation solver, we generate developable crease patterns from nondevelopable meshes.
We evaluate our method through a study of a target geometry, Fold Mapped with various fold molecules at variable resolutions, and present a visual analysis as proof of form-fit to the target.
This method affords rapid development of origami surfaces, bypassing significant trial and error in by-hand design processes.
Software for origami design is a highly specialised topic and the utility of existing tools tends towards solving specific categories of design problems.
Examples of this intent can be as specific as Ronald Resch’s software to solve configurations of the triangular Resch pattern, towards more generalised tools like Origamizer by integrated into FreeForm Origami to find crease patterns for any given mesh, or Tachi’s earlier software Rigid Origami intended to explore and evaluate the rigidity of a given geometry or crease pattern, or an algorithm by intended to solve geometric surfaces with detailed analysis and composition of the Miuraori.
Overall, algorithms are specialised and design processes vary from engineers to artists, and from engineering requirements to aesthetic criteria.
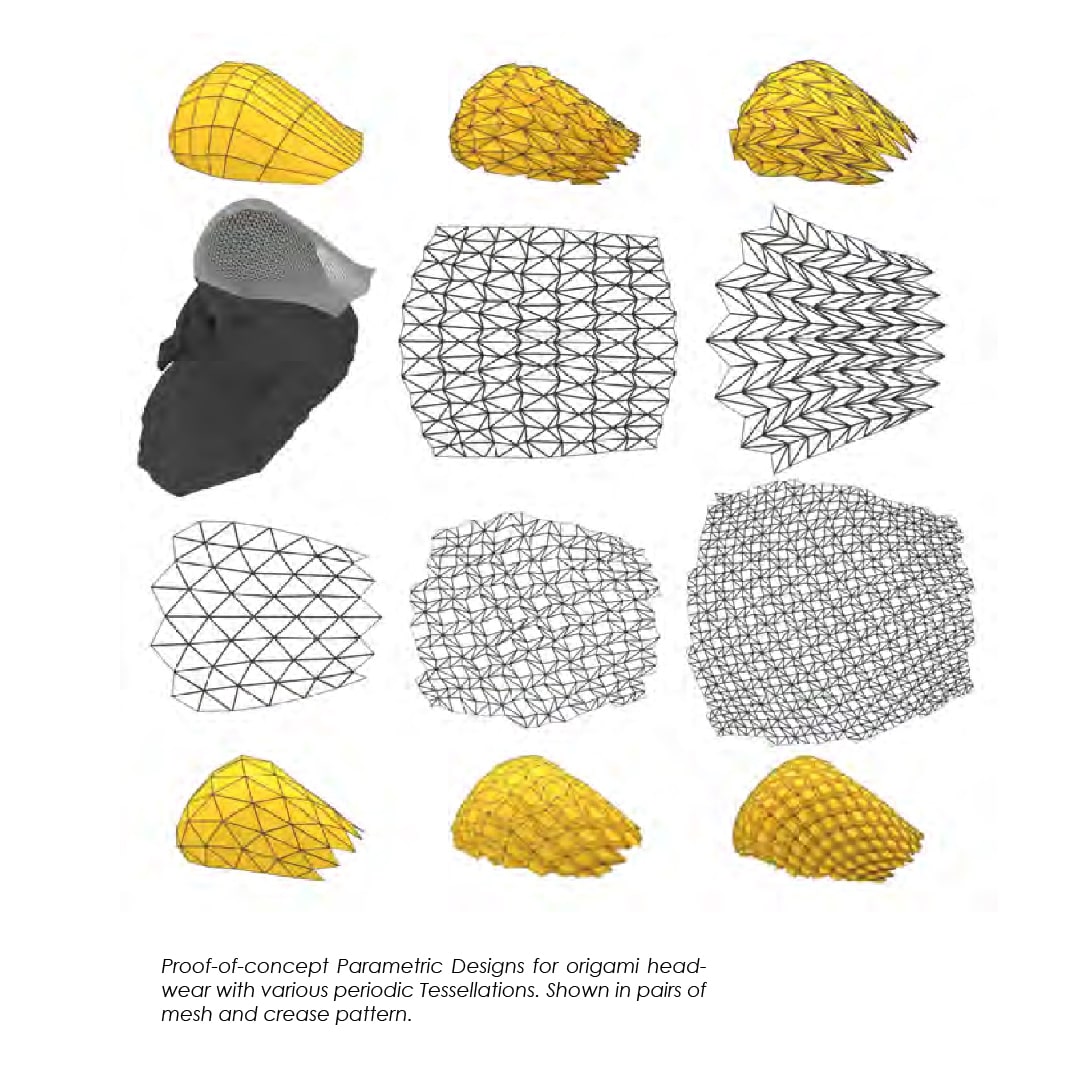In this paper, we focus on a design method to approximate geometric surfaces with periodic tessellations–also known as open corrugations–with the intent to explore off-grid and irregular configurations and to compare a range of patterns for a particular design target.
In addition to the aesthetic qualities of these patterns, we have a particular interest in open corrugations due to their deployability and application to kinetic origami systems such as Oribotics.
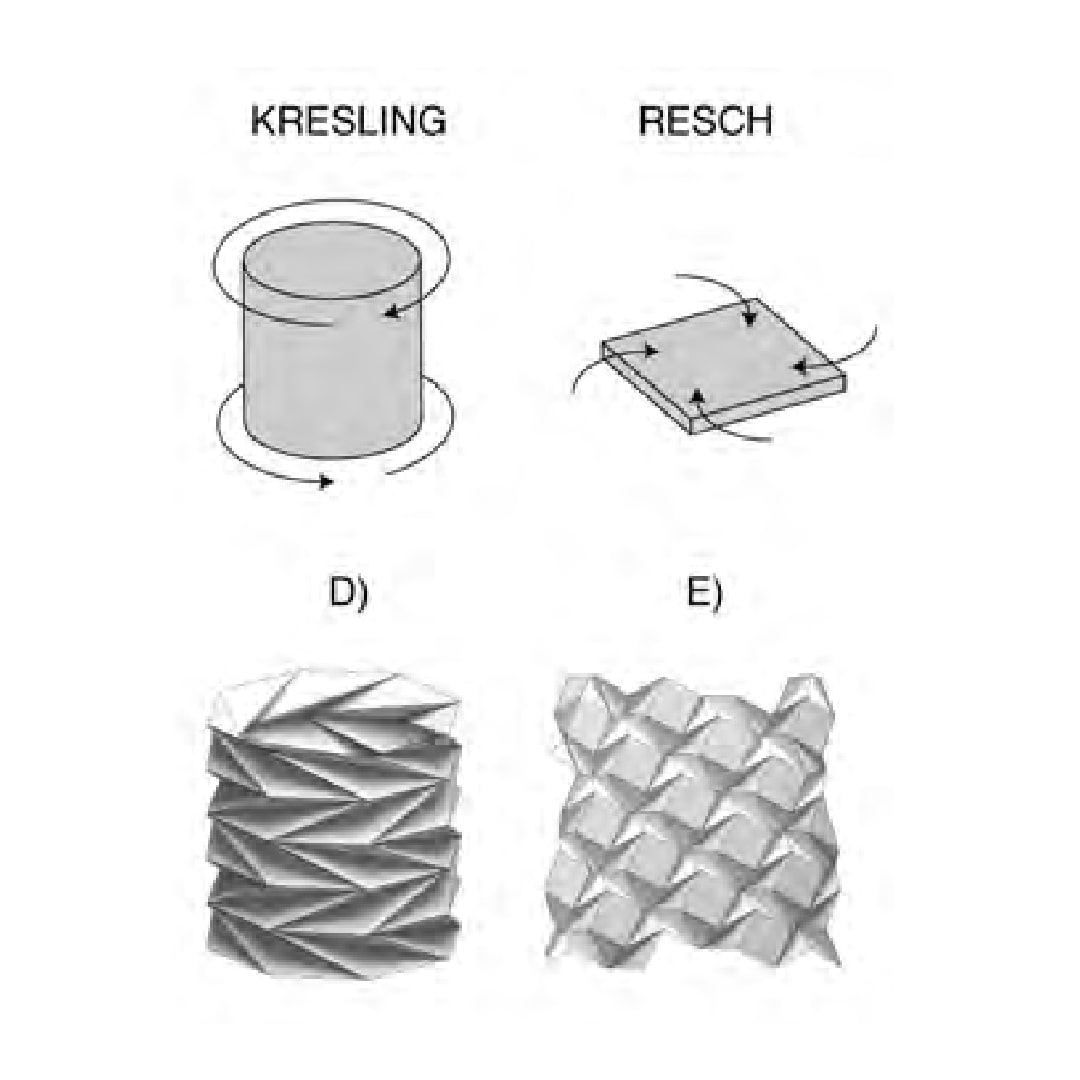
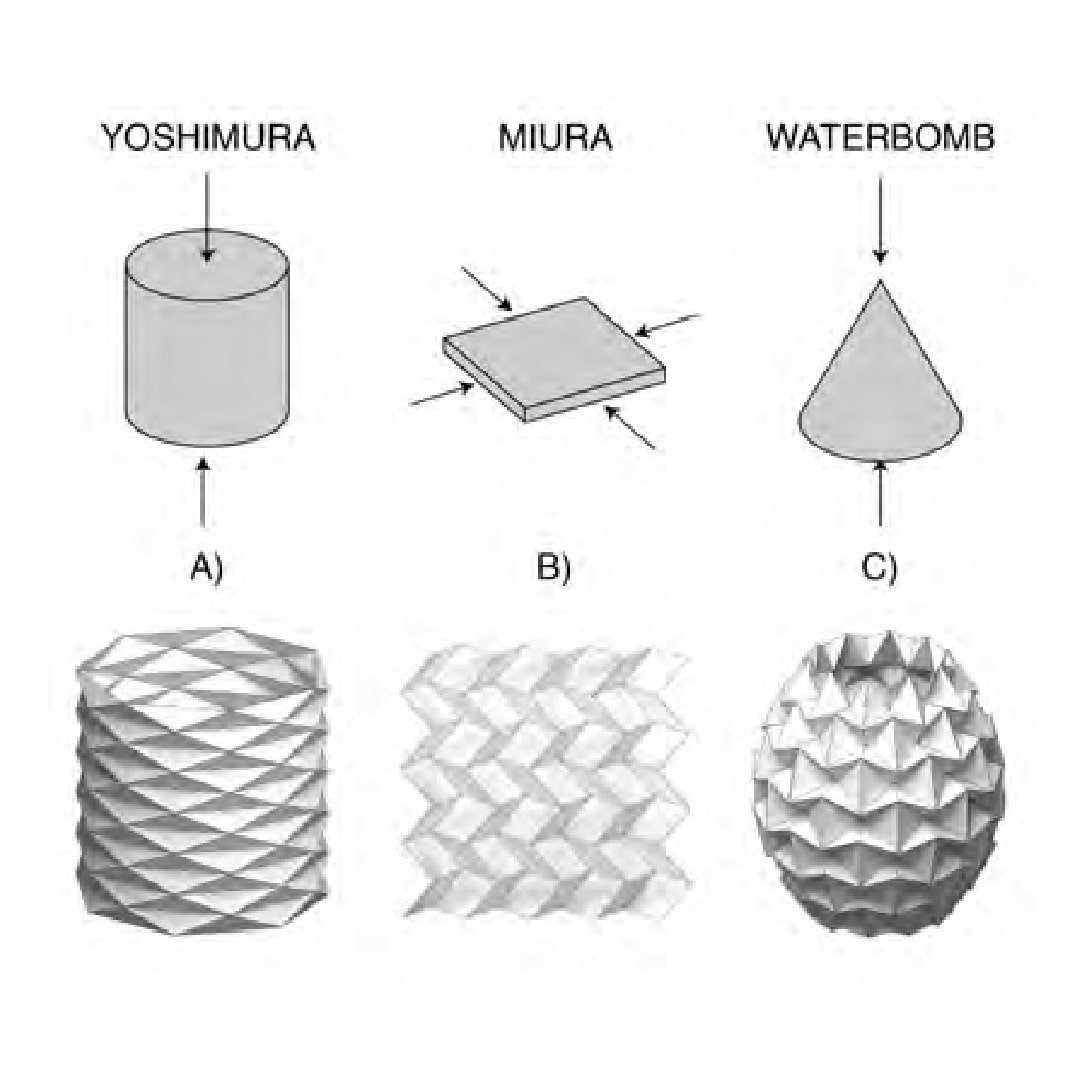In folded-plate structures, design criteria such as rigid-foldability, developability, target shape, and unit pattern have emerged in released software packages such as: Freeform Origami with Origamizer function a and point editing tools, oricreate as a command line interface, he Rigid Origami Toolbox for use in Matlab, and show a method for approximating curved surfaces with miura-ori, considering material properties to determine fold scale versus accuracy of the finished form.
The background for this research is the study of Natural Folding: how nature uses the language of folding, and we apply our findings in the domain of art and design.
We examined literature to decide which geometries to use in our work. We found that nature applies folding in many ways: to structurally code strings of proteins in DNA Origami, leaf unfurling patterns, insect wings, as a way to pattern the crushing power of folded laminations in the earth’s crust.
Based on these claims, we chose Rhinoceros 3D3 combined with the visual programming plug-in Grasshopper 3D4 as our design platform, especially as potential use cases are architecture and design.
In particular, Grasshopper 3D provides a popular design environment for parametric design in those disciplines, featuring an active community.
