Fractal Geometry Art
A fractal is an object or quantity that displays self-similarity, in a somewhat technical sense, on all scales.

[1]
The object need not exhibit exactly the same structure at all scales, but the same “type” of structures must appear on all scales.
 A plot of the quantity on a log-log graph versus scale then gives a straight line, whose slope is said to be the fractal dimension.
A plot of the quantity on a log-log graph versus scale then gives a straight line, whose slope is said to be the fractal dimension.
 The prototypical example for a fractal is the length of a coastline measured with different length rulers. The shorter the ruler, the longer the length measured, a paradox known as the coastline paradox.
The prototypical example for a fractal is the length of a coastline measured with different length rulers. The shorter the ruler, the longer the length measured, a paradox known as the coastline paradox.

[2]
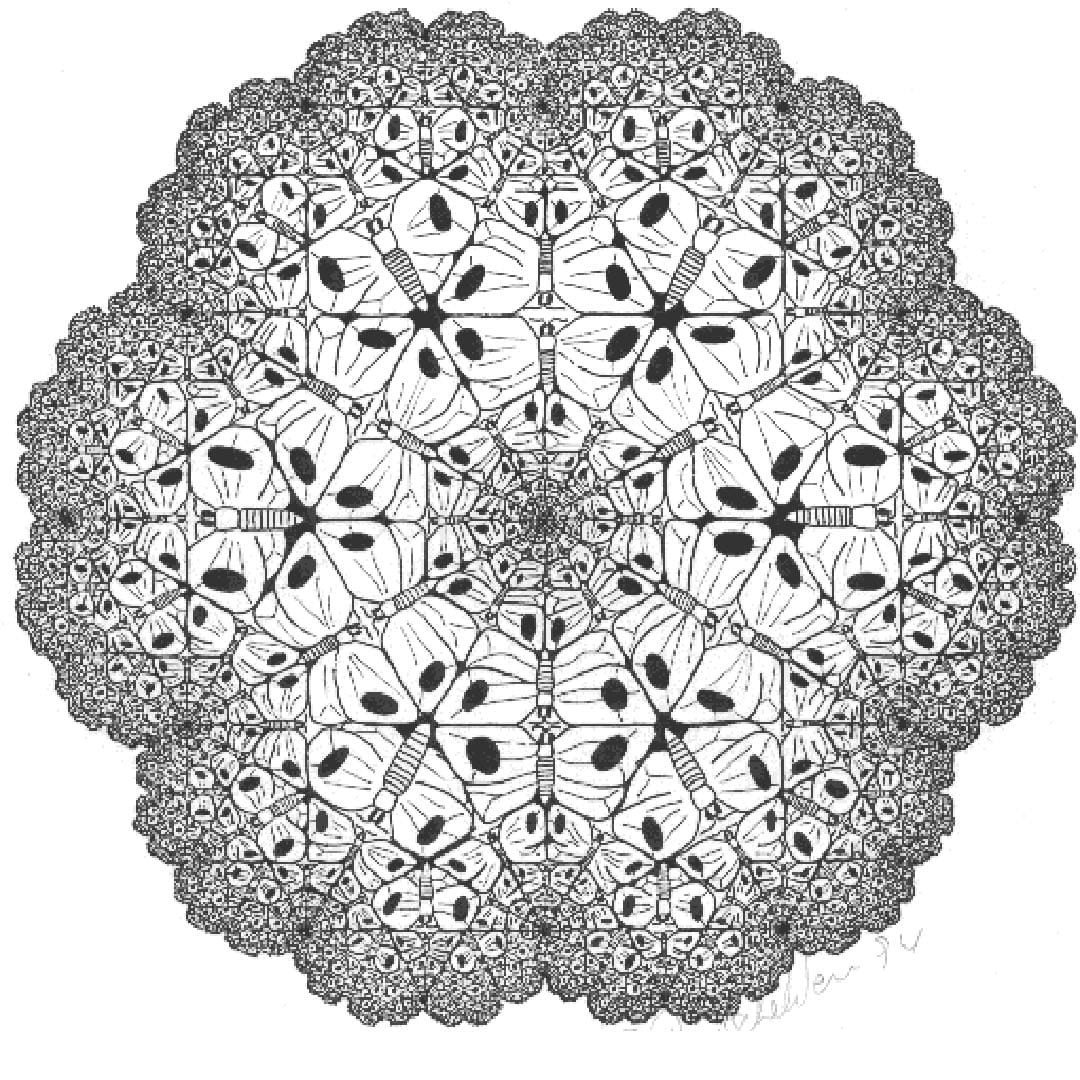
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension.
 Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set.
Many fractals appear similar at various scales, as illustrated in successive magnifications of the Mandelbrot set.

[3]
This exhibition of similar patterns at increasingly smaller scales is called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, the shape is called affine self-similar.

[4]
One way that fractals are different from finite geometric figures is how they scale. Doubling the edge lengths of a filled polygon multiplies its area by four, which is two (the ratio of the new to the old side length) raised to the power of two (the conventional dimension of the filled polygon).
[5]
Likewise, if the radius of a filled sphere is doubled, its volume scales by eight, which is two (the ratio of the new to the old radius) to the power of three (the conventional dimension of the filled sphere).

[6]
Fractals are not limited to geometric patterns, but can also describe processes in time. Fractal patterns with various degrees of self-similarity have been rendered or studied in visual, physical, and aural media and found in nature, technology, art, architecture and law.

[7]
Text Source: Fractal/wolfram.com
Fractal/wikipedia.org
Video Source:
1-CGI VFX Demo : “250,000,000 Particles Mandelbulb Render Using Arnold 4.0” by – Juanjo González / Youtube / The CGBros
2-Michael Hansmeyer: Building unimaginable shapes /Youtube / Michael Hansmeyer
3-Creating The Never-Ending Bloom / Youtube/ John Edmark’s
4-Math Beauty – Morphing Fractal Fruits (Ray Tracing)/Youtube/Alon Nahary
5-Unreal Engine 4 Mandelbulb 3d RealTime/Youtube/Art Hiteca
6-Hidden Structures of the Mandelbrot and Julia Sets/Youtube/Damnimp
7-4D Mandelbrot set rotation/Youtube/Bib993
8-FRACTAL ART-The Making of “DIRTY DENDRITES”-How to Tutorial/Youtube/Dirty Artist-Acrylic Pouring
9-Room Sculpture from the 3D Printer/Youtube/Voxeljet
10-coandco-new faces-Jérémie Brunet/Youtube/bib993
11-How to 3D Print a Fractal (Sierpinski Arrowhead Curve)/Youtube/Tom Rocks Maths



























Comments