Geometric Modeling

Geometric Modeling with Conical Meshes and Developable Surfaces

Yang Liu¹, Helmut Pottmann², Johannes Wallner², Yong-Liang Yang³, Wenping Wang¹

¹Univ. of Hong Kong

²TU Wien

³Tsinghua Univ., Beijing

In architectural freeform design, the relation between shape and fabrication poses new challenges and requires more sophistication from the underlying geometry.

The new concept of conical meshes satisfies central requirements for this application: They are quadrilateral meshes with planar faces, and therefore particularly suitable for the design of freeform glass structures.

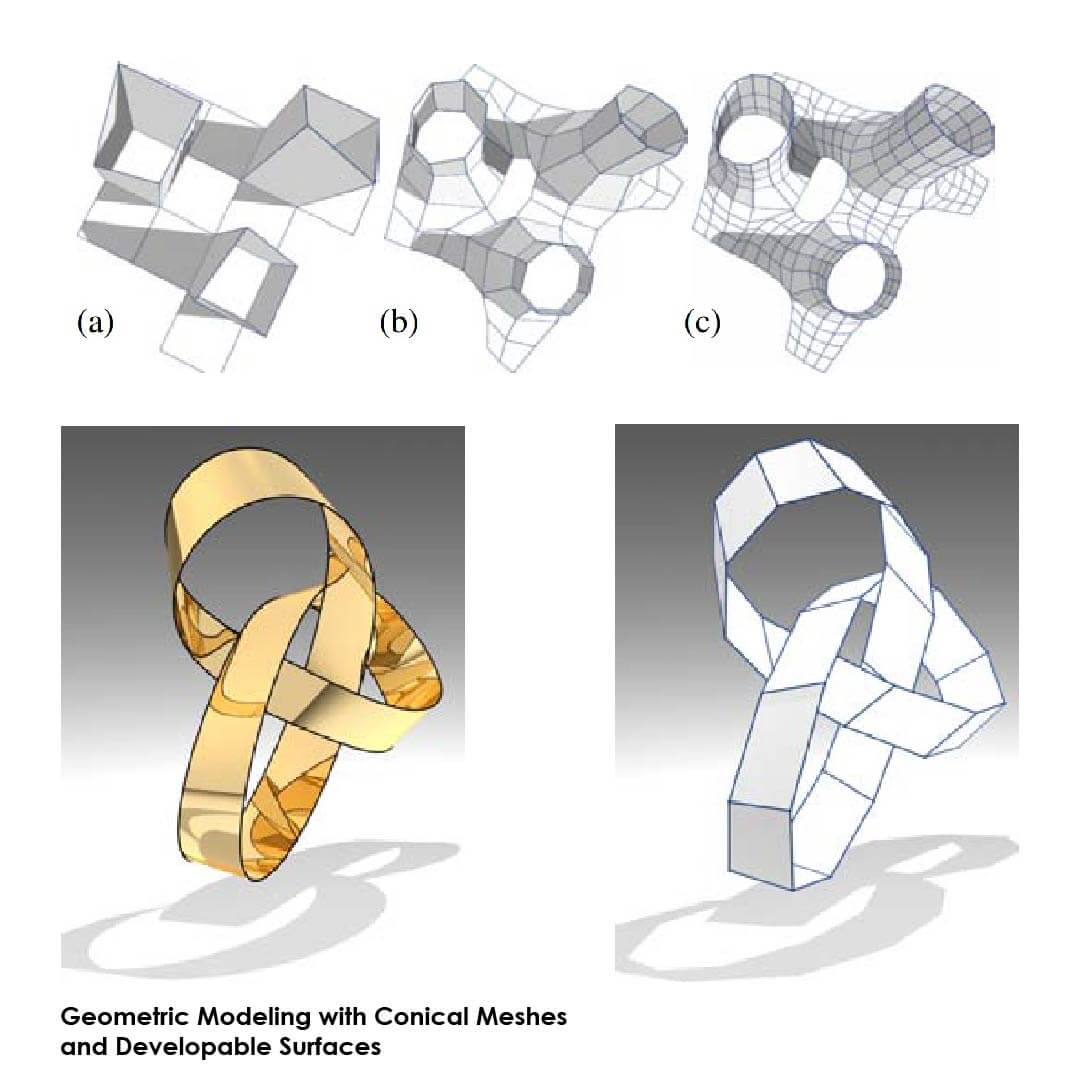Moreover, they possess a natural offsetting operation and provide a support structure orthogonal to the mesh. Being a discrete analogue of the network of principal curvature lines, they represent fundamental shape characteristics.

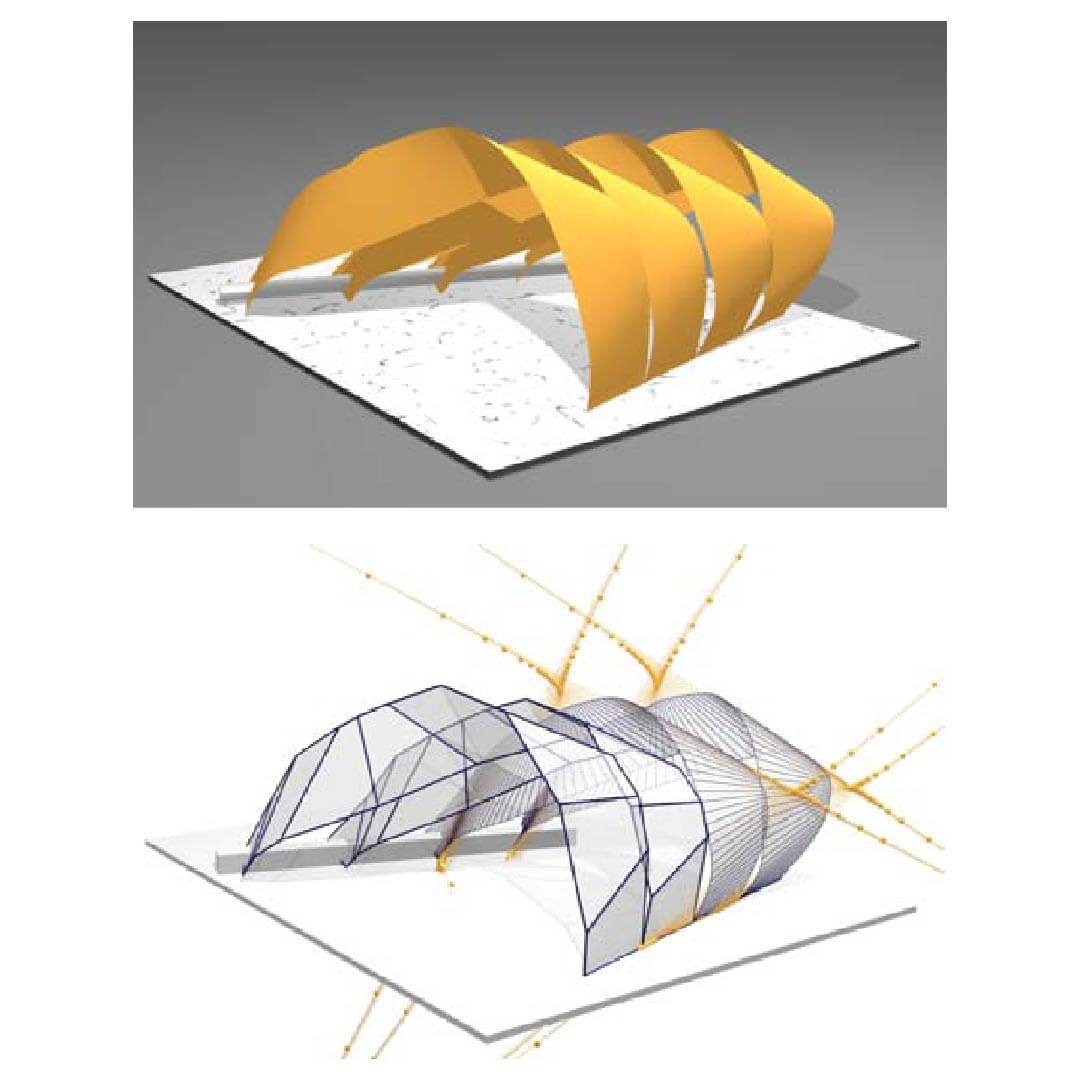We show how to optimize a quad mesh such that its faces become planar, or the mesh becomes even conical. Combining this perturbation with subdivision yields a powerful new modeling tool for all types of quad meshes with planar faces, making subdivision attractive for architecture design and providing an elegant way of modeling developable surfaces.

The original motivation for this research comes from architecture, where freeform shapes are becoming increasingly popular, but the actual construction poses new demands on the underlying geometry.

Gehry Partners and Schlaich Bergermann and Partners [Glymph et al. 2002] argue why freeform glass structures with planar quadrilateral facets are preferable over structures built from triangular facets or non-planar quads.

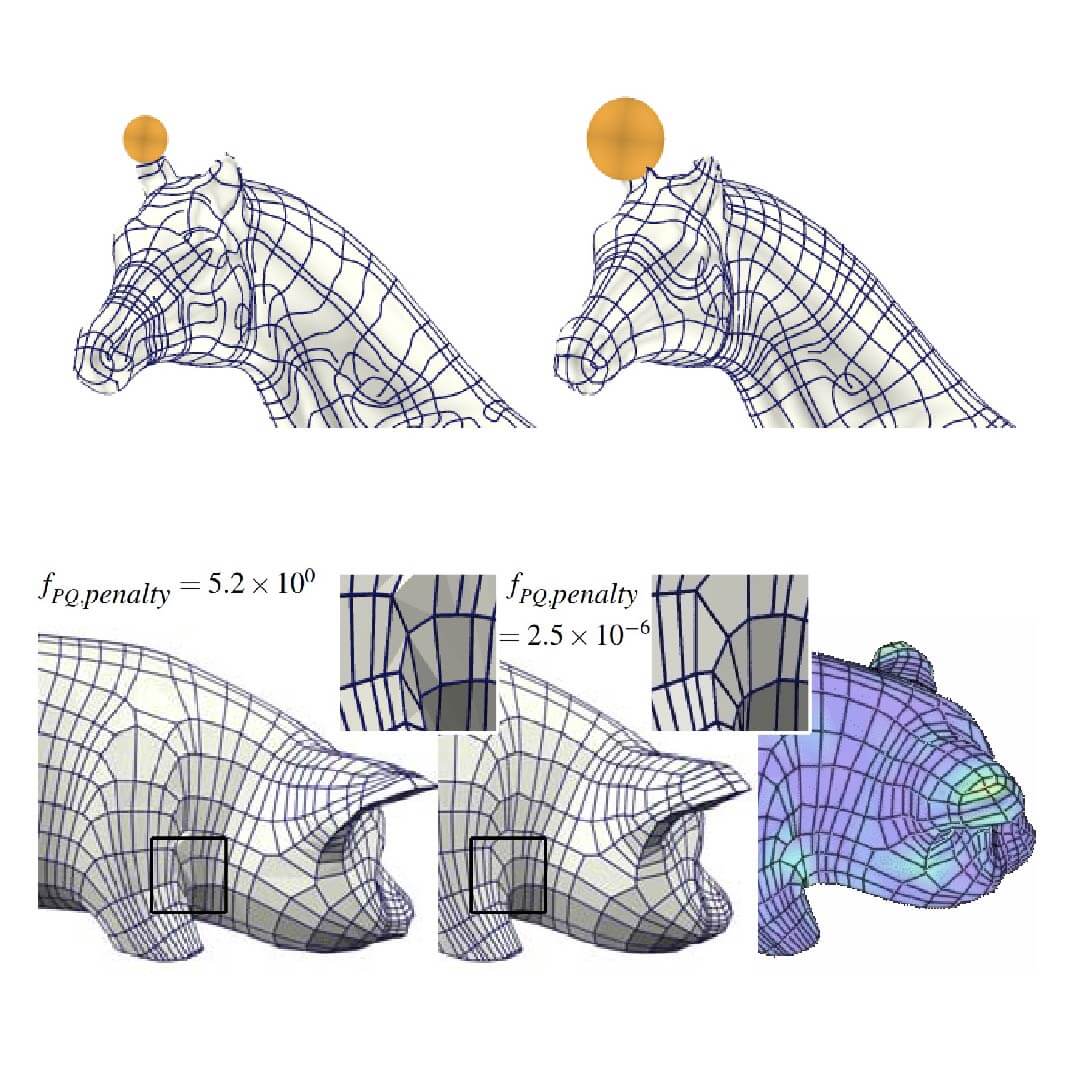The authors also show a few simple ways to construct quad meshes with planar faces. However, despite the huge amount of work on mesh processing and the interest in discrete differential geometry [Desbrun et al. 2005], we are not aware of a thorough investigation of this topic from the perspective of geometry processing.

The study of quad meshes with planar faces – called PQ meshes henceforth – will lead us to interesting geometric results, in particular to conical meshes, a discrete counterpart of principal curvature lines which have not been considered before.

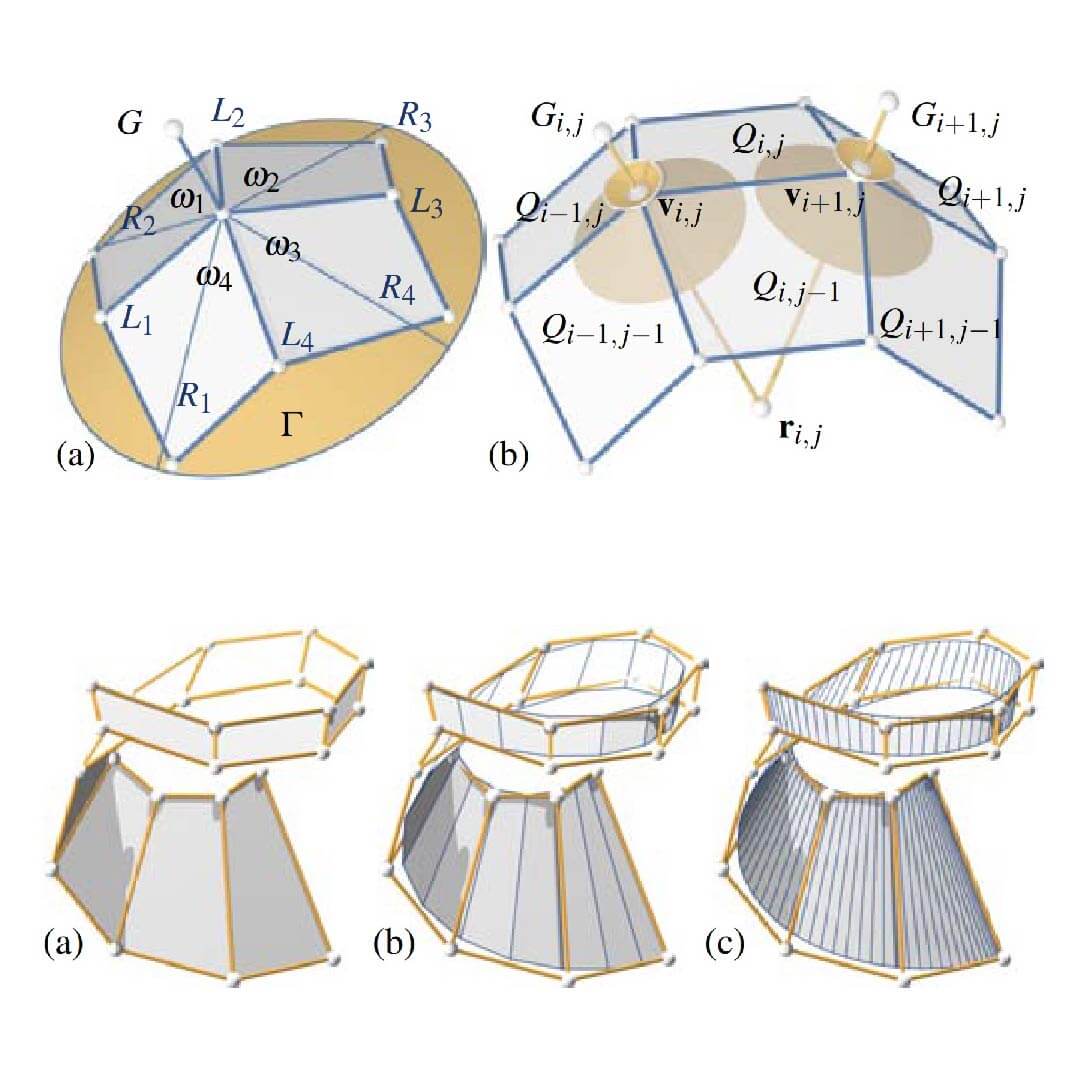Algorithms which perturb a quad mesh into a PQ mesh can nicely be combined with subdivision. This makes subdivision a promising tool for architectural design and also provides a new and elegant approach to modeling and approximation with developable surfaces.

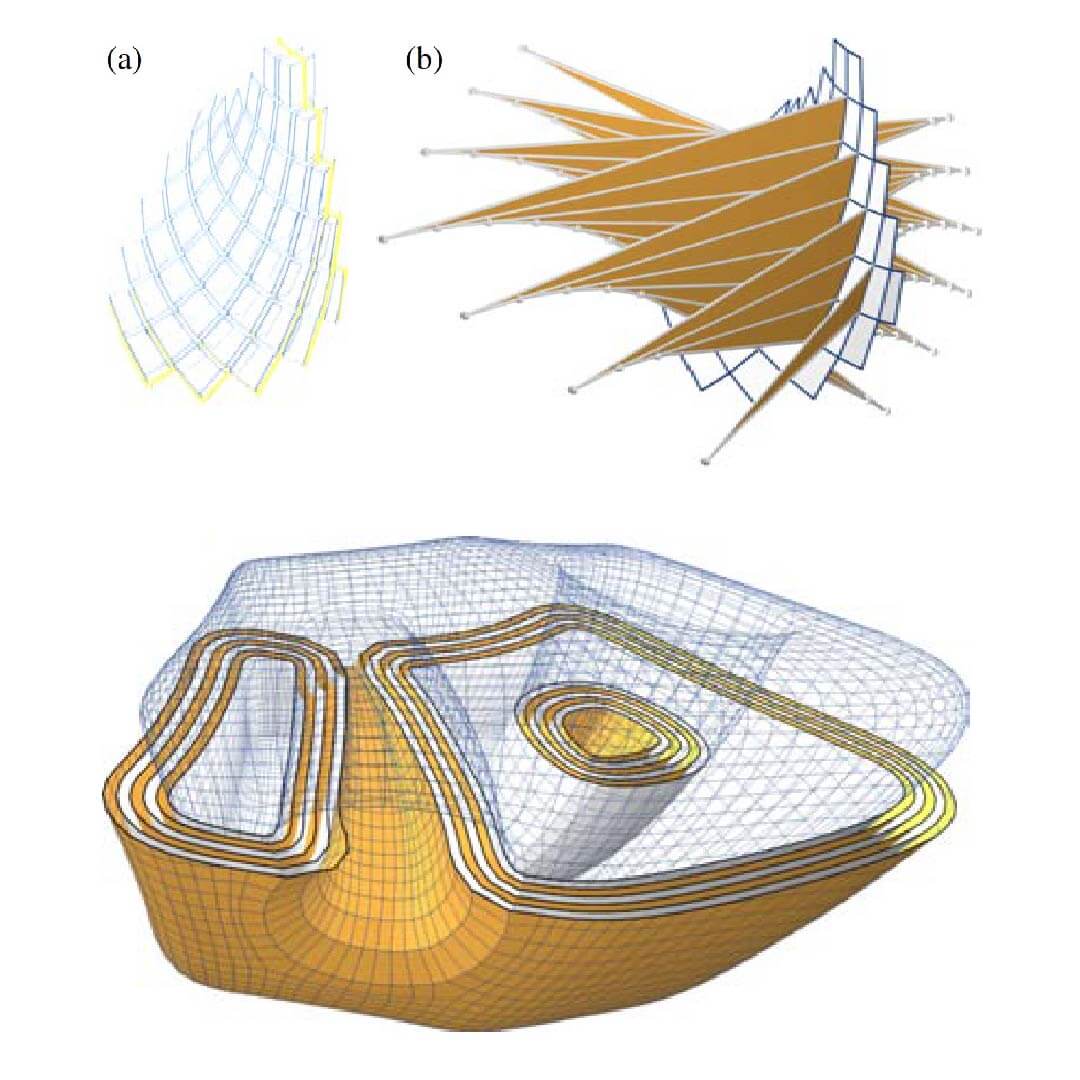
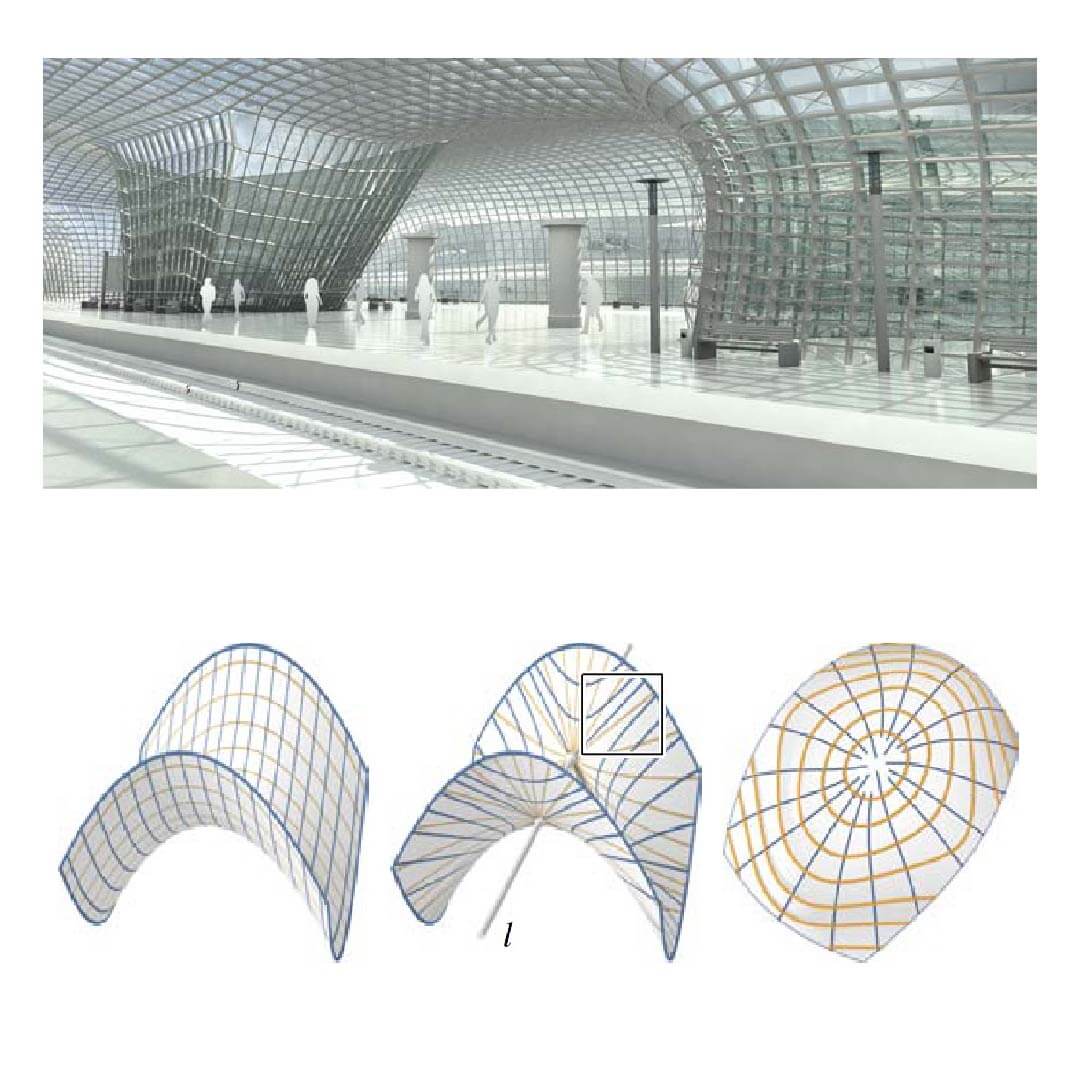Our experiments show that the proposed subdivision approach to developable surface modeling is a powerful new tool.

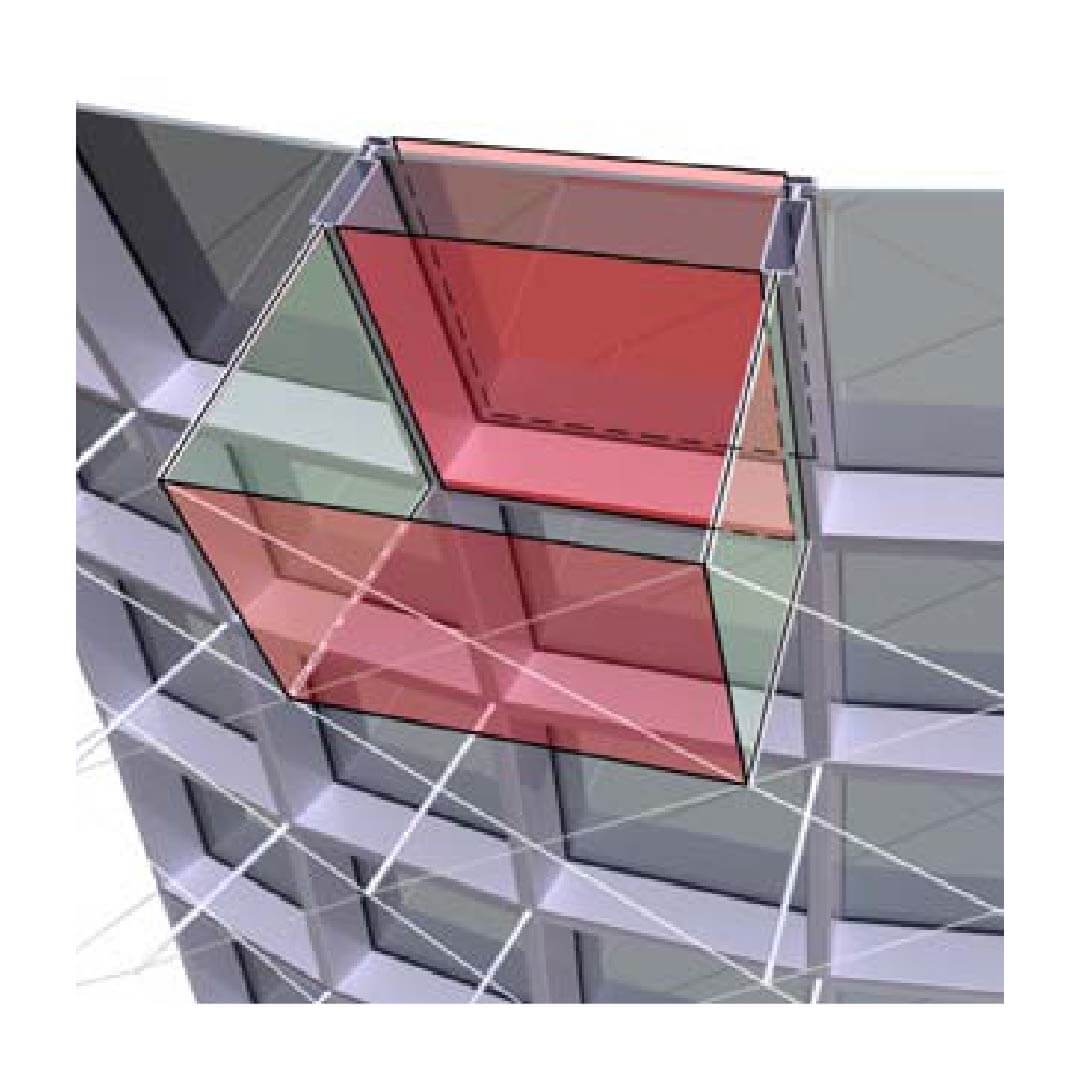The elimination of the singular curve from the actually designed patch is simplified by the multiscale approach inherent to subdivision: Planarization results in convex quads and thus eliminates singularities from the designed patch at each subdivision level.