Geometric Ornamental Design
Geometric Ornamental Design
Craig S. Kaplan
A dissertation submitted in partial fulfillment of the requirements for the degree of
Doctor of Philosophy
University of Washington
2002

In the last century, we have developed mathematical tools that let us peer into the past and analyze
historical sources of ornament with unprecedented clarity. Even when these modern tools bear
little or no resemblance to the techniques originally used to create designs, they have an undeniable
explanatory power. We can then reverse the analysis process, using our newfound understanding to
drive the synthesis of new designs.
 The great majority of ornament exhibits some degree of symmetry. The reason must in part be
The great majority of ornament exhibits some degree of symmetry. The reason must in part be
tied to the practicalities of fabricating ornament. As a simple example, fabrics and wallpapers are
printed from cylindrical templates, so their patterns will necessarily repeat in at least one direction.
Looking more at the human experience of ornament, there is also a significant neurological and
psychological basis for our appreciation of symmetry.
 Trigonometry is the study of the relationships between parts of triangles. Triangles exist in absolute
Trigonometry is the study of the relationships between parts of triangles. Triangles exist in absolute
geometry and can therefore be studied using absolute trigonometry. Bolyai first described some of
the properties of absolute triangles; his work was later expanded upon by De Tilly [14, Page 113].
 The important mathematical spaces in the present work are the parabolic, the hyperbolic, and
The important mathematical spaces in the present work are the parabolic, the hyperbolic, and
the spherical planes. We know from Kay’s presentation [97] that each of these planes has a notion
of distance, defined both formally in the axioms of geometry and concretely in the models.
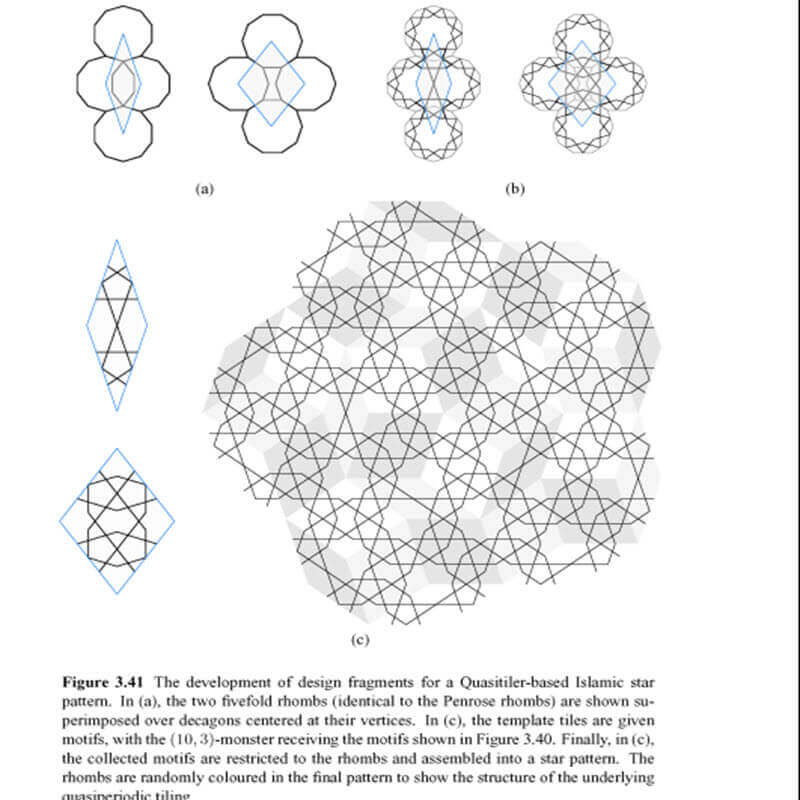 The rise and spread of Islamic culture from the seventh century onward has provided us with history’s
The rise and spread of Islamic culture from the seventh century onward has provided us with history’s
great artistic and decorative traditions. In a broad swath of Islamic rule, at one time extending
across Europe, Africa, and Asia, we find artistic treasures of unrivaled beauty. Islamic art encompasses
great achievements in calligraphy, stylized floral designs, architecture, and abstract geometric
patterns.
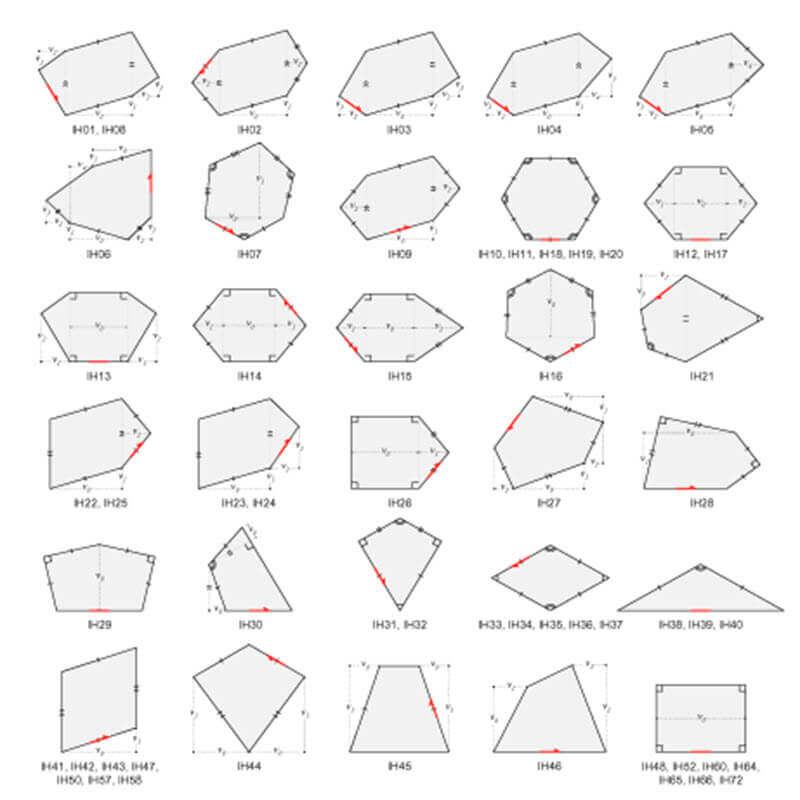 A design is a collection of line segments in the plane that do not intersect each other except
A design is a collection of line segments in the plane that do not intersect each other except
possibly at their endpoints. We may regard such a collection as an infinite planar map. The map
consists of a set of vertices, each of which has a position in the plane, and a set of edges that
connect pairs of vertices. The valence of a vertex is the number of edges that have it as an endpoint.
In the periodic case, this planar map can be conveniently represented by its restriction to a single
translational unit.
 To create a final motif, we will need to truncate every one of these rays somewhere along its
To create a final motif, we will need to truncate every one of these rays somewhere along its
length. Because the goal is to create unbroken strands, every ray will have to be truncated where it
meets some other ray, either creating a bend, or occasionally an unbroken straight line segment. If
every ray meets up with some other ray, we have a complete motif. Based on this description, we
can specify a motif by giving a pairing of the rays, a set of unordered pairs of rays in which each ray
appears exactly once. The ultimate goal of any inference algorithm is then to choose from among
all possible pairings for the one that best satisfies some sort of aesthetic goal.
 The construction of star patterns is controlled by a set of parameters: the notation describing the
The construction of star patterns is controlled by a set of parameters: the notation describing the
tiling (which includes the symmetry group [p, q], multipliers mA, mB, and mC, and so on), and the
parameters that assign motifs to the tile shapes. Let us extract from this collection the numbers p
and q, and lump all remaining parameters together into a set S.
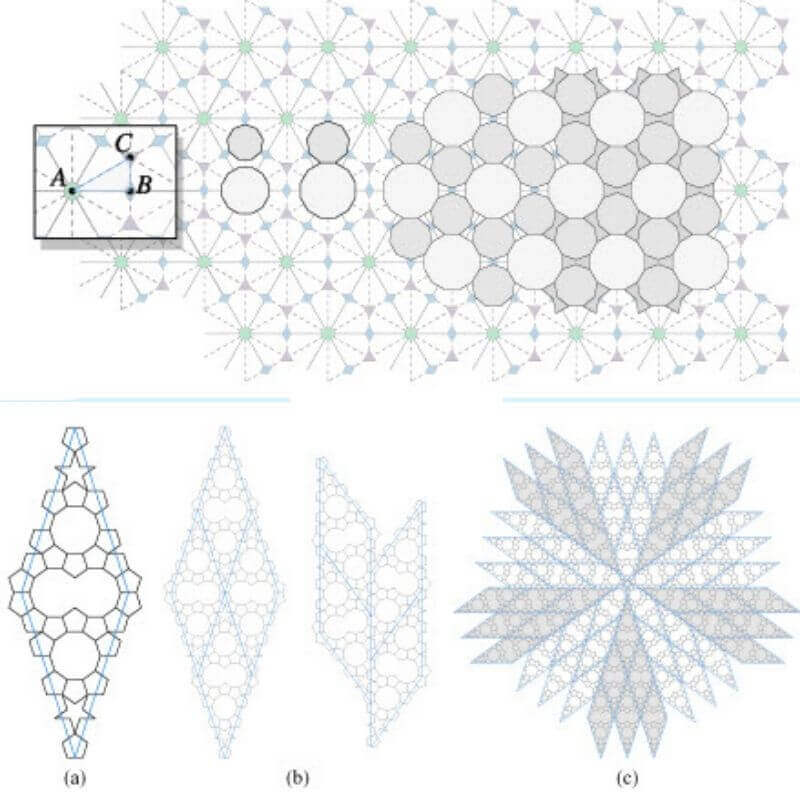 Conventionalization plays an important role in Islamic star patterns. A star pattern is not always
Conventionalization plays an important role in Islamic star patterns. A star pattern is not always
depicted as an isolated arrangement of geometric forms. Frequently, the polygonal regions defined
by the lines of a star pattern are filled not with solid colors, but with elegant floral designs that
extend more or less to the boundary of the region.
 Finally, note that when multiple transitions are chained together, it has been assumed that the
Finally, note that when multiple transitions are chained together, it has been assumed that the
chaining is done through simple concatenation. This approach limits the aesthetic range of interpolation.
In the temporal case, the passage through a gateway tiling may be continuous but exhibit a
jarring derivative discontinuity.



























Comments
Felsager
Parakeet is an excellent tool for such research. I think this paper adds more to such extension in Grasshopper 3D.