Minimal surfaces are defined as surfaces with zero mean curvature. Minimal surfaces may also be characterized as surfaces of minimal surface area for given boundary conditions.

[1]

A plane is a trivial minimal surface, and the first nontrivial examples (the catenoid and helicoid) were found by Meusnier in 1776.

A surface can be parameterized using an isothermal parameterization. The term “minimal surface” is used because these surfaces originally arose as surfaces that minimized total surface area subject to some constraint.

[2]

Physical models of area-minimizing minimal surfaces can be made by dipping a wire frame into a soap solution, forming a soap film, which is a minimal surface whose boundary is the wire frame.

[3]

However, the term is used for more general surfaces that may self-intersect or do not have constraints.

[4]

For a given constraint there may also exist several minimal surfaces with different areas (for example, see minimal surface of revolution): the standard definitions only relate to a local optimum, not a global optimum.

Minimal surfaces can be defined in several equivalent ways in R3. The fact that they are equivalent serves to demonstrate how minimal surface theory lies at the crossroads of several mathematical disciplines, especially differential geometry, calculus of variations, potential theory, complex analysis and mathematical physics.

[5]

Gyroids are a type of minimal surface that have cropped up in the design of microparticles for drug delivery.

For some two-dimensional shapes, it is easy to find geodesics that close up into a finite loop. Take, for example, a doughnut surface — not even necessarily a nicely rounded, symmetric doughnut, but one with bumps and irregularities.

[6]

Dip a curved wire frame into a soap solution, or blow a soap bubble, and the liquid quickly forms the surface with the least possible area.

The geometry of these “minimal” surfaces has occupied mathematicians for hundreds of years, and it arises in subjects from architecture, where it inspires the design of roofs and other structures, to the creation of microparticles for drug delivery.

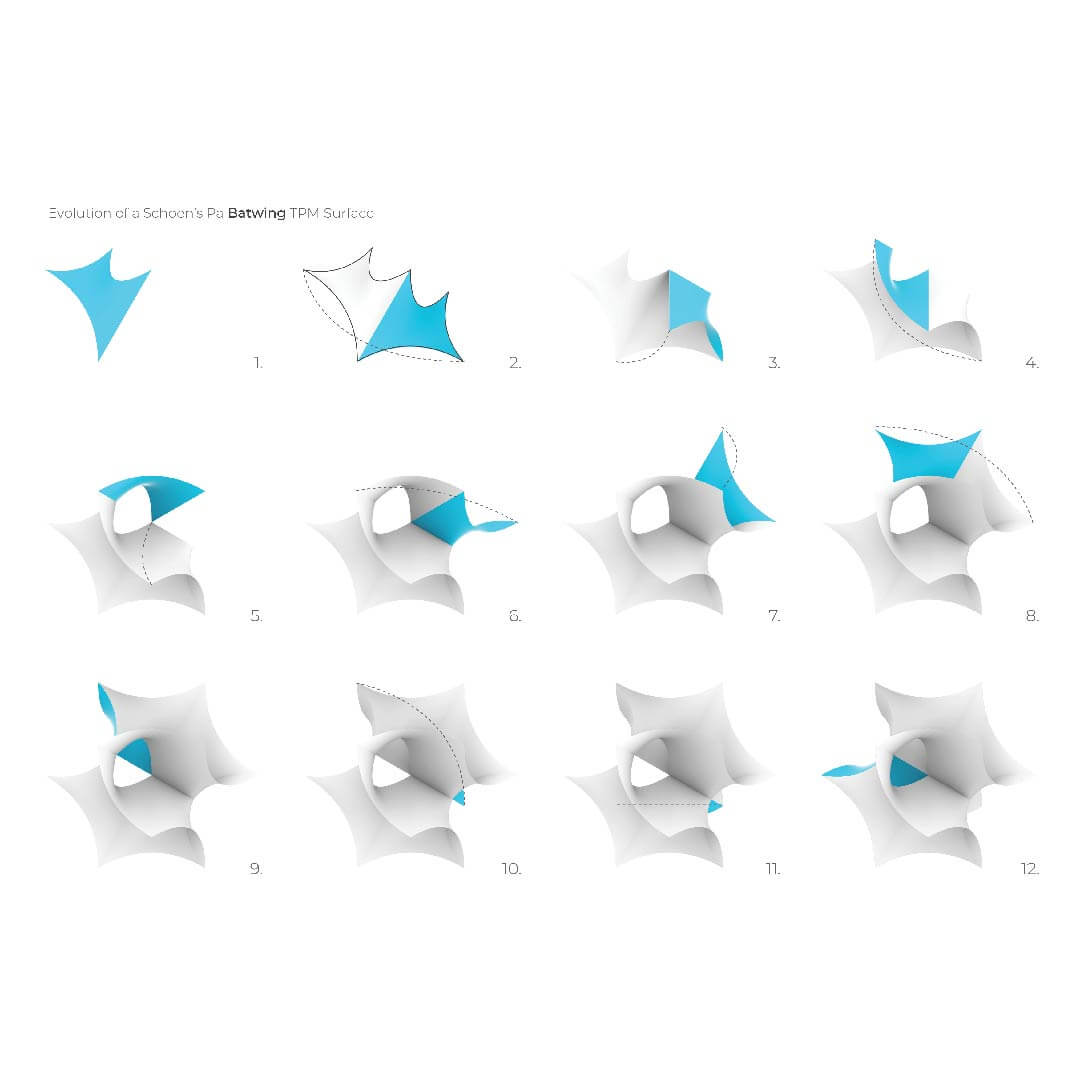Text Source: wolfram.com / Minimal Surface
quantamagazine.org / Math Duo Maps the Infinite Terrain of Minimal Surfaces

Video Source:

1- FREI OTTO – MODELING WITH SOAP FILMS/ Youtube/Frei Otto Film

2- https://vimeo.com/269711262
Porifera – 3D-printed ceramic jewelry inspired by glass sponges/ Nervous System/ Nervous System

3- Eva Hild/Youtube/ Eva Hild

4- Eva Hild at Nancy Margolis Gallery/ Youtube/ galleryIntell

5- EVA HILD/ Youtube/ Nätverkstan Medialab

6- Computing Minimal Surfaces with Differential Forms (SIGGRAPH 2021)/ SIGGRAPH/Albert Chern

7- Minimal Surface Lightbulbs/ Youtube/ DaveMakesStuff/ Instagram:@davemakesstuffbc

8- Six Minimal Surface Vases/ Youtube / DaveMakesStuff/ Instagram:@davemakesstuffbc

9- Collapse of Soap bubble catenoid in slow motion/Youtube/ SoapbubbleDK

10- D1 – Soap bubble process film/ Youtube/Sumayya Golam

11- Final Minimal Surface Experimentation/Youtube/C Cubed Media

12- Minimal Surface from Edges/ Youtube/ Rhino Grasshopper

13- Minimal Surface From Edges/ Youtube/ Rhino Grasshopper

14- Minimal Surface Installation/ Youtube/ Rhino Grasshopper