Origami Structures
 Origami, the ancient art of folding paper, has recently emerged as a method for creating deployable and reconfigurable engineering systems. These systems tend to be flexible because the thin sheets bend and twist easily. We introduce a new method of assembling origami into coupled tubes that can increase the origami stiffness by two orders of magnitude. The new assemblages can deploy through a single flexible motion, but they are substantially stiffer for any other type of bending or twisting movement. This versatility can be used for deployable structures in robotics, aerospace, and architecture. On a smaller scale, assembling thin sheets into these tubular assemblages can create metamaterials that can be deployed, stiffened, and tuned.
Origami, the ancient art of folding paper, has recently emerged as a method for creating deployable and reconfigurable engineering systems. These systems tend to be flexible because the thin sheets bend and twist easily. We introduce a new method of assembling origami into coupled tubes that can increase the origami stiffness by two orders of magnitude. The new assemblages can deploy through a single flexible motion, but they are substantially stiffer for any other type of bending or twisting movement. This versatility can be used for deployable structures in robotics, aerospace, and architecture. On a smaller scale, assembling thin sheets into these tubular assemblages can create metamaterials that can be deployed, stiffened, and tuned.
 To model the stiffness and mass of origami, we use a bar and hinge approach that provides insight into the structural behavior of the origami assemblages. It captures three fundamental physical behaviors: bending along fold lines, bending of initially flat panels, and stretching and shearing of panels. The simplicity of the bar and hinge model allows for straightforward implementation and versatility where tubes can be coupled and analyzed as more complex assemblages.
To model the stiffness and mass of origami, we use a bar and hinge approach that provides insight into the structural behavior of the origami assemblages. It captures three fundamental physical behaviors: bending along fold lines, bending of initially flat panels, and stretching and shearing of panels. The simplicity of the bar and hinge model allows for straightforward implementation and versatility where tubes can be coupled and analyzed as more complex assemblages.
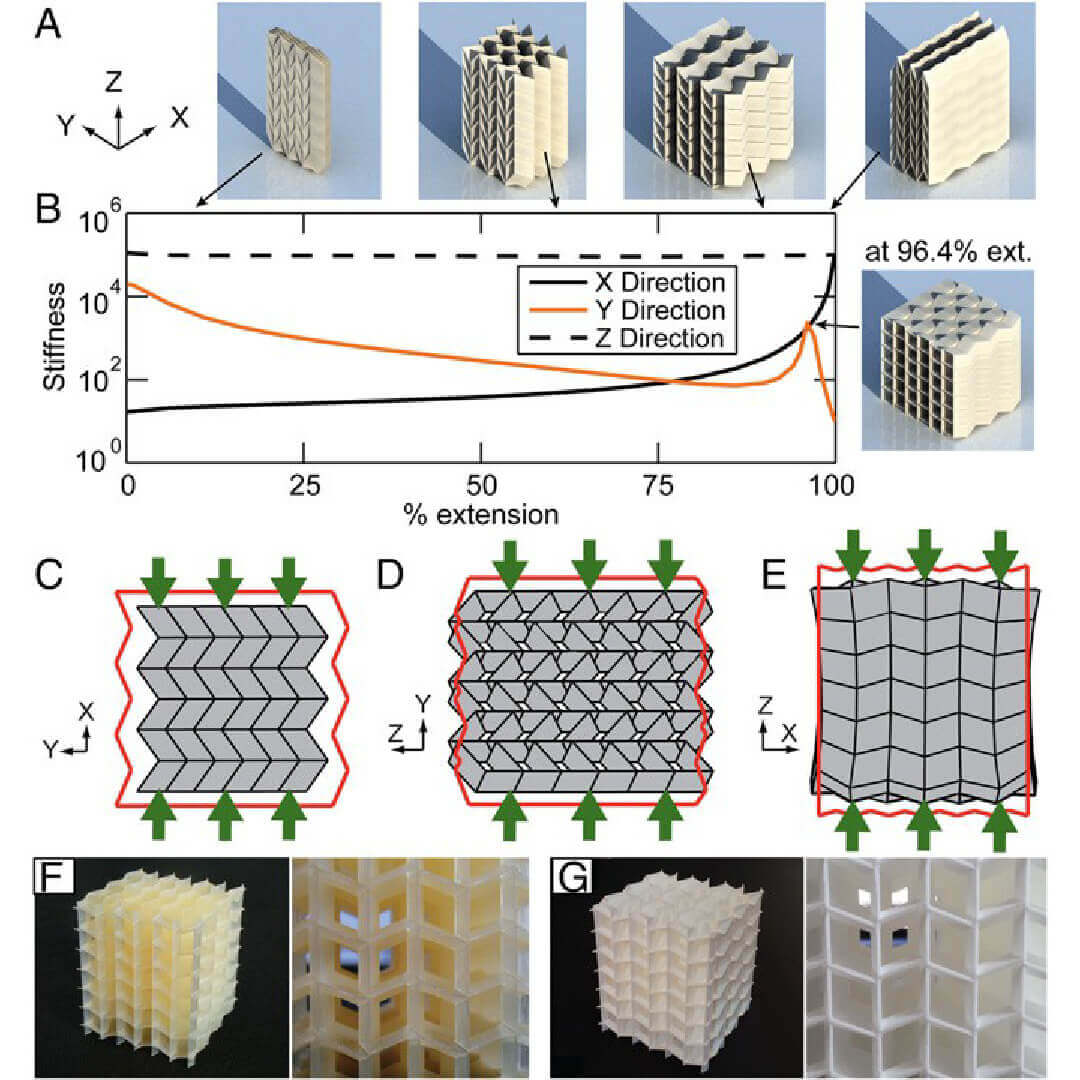 The zipper, aligned, and internally coupled tube systems can be applicable as deployable cantilever structures when restrained on one end. At the supported end all nodes are fully fixed, whereas a total load of 1 is distributed on the other end of the structure. When used as cantilevers, the tubes exhibit behavior similar to that of an I-beam, wherein the second moment of area (or area moment of inertia) is increased by distributing material away from the centroid. The aligned and internally coupled tube systems often experience squeezing-type deformations when loaded on one end, whereas the zipper-coupled tubes experience more uniform bending deformations.
The zipper, aligned, and internally coupled tube systems can be applicable as deployable cantilever structures when restrained on one end. At the supported end all nodes are fully fixed, whereas a total load of 1 is distributed on the other end of the structure. When used as cantilevers, the tubes exhibit behavior similar to that of an I-beam, wherein the second moment of area (or area moment of inertia) is increased by distributing material away from the centroid. The aligned and internally coupled tube systems often experience squeezing-type deformations when loaded on one end, whereas the zipper-coupled tubes experience more uniform bending deformations.
 The stiffness of the structures is calculated for the three Cartesian directions for different extensions. The loads are applied for each configuration, and the resultant displacements (ΔX, ΔY, and ΔZ) are calculated from the linear function F= KΔ, where F is a force vector. A quantitative stiffness of the system is then calculated as K =F=δ= 1=δ based on the maximum system displacement (δ). The zipper-coupled tubes tend to be stiffer than the other two systems and have a greater stiffness when closer to full extension. The internally coupled tubes tend to be stiff for Z-direction loading and when locked into a fixed configuration.
The stiffness of the structures is calculated for the three Cartesian directions for different extensions. The loads are applied for each configuration, and the resultant displacements (ΔX, ΔY, and ΔZ) are calculated from the linear function F= KΔ, where F is a force vector. A quantitative stiffness of the system is then calculated as K =F=δ= 1=δ based on the maximum system displacement (δ). The zipper-coupled tubes tend to be stiffer than the other two systems and have a greater stiffness when closer to full extension. The internally coupled tubes tend to be stiff for Z-direction loading and when locked into a fixed configuration.
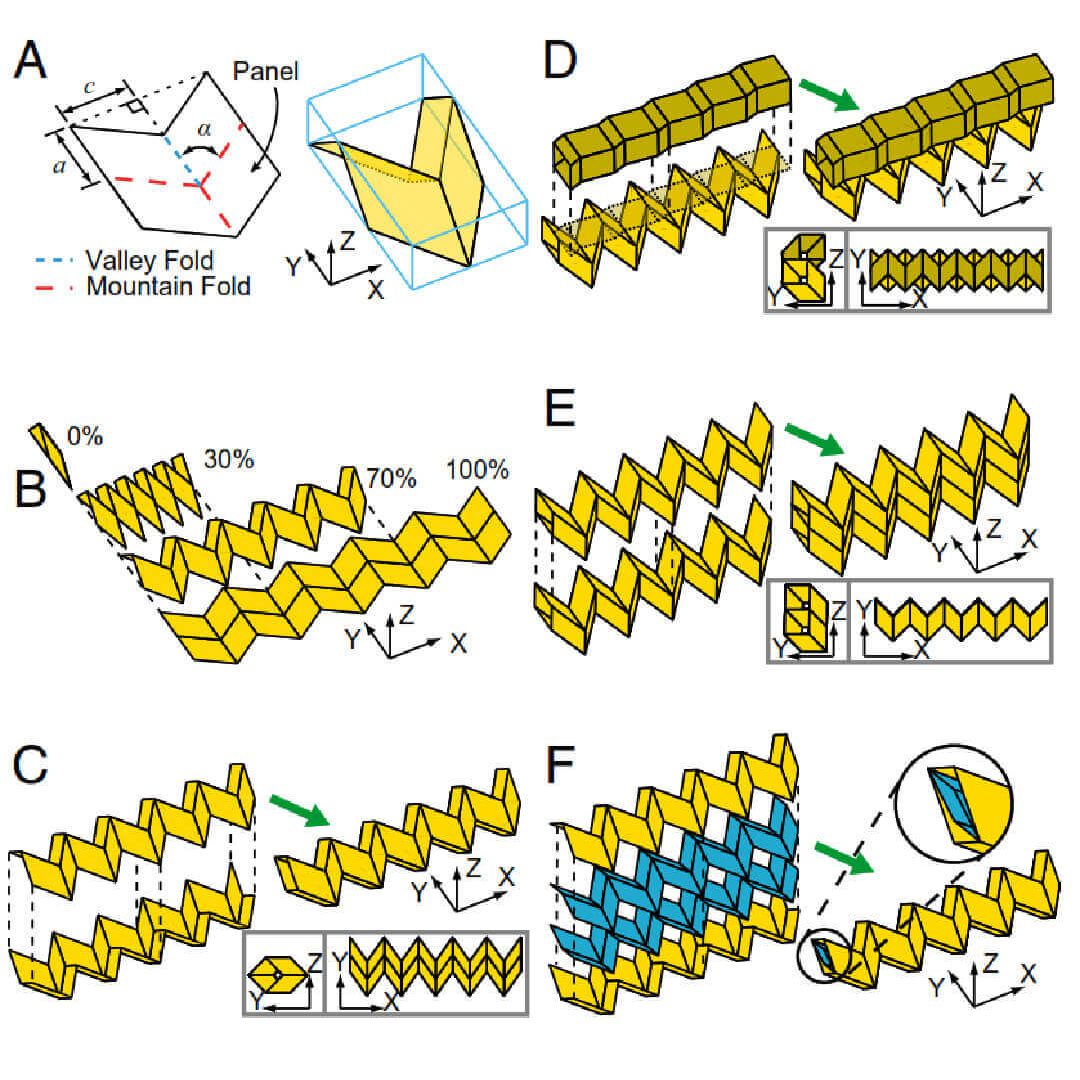 There are numerous other ways in which rigid foldable tubes can be defined, combined, and coupled. For example, a different vertex angle α and panel height a may be used with rigid and flat foldability of the system preserved. Zipper coupling can be continued in one direction to create an easily deployable slab structure resistant to out-of-plane loads; potential applications are architectural canopies, bridges, solar arrays, or synthetic materials. When the vertex angle is varied for the coupled zipper tubes, we can create arbitrarily curved systems with high out-of-plane stiffness.
There are numerous other ways in which rigid foldable tubes can be defined, combined, and coupled. For example, a different vertex angle α and panel height a may be used with rigid and flat foldability of the system preserved. Zipper coupling can be continued in one direction to create an easily deployable slab structure resistant to out-of-plane loads; potential applications are architectural canopies, bridges, solar arrays, or synthetic materials. When the vertex angle is varied for the coupled zipper tubes, we can create arbitrarily curved systems with high out-of-plane stiffness.
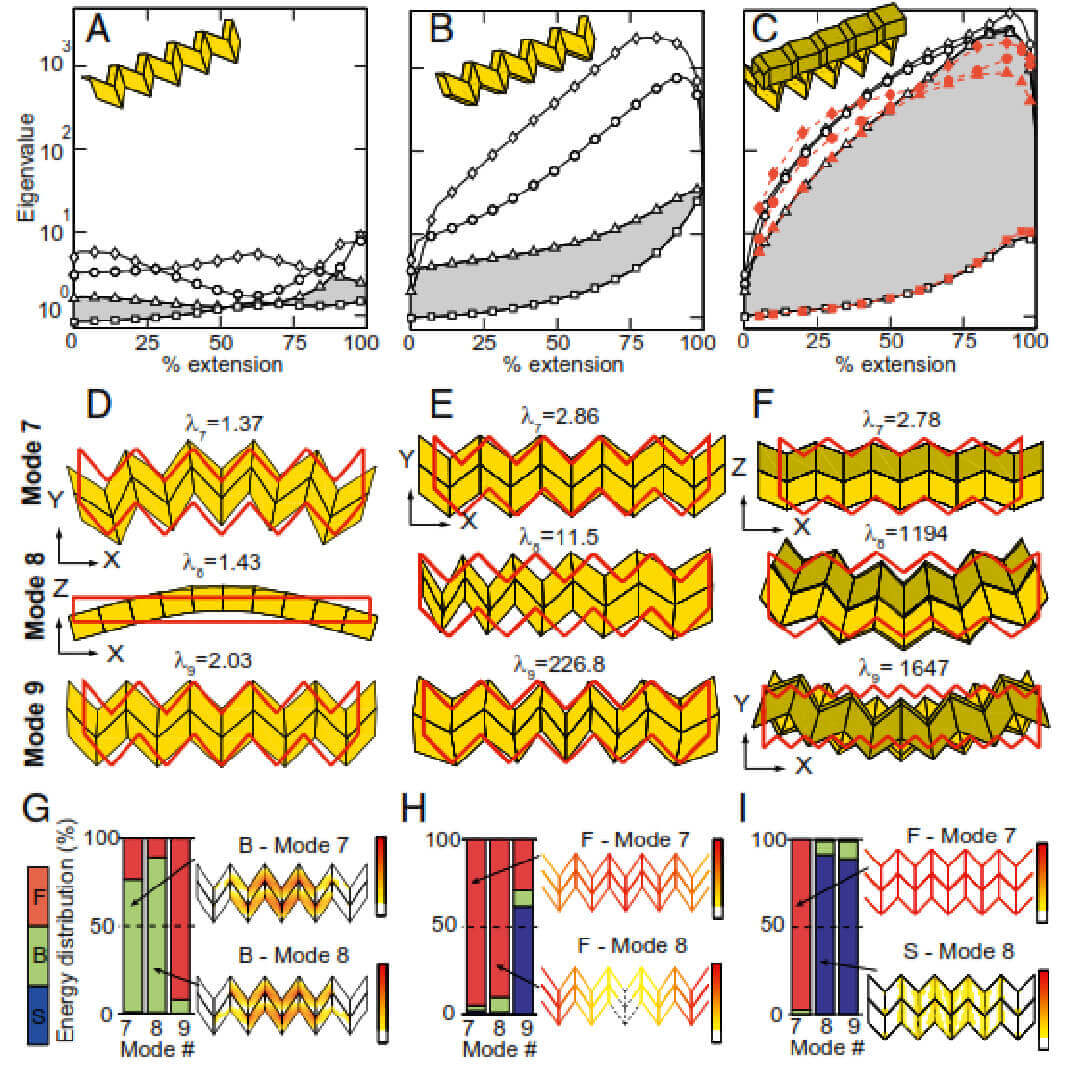 Cellular origami can permit self-assembly of engineered hierarchical materials, whose mechanical properties depend on the microstructure geometry. The structural stiffness and energy absorption properties of cellular origami can be optimized to complement and improve naturally occurring materials. Zipper-coupled tubes can be integrated with aligned or internal coupling to create layered foldable assemblages. Structures that incorporate zipper coupling inherit the large bandgap, while also retaining properties from the other coupling techniques.
Cellular origami can permit self-assembly of engineered hierarchical materials, whose mechanical properties depend on the microstructure geometry. The structural stiffness and energy absorption properties of cellular origami can be optimized to complement and improve naturally occurring materials. Zipper-coupled tubes can be integrated with aligned or internal coupling to create layered foldable assemblages. Structures that incorporate zipper coupling inherit the large bandgap, while also retaining properties from the other coupling techniques.




























Comments