Rheotomic Surfaces
Rheotomic Surfaces
Diploma Studio 10 at Westminster University School of Architecture
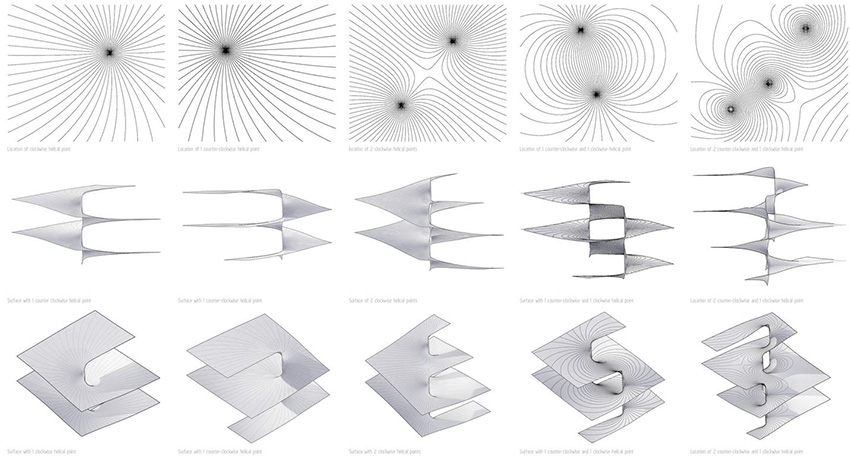
The concept Rheotomic surface’s was developed by Daniel Piker and involves the mathematical generation of ‘walkable’ interconnected surfaces. With ‘Rheo’ from the Greek for flow and ‘Tomos’ meaning cut or section these surfaces make an equivalence between the geometry of the helicoid surface ad the vortex in Laplace’s equation.
Through plotting clockwise and counter-clockwise helical points in x and y on a mesh plane, a chain of real and imaginary components from complex numbers can be generated, in turn making it possible to then plot the vertical points of the helicoid. Finally to allow the surface to be connected a separate algorithm is necessary to remove the unnecessary surface excess.

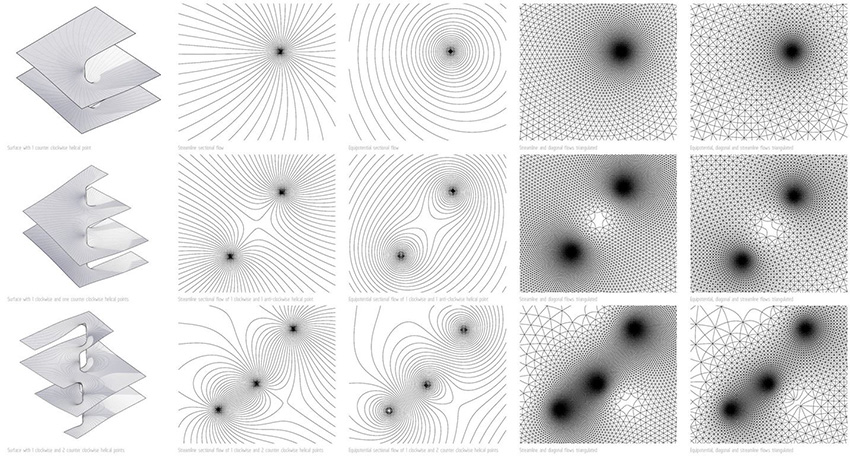
From these surfaces a variety of 2 dimensional flowlines can be produced to describe the surface geometry through sectioning. A series of different results are given depending on the combination of helical regions and the number of individual flowlines used.
Streamlines show the directional flow of the surfaces whereas equipotentials show the relationship between helical regions centres. Combining multiple flow line types produces a number of interesting patterns.

Using the generated lines of flow it is possible to map a corresponding structural grid on to the surface through curve projection. Depending on the combination of clockwise and counter clockwise helicoid regions, a variety of different results are apparent.

Structural integrity will have to be physically tested however due to the fact the grid is derived from the equation used to generate the surface it is likely that a sound result may be produced.



























Comments