Self-supporting Surfaces
Design of Self-supporting Surfaces
Etienne Vouga1, Mathias Hobinger2, Johannes Wallner3, Helmut Pottmann4
1Columbia Univ. / KAUST
2Evolute / TU Wien
3TU Graz / TU Wien
4KAUST

Figure 1: Left: Surfaces with irregularly placed holes are hard to realize as masonry, where the mortar between bricks must not be subject to tensile stresses. The surface shown here, surprisingly, has this property – it has been found as the nearest self-supporting shape from a given freeform geometry. The fictitious thrust network used in our algorithms is superimposed, with edges’ cross-section and coloring visualizing the magnitude of forces (warmer colors represent higher stresses.) Right: Curvature analysis with respect to the Airy stress surface tells us how to remesh shapes by self-supporting quad meshes with planar faces. This guides steel/glass constructions with low moments in nodes.
Self-supporting masonry is one of the most ancient and elegant techniques for building curved shapes. Because of the very geometric nature of their failure, analyzing and modeling such strutures is more a geometry processing problem than one of classical continuum mechanics.
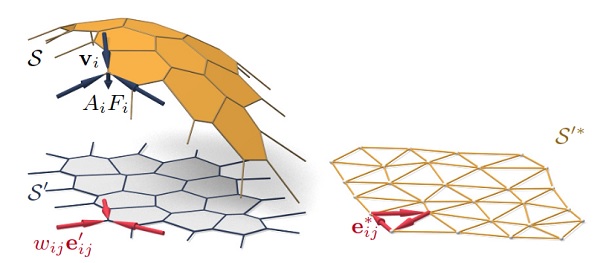
Figure 2: A thrust network S with dangling edges indicating external forces (left). This network together with compressive forces which balance vertical loads AiFi projects onto a planar mesh S 0 with equilibrium compressive forces wije 0 ij in its edges. Rotating forces by 90◦ leads to the reciprocal force diagram S 0∗ (right).
This paper uses the thrust network method of analysis and presents an iterative nonlinear optimization algorithm for efficiently approximating freeform shapes by self-supporting ones.
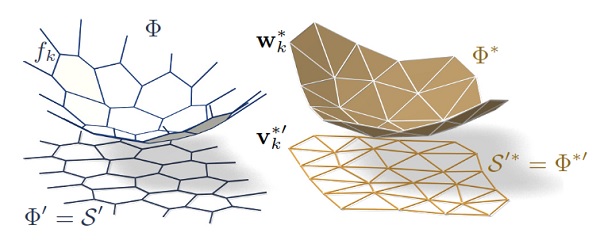
Figure 3: Airy stress potential Φ and its polar dual Φ. Φ projects onto the same planar mesh as S does, while Φ ∗ projects onto the reciprocal force diagram. A primal face fk lies in the plane z = αx + βy + γ ⇐⇒ the corresponding dual vertex is w∗ k = (α, β, −γ).
The rich geometry of thrust networks leads us to close connections between diverse topics in discrete differential geometry, such as a finite-element discretization of the Airy stress potential, perfect graph Laplacians, and computing admissible loads via curvatures of polyhedral surfaces.
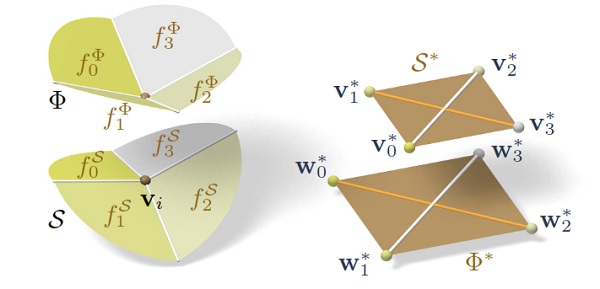
Figure 4: Mean curvature of a vertex vi of S: Corresponding edges of the polar duals S, Φ ∗ are parallel, and mean curvature according to [Pottmann et al. 2007] is computed from the vertices polar to faces adjacent to vi. For valence 4 vertices the case of zero mean curvature shown here is characterized by parallelity of non-corresponding diagonals of corresponding quads in S ∗ , Φ .
This geometric viewpoint allows us, in particular, to remesh self-supporting shapes by self-supporting quad meshes with planar faces, and leads to another application of the theory: steel/glass constructions with low moments in nodes.

Figure 5: The top of the Lilium Tower (a) cannot stand as a masonry structure, because its central part is concave. Our algorithm finds a nearby self-supporting mesh (b) without this impossible feature. (c) shows the corresponding Airy mesh Φ and reciprocal force diagram S 0∗. (d) The user can edit the original surface, such as by specifying that the center of the surface is supported by a vertical pillar, and the self-supporting network adjusts accordingly.
Vaulted masonry structures are among the simplest and at the same time most elegant solutions for creating curved shapes in building construction. For this reason they have been an object of interest since antiquity; large, non-convex examples of such structures include gothic cathedrals. They continue to be an active topic of research today.

Figure 6: A freeform surface (left) needs adjustments around the entrance arch and between the two pillars in order to be selfsupporting; our algorithm finds the nearby surface in equilibrium (right) that incorporates these changes.
Our paper is concerned with a combined geometry+statics analysis of self-supporting masonry and with tools for the interactive modeling of freeform self-supporting structures. Here “self-supporting” means that the structure, considered as an arrangement of blocks (bricks, stones), holds together by itself, with additional support present only during construction.
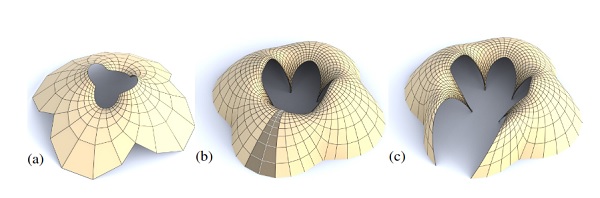

Figure 7: Interactive Edits. (a) shows a self-supporting thrust network – in fact it is a Koebe mesh as mentioned in §5. In (b) boundary conditions are defined and pillars have been added. Cutting along the highlighted edge and optimizing for the self-supporting property results in the mesh shown in (c).
Our approach is twofold: We first give an overview of the continuous case of a smooth surface under stress, which turns out to be governed locally by the Airy stress function. This mathematical model is called a membrane in the engineering literature and has been applied to the analysis of masonry before.
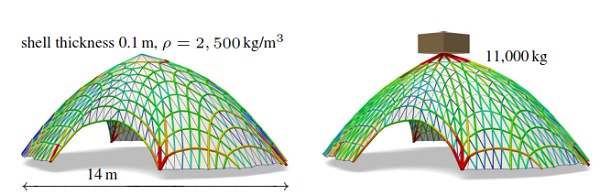

Figure 9: Stability Test. Left: Coloring and cross-section of edges visualize the magnitude of forces in a thrust network which is in equlibrium with this dome’s dead load. Right: When an additional load is applied, there exists a corresponding compressive thrust network which is still contained in the masonry hull of the original dome. This implies stability of the dome under that load.
The surface is self-supporting if and only if stresses are entirely compressive. For computational purposes, stresses are discretized as a fictitious thrust network [Block and Ochsendorf contained in the masonry structure; this network is a system of forces in equilibrium with the structure’s deadload.
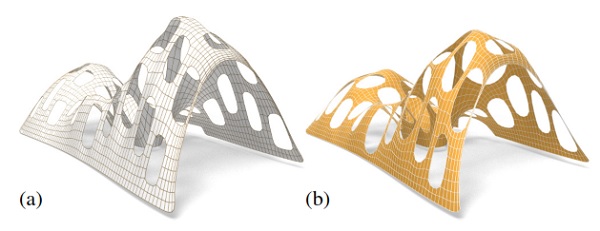
Figure 11: A mesh with holes (a) requires large deformations to both the top view and heights to render it self-supporting (b)
It can be interpreted as a finite element discretization of the continuous case, and it turns out to have very interesting geometry, with the Airy stress function becoming a polyhedral surface directly related to a reciprocal force diagram.
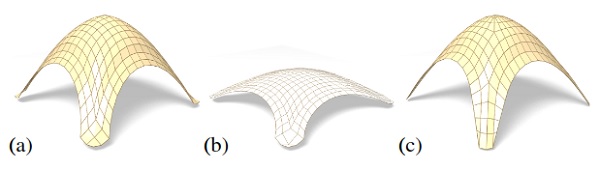
Figure 12: Directly enforcing planarity of the faces of even a very simple self-supporting quad-mesh vault (a) results in a surface far removed from the original design (b). Starting instead from a remeshing of the surface with edges following relative principal curvature directions yields a self-supporting, PQ mesh far more faithful to the original (c).
While previous work in architectural geometry was mostly concerned with aspects of rationalization and purely geometric sideconditions which occur in freeform architecture, the focus of this paper is design with statics constraints.
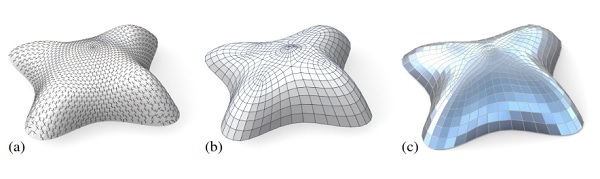
Figure 13: Planar quad remeshing of the surface of Fig. 5. (a) Relative principal directions, found from eigenvectors of (∇2φ) −1∇2 s. (b) Quad mesh guided by principal directions is almost planar and almost self-supporting. (c) Small changes achieve both properties.
Conclusion. This paper builds on relations between statics and geometry, some of which have been known for a long time, and connects them with newer methods of discrete differential geometry, such as discrete Laplace operators and curvatures of polyhedral surfaces.

Figure 14: Planar quad remeshing of the surface of Figure 6. Left: Relative principal directions. Right: The result of optimization is a self-supporting PQ mesh, which guides a momentfree steel/glass construction (interior view, see also Fig. 1).
We were able to find efficient ways of modeling selfsupporting freeform shapes, and provide architects and engineers with an interactive tool for evaluating the statics of freeform geometries.
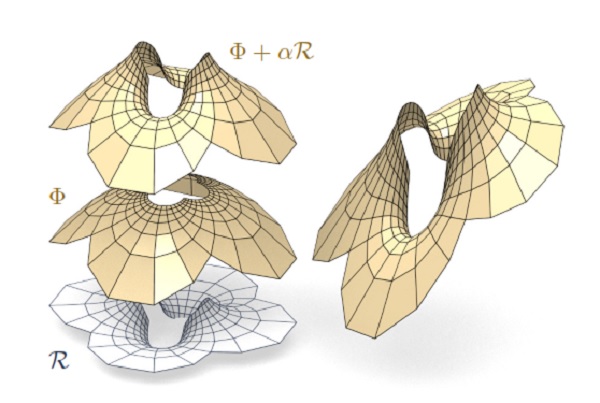
Figure 15: Left: A “Koebe” mesh Φ is self-supporting for unit dead load. An family of self-supporting meshes with the same top view is defined by Sα = Φ + αR, where R is chosen as Φ’s Christoffeldual. The right hand image shows a different example of the same connectivity.
The self-supporting property of a shape is directly relevant for freeform masonry. The actual thrust networks we use for computation are relevant e.g. for steel constructions, where equilibrium of deadload forces implies absence of moments.
This theory and accompanying algorithms thus constitute a new contribution to architectural geometry, connecting statics and geometric design.




























Comments