A space-filling curve maps a 1-dimensional space onto a higher-dimensional space, e.g., the unit interval onto the unit square.

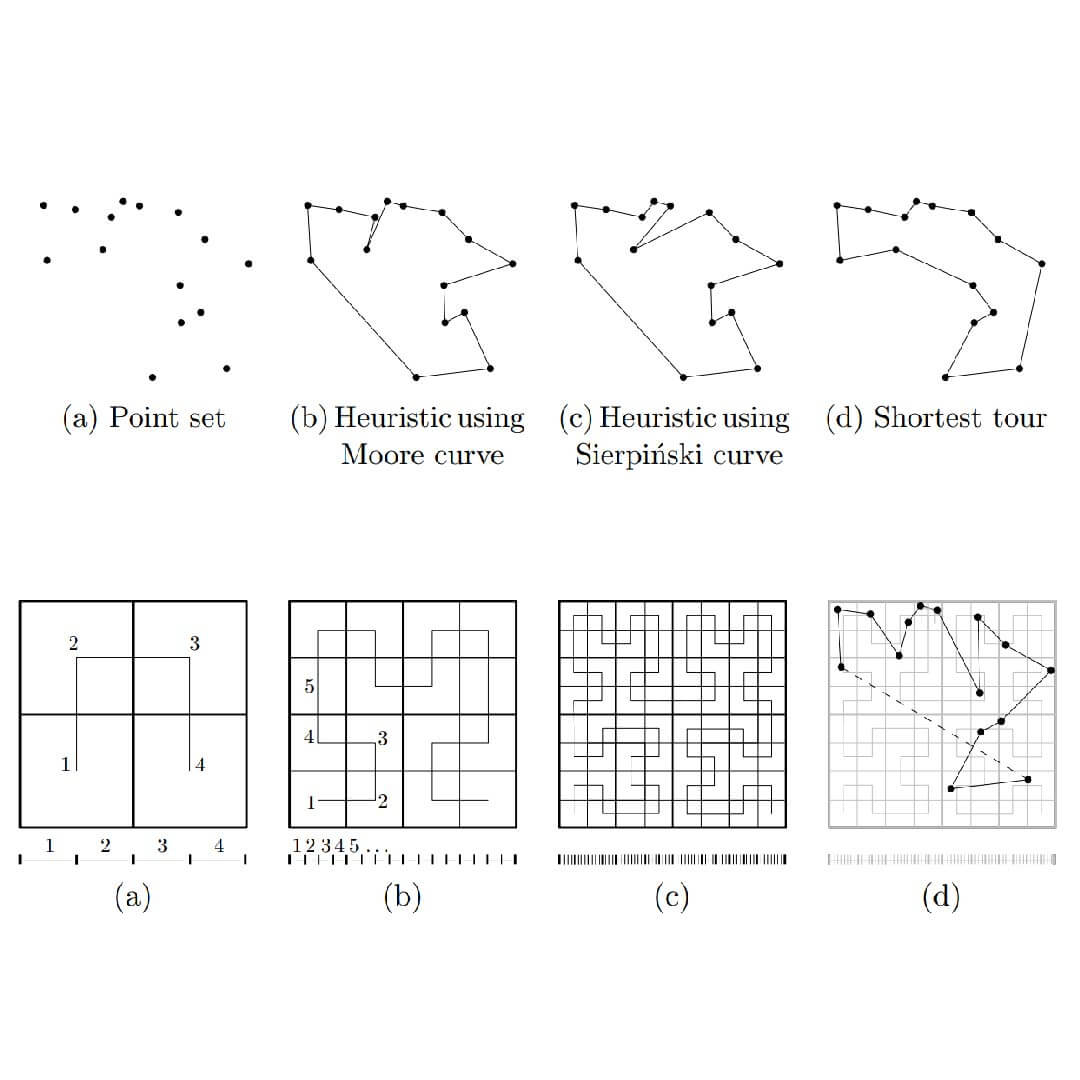
The Euclidean traveling salesperson problem is the problem of finding the shortest closed tour through a set of points.

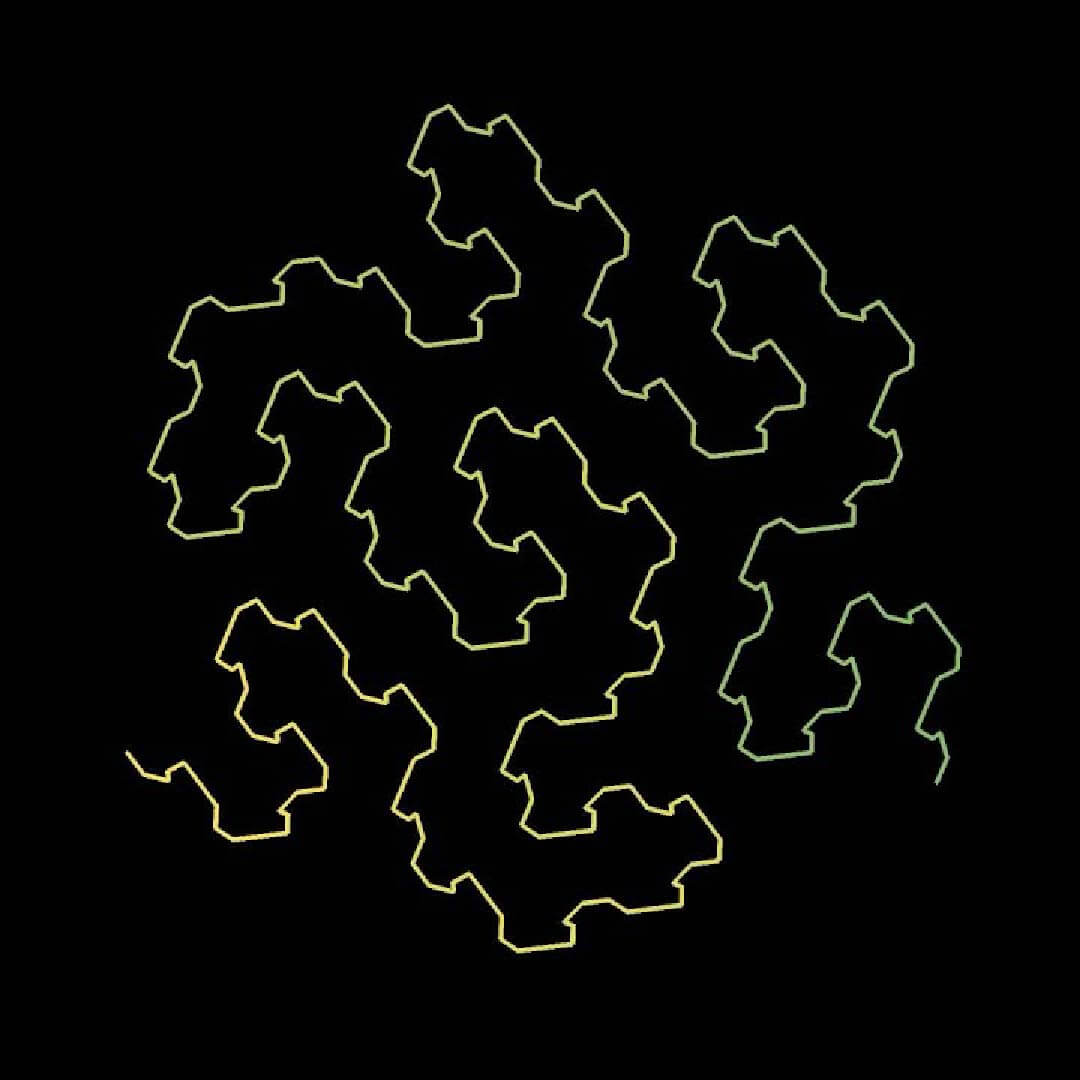In general, space-filling curves allow one to reduce higher-dimensional proximity problems, e.g., nearest neighbor search, to a one-dimensional problem.

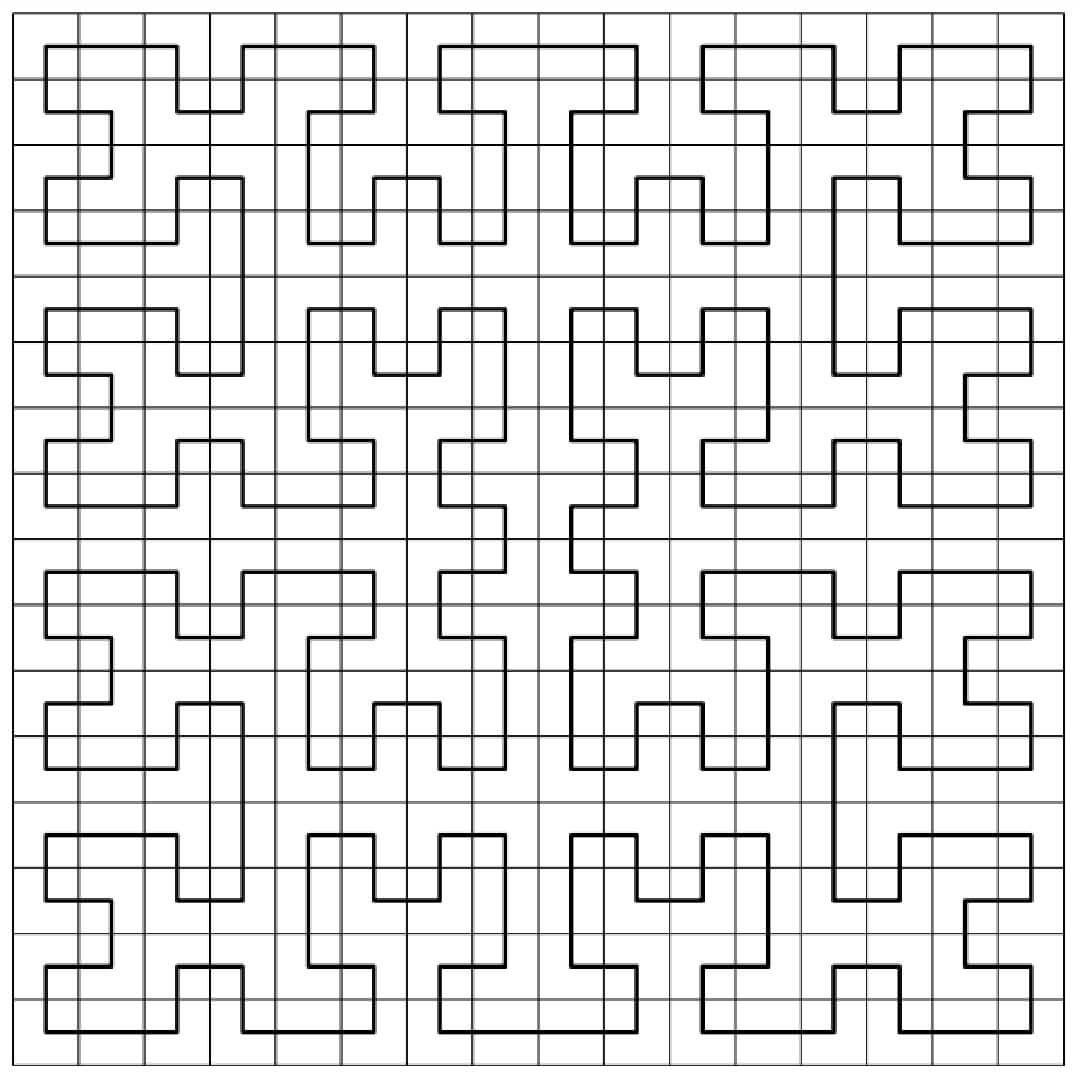Solving such a problem typically involves searching and sorting in the one-dimensional space.

A common application of space-filling curves is storage and retrieval of multi-dimensional data in a database.

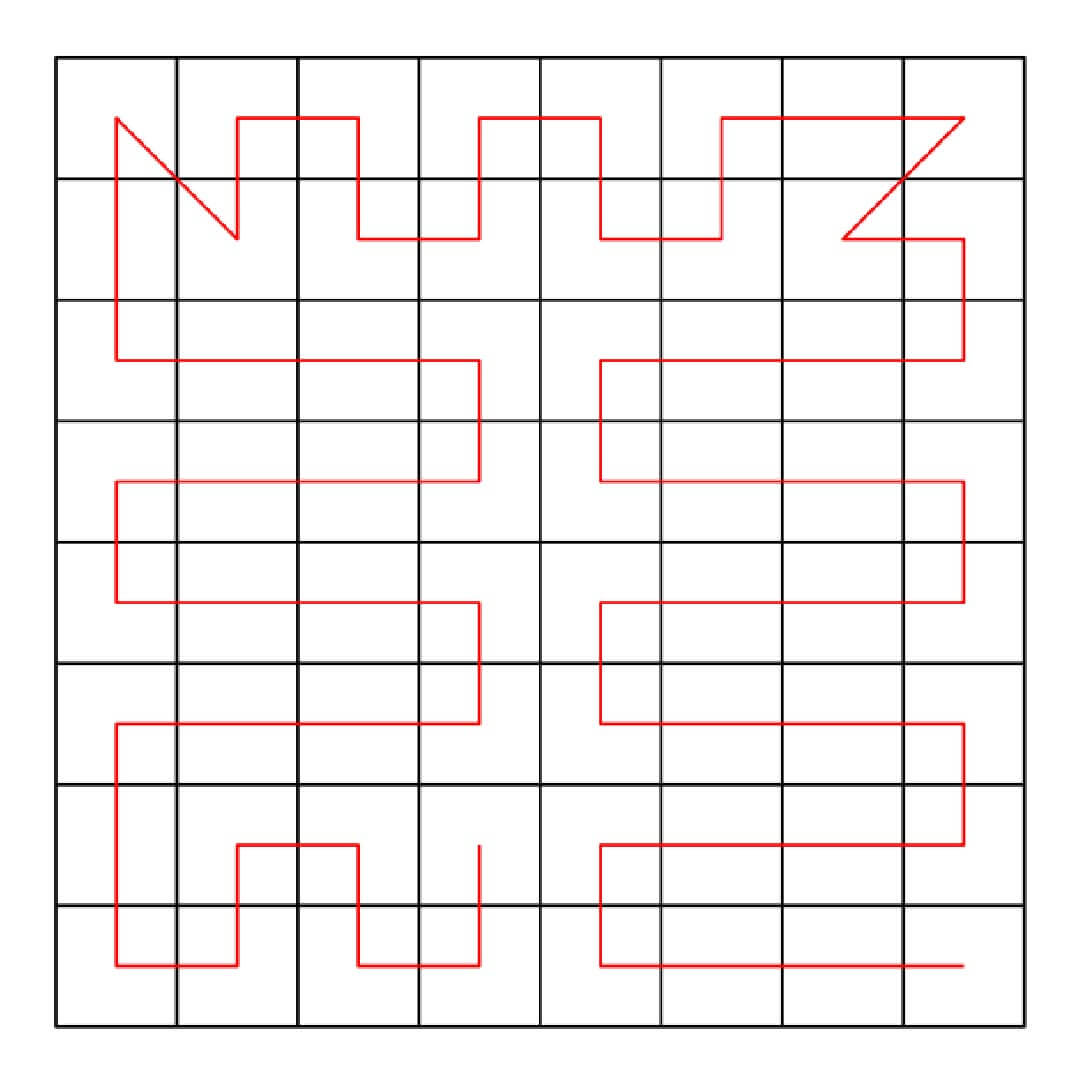Space-filling curves are also used for low-dimensional problems as in the case of the traveling salesperson problem.

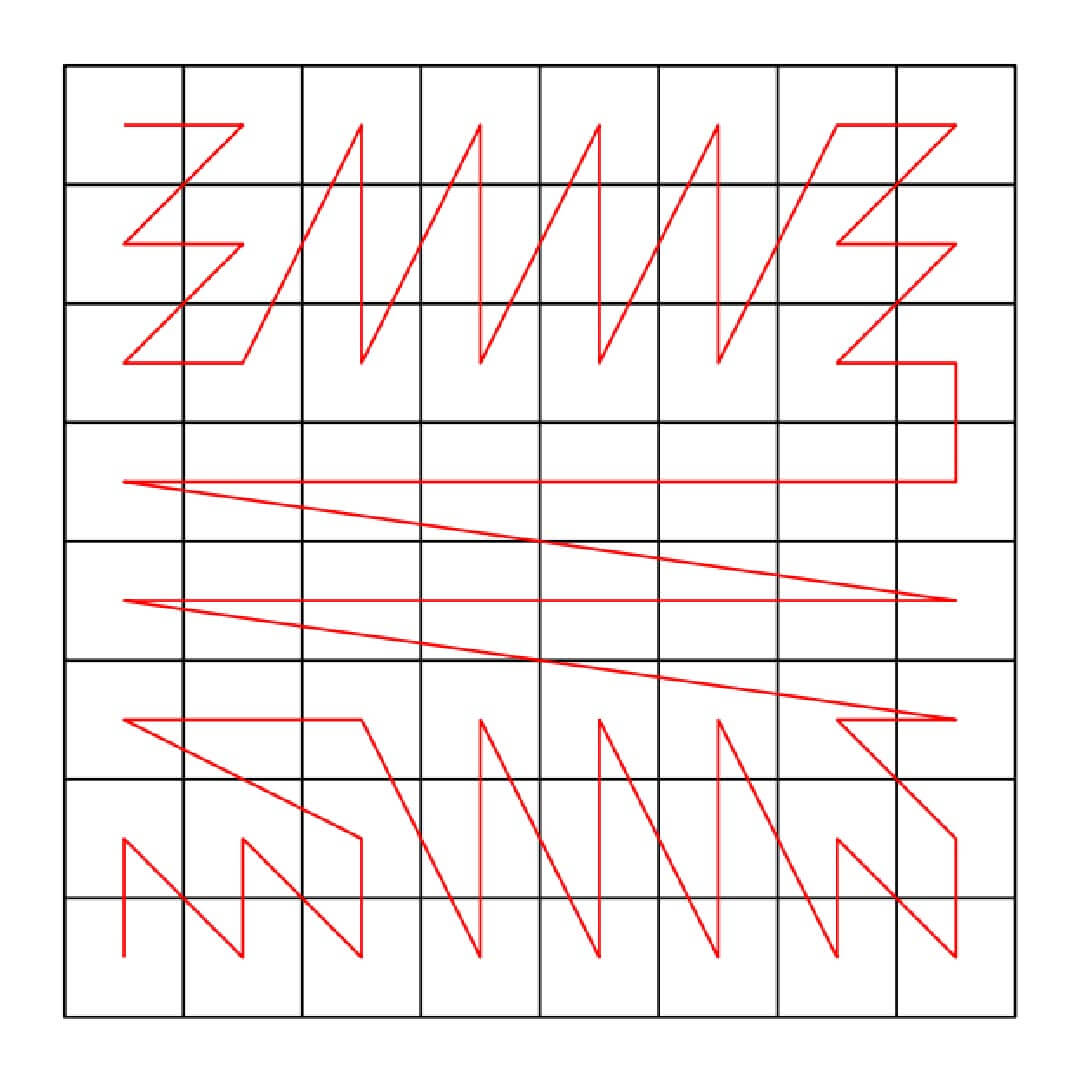For instance, they are used to index meshes for parallel and distributed computing and to organize and process raster data, e.g., images, terrains, and volumetric data.

Text Source: refubium.fu-berlin.de / Space-Filling Curves

[1]

[2]

[3]

Video Source :

1- Fractal charm: Space filling curves /Youtube / 3Blue1Brown

2-Cannon-Thurston maps /Source : Youtube / Henry Segerman

3-Unfolding The Dragon | Fractal Curve / Source : Youtube / Think Twice

4-Growth of a Self-Avoiding Fractal Curve / Source : Youtube / Jeffrey Ventrella

5-Growing Mandelbrot’s “Quartet” Curve / Source : Youtube / Jeffrey Ventrella

6-Hilbert Curve Panel / Source : Youtube / Parametric House

7-Hilbert Curve Fractal / Source : Youtube / Parametric House

Image Source :

[1]
Ricard Borrell, Juan Carlos García Cajas, Daniel Mira, Ahmed Taha, Seid Koric/ Parallel mesh partitioning
https://hal.archives-ouvertes.fr/hal-01969026/document

[2]
The Hilbert curve in two different versions, curvy and straight / Roger Antonsen

[3]
The Hilbert curve in two different versions, curvy and straight / Roger Antonsen
https://im.icerm.brown.edu/portfolio/perspectives-on-the-hilbert-curve/