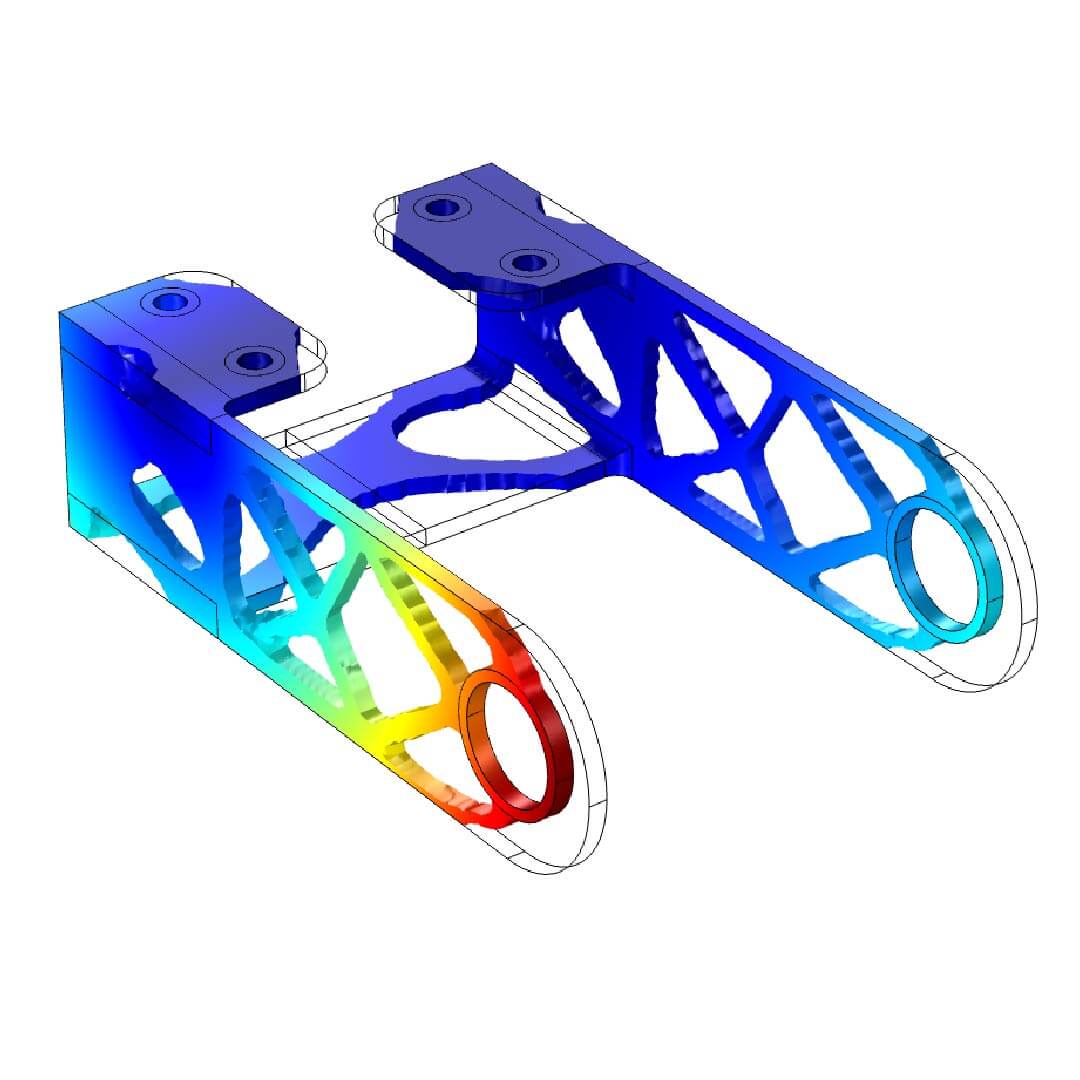
Topology Optimization
Topology optimization is a mathematical method which spatially optimizes the distribution of material within a defined domain, by fulfilling given constraints previously established and minimizing a predefined cost function.
 Topology optimization is different from shape optimization and sizing optimization in the sense that the design can attain any shape within the design space, instead of dealing with predefined configurations.
Topology optimization is different from shape optimization and sizing optimization in the sense that the design can attain any shape within the design space, instead of dealing with predefined configurations.
The conventional topology optimization formulation uses a finite element method (FEM) to evaluate the design performance.
 The design is optimized using either gradient-based mathematical programming techniques such as the optimality criteria algorithm and the method of moving asymptotes or non gradient-based algorithms such as genetic algorithms.
The design is optimized using either gradient-based mathematical programming techniques such as the optimality criteria algorithm and the method of moving asymptotes or non gradient-based algorithms such as genetic algorithms.
Topology optimization has a wide range of applications in aerospace, mechanical, bio-chemical and civil engineering.

[1]
Currently, engineers mostly use topology optimization at the concept level of a design process. Due to the free forms that naturally occur, the result is often difficult to manufacture. For that reason the result emerging from topology optimization is often fine-tuned for manufacturability.
 Adding constraints to the formulation in order to increase the manufacturability is an active field of research. In some cases results from topology optimization can be directly manufactured using additive manufacturing; topology optimization is thus a key part of design for additive manufacturing.
Adding constraints to the formulation in order to increase the manufacturability is an active field of research. In some cases results from topology optimization can be directly manufactured using additive manufacturing; topology optimization is thus a key part of design for additive manufacturing.

[2]
Solving topology optimization problems in a discrete sense is done by discretizing the design domain into finite elements.

[3]
The material densities inside these elements are then treated as the problem variables. In this case material density of one indicates the presence of material, while zero indicates an absence of material.

[4]
The earlier stated complexities with solving topology optimization problems using binary variables has caused the community to search for other options.

[5]
Topology optimization has been used by mechanical and civil engineers for many years, for example in order to minimize the amount of used material and the strain energy of structures while maintaining their mechanical strength.

[6]
The traditional solutions for structural optimization problems in buildings were determined by the use of direct search methods on an Isotropic Solid and Empty (ISE) topology.
[7]
Text Source: Topology optimization / wikipedia
Topology Optimization / sciencedirect
Video Source:
1- MX3D Printed Bridge Update 2018/ Youtube/ MX3D
2- MX3D Bridge Placement, Amsterdam 2021 / Youtube / MX3D
3- World’s first 3D printed STEEL bridge | MX3D / Youtube / Belindar Carr
4- Producing the world’s first 3D-printed bridge with robots “is just the beginning” – Joris Laarman / Youtube / Dezeen
5- Ameba Topology Optimization Software Based on Grasshopper / Youtube / Ameba
6- 3D concrete printing of a topology-optimized bridge/ Youtube/ Concrete3DLab Ghent
7- Topology-optimized concrete bridge/ Youtube/ Concrete3DLab Ghent
8- Topology optimisation of a bridge / Youtube / Jordan Burgess
9- Topology optimization for additive manufacturing Part 1/4/ Youtube/ Jun Wu
10- Topology optimization for additive manufacturing Part 4/4/ Youtube/ Jun Wu
11- 3F3D – Form Follows Force with 3D Printing / Youtube / Bayu Prayudhi



























Comments