Transformable Structures
Transformable Structures and their Architectural Application
Sam Bouten
Department of Structural Engineering Chairman: Prof. Dr. Ir. Luc Taerwe
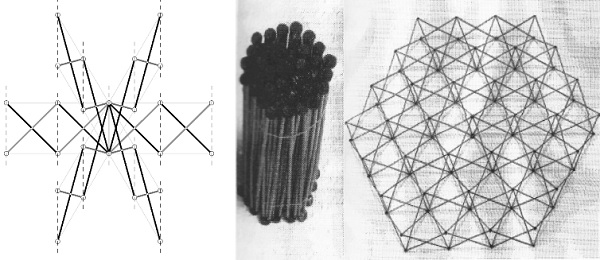
Fig 2.4a Hexa-triangular grid array
Fig 2.4b (Escrig F. 1991b)
The field of transformable structures is remarkably varied since it transcends the borders of conventional disciplines and inscribes itself into the modern notion of adaptivity. The main aim of this thesis is to provide insight in the design of transformable structures on an architectural scale.
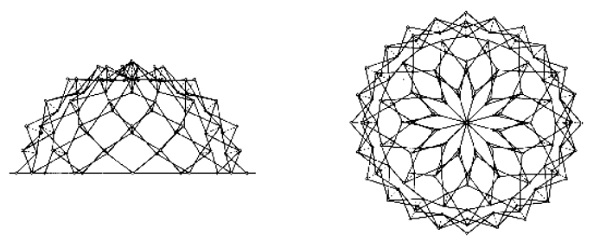
Fig 2.19 Lamella dome (Escrig F. 1988)
The term itself, transformable structure, is an oxymoron: structure is what gives static shape to systems, while transformable is a word more at home in the world of the shifting and the unstable.
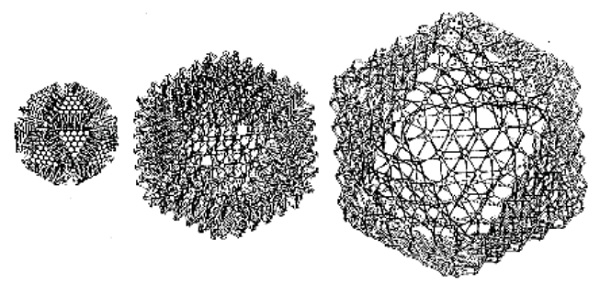
Fig 2.27 Expansion of icosahedron from angulated units (Hoberman C. 1990a)
It’s between these two worlds that transformable structures strike a balance, looking for a trade-off between the mechanical and static qualities.

Fig 2.29 Emilio Pérez Piñero and his design for a deployable theatre, oblique grid from polar units
In the transformation phase, controlled movements must be potentiated, but once the mechanism is locked in place, the resulting structure must be rigid and secure in its use.

Fig 2.34 Expansion of triangulated geodesic dome from angulated units (Hoberman C. portfolio)
The terms structure and mechanism (or linkage) will hence be used freely in the thesis, sometimes referring to the very same geometries, depending on the state they are in.

Fig 3.17 Hexagonal Resch pattern
Fig 3.18 Large-scale folded Resch pattern
The fact that this field of study is located at an intersection point of many other domains makes it very diverse, and many points of view need to be reconciled in any transformable design.

Fig 3.17 Variations on Resch pattern (Piker D. 2009a)
Not only structural and kinematical aspects, but also three-dimensional geometric patterning, transport and actuation play a part.

Fig 3.24 Radial shelter from variable pattern (Schenk M. 2012, project by Ming Tang)
In short, thinking about transformable structures inherently includes the fourth dimension of time,a factor often minimalized in the building industry, where static and unchanging constructions rule.

Fig 3.27a Acoustic panels from Resch pattern
Fig 3.27b Actuation system (RVTR)
Although transformable structures have been used throughout history – mostly on the fringes of architectural culture – their more recent popularization inscribes itself into a wider paradigm shift, where a dynamic lifestyle and durability are two key notions.

Fig 3.30 Wooden facets on fabric (Elisa Strozyk)
Transformable structures can offer dynamic answers to modern problems, such as deployment for creating temporary spaces, responsiveness to climatic influences, and change of use. The design of transformable structures then is the design of change.

Fig 4.1 Transformation of Jitterbug mechanism
The transformable will undergo additional stresses when it is in phases of geometric incompatibility. If these stresses occur only at intermediate phases of the deployment or transformation, it is said that there is a snap-through effect: an additional amount of force is needed to deform the system and cause it to snap from one phase to the next.

Fig 4.16 Pyramidal dipoligonid with facetted faces (Verheyen H. 1989)
This phenomenon can even be of an added advantage, as Zeigler H. (1976) first used these stresses to attain a self-locking mechanism: the structure is fixed easily into its deployed state.

Fig 7.24 Model suspended from cables for actuation (Hoberman C. portfolio)
The joint-to-joint type has been used in the work of Wohlhart K. and Calatrava Valls S. (1981), but a more thorough analysis of the geometric possibilities and structural use of the arrays had been lacking. The overlap array, in turn, is novel and shows promising structural advantages.

The numerical relationships between the elements lengths and polar angle of a Sarrus module have been derived and, using the resulting equations, a parametric tool was developed in Grasshopper software. This tool can be used to generate both flat and polar arrays.
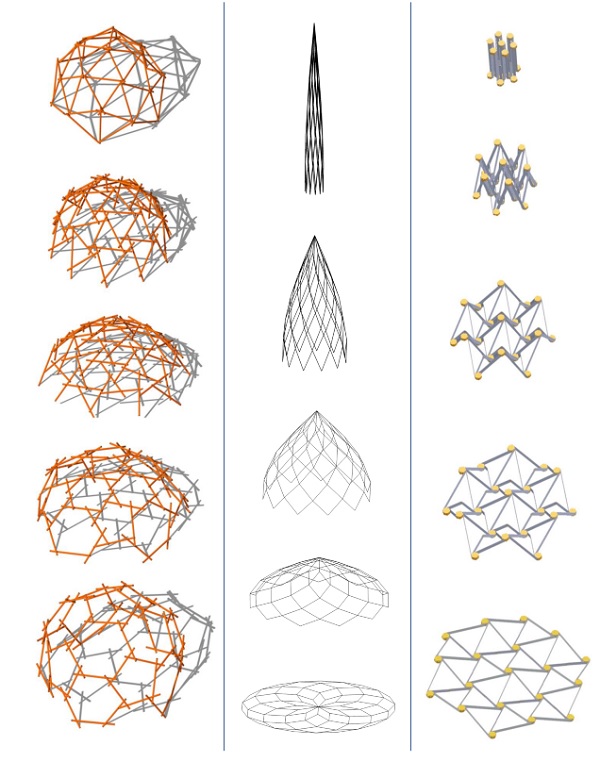
An additional dependent mobility was noticed in physical models of joint-to-joint arrays and first attempts at describing this mobility have been made.
Furthermore, various solutions for removing the dependent mobility in order to have a more controlled deployment have been offered.




























Comments