Geometry of Structures
The constrained geometry of structures:
Optimization methods for inverse form-finding design
Pierre Cuvilliers
Submitted to the Department of Architecture
in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy in Architecture: Building Technology
Massachusetts Institute of Technology
May 2020

This dissertation by Pierre Cuvilliers aims to improve form-finding workflows by giving more control on the obtained shapes to the designer. Traditional direct form-finding allows the designer to generate shapes for structures that need to verify a mechanical equilibrium when built; however, it produces shapes that are difficult to control.
 This dissertation shows how the design of constrained structural systems is better solved by an inverse form-finding process, where the parameters and initial conditions of the direct form-finding process are automatically adjusted to match the design intent. By defining a general framework for the implementation of such workflows in a nested optimizer loop, the requirements on each component are articulated.
This dissertation shows how the design of constrained structural systems is better solved by an inverse form-finding process, where the parameters and initial conditions of the direct form-finding process are automatically adjusted to match the design intent. By defining a general framework for the implementation of such workflows in a nested optimizer loop, the requirements on each component are articulated.
 The inner optimizer is a specially selected direct form-finding solver, the outer optimizer is a general-purpose optimization routine. This is demonstrated with case studies of two structural systems: bending-active structures and funicular structures.
The inner optimizer is a specially selected direct form-finding solver, the outer optimizer is a general-purpose optimization routine. This is demonstrated with case studies of two structural systems: bending-active structures and funicular structures.
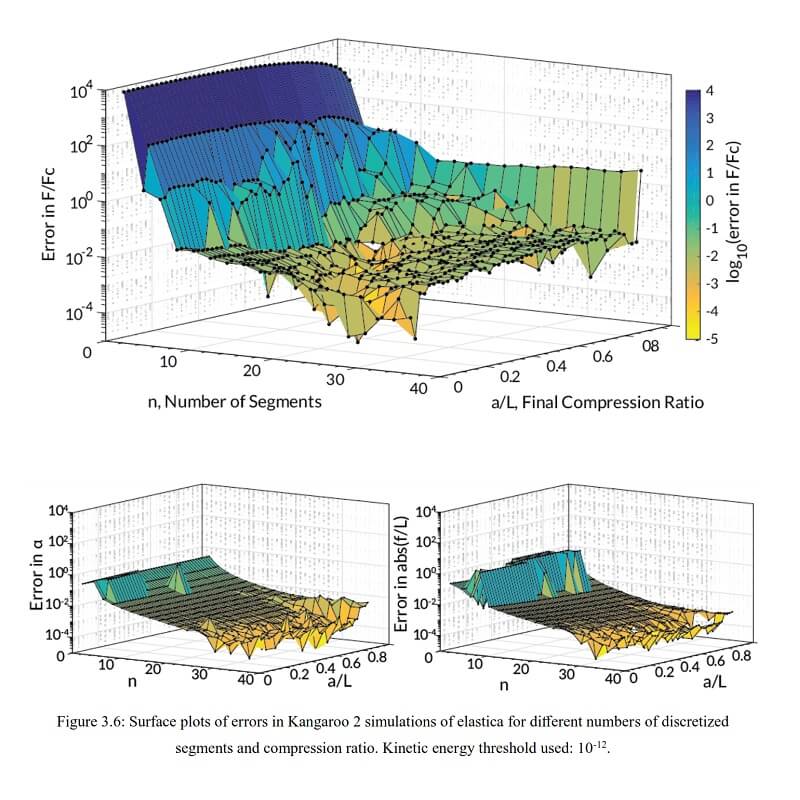
These two systems that can lead to efficient covering structures of long spans. For bending-active structures, the performance (speed, accuracy, reliability) of direct form-finding solvers is measured. Because the outer optimization loop in an inverse form-finding setup needs to rely on a robust forward simulation with minimal configuration, author finds that general-purpose optimizers like SLSQP and L-BFGS perform better than domain-specific algorithms like dynamic relaxation.
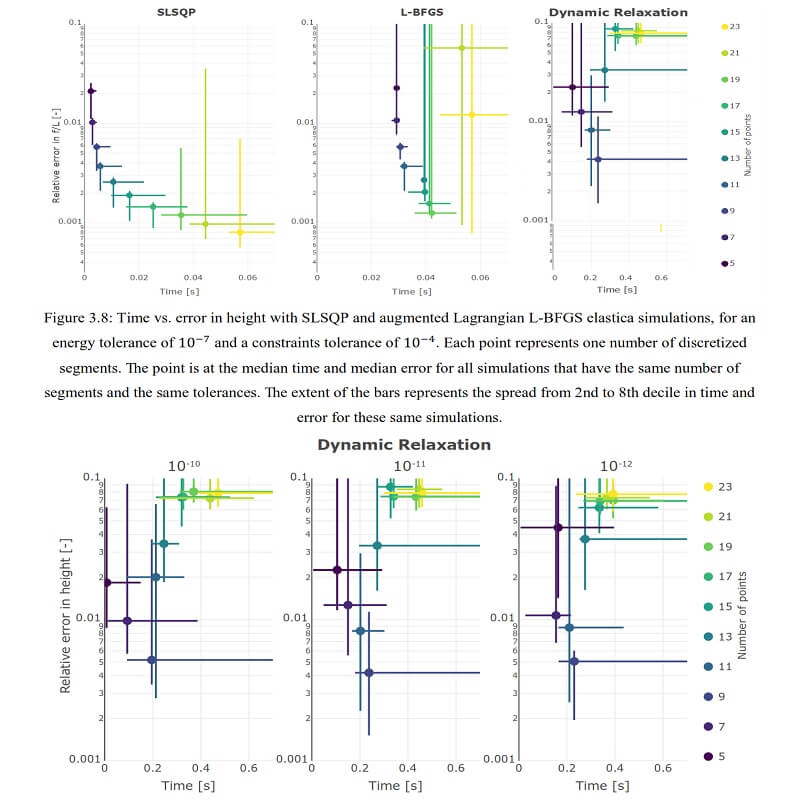 Using this insight, an inverse form-finding workflow is built and applied with a closest-fit optimization objective. In funicular structures, this dissertation first focuses on a closest-fit to target surface optimization, giving closed-form formulations of gradients and hessian of the problem. Finding closed-form expressions of these derivatives is a major blocking point in creating more versatile inverse form-finding workflows.
Using this insight, an inverse form-finding workflow is built and applied with a closest-fit optimization objective. In funicular structures, this dissertation first focuses on a closest-fit to target surface optimization, giving closed-form formulations of gradients and hessian of the problem. Finding closed-form expressions of these derivatives is a major blocking point in creating more versatile inverse form-finding workflows.

This process optimizer is then reimplemented in an Automatic Differentiation framework, to produce an inverse form-finding tool for funicular surfaces with modular design objectives. This is a novel way of implementing such tools, exposing how the design intent can be represented by more complex objects than a target surface.
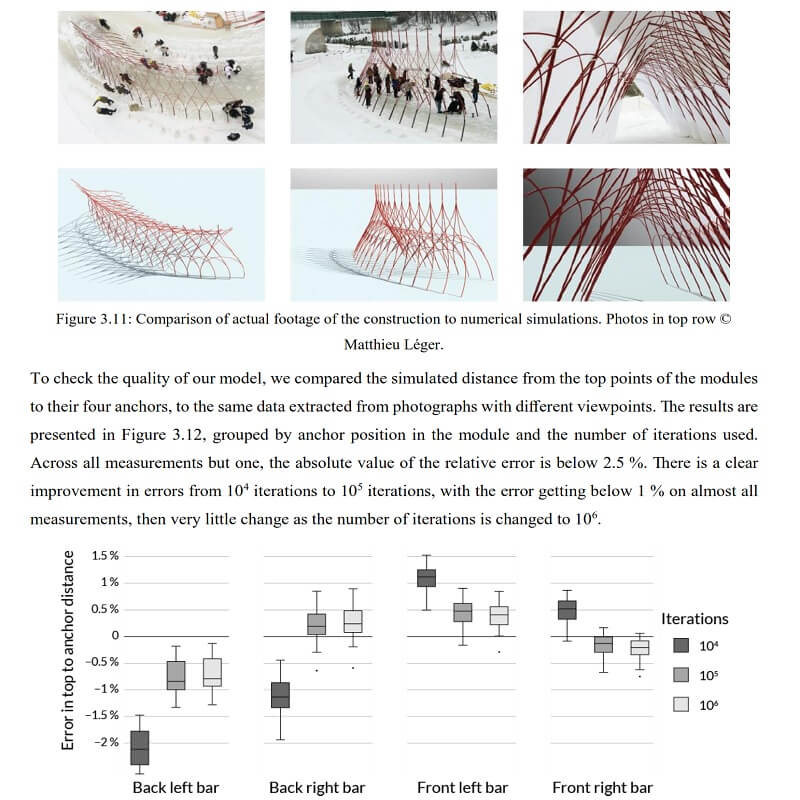 Reproducing existing structures, and generating more efficient funicular shapes for them, the possibilities of the tool are demonstrated in exploring the design space and fine-tuned modifications, thanks to the fine control over the objectives representing the design intent.
Reproducing existing structures, and generating more efficient funicular shapes for them, the possibilities of the tool are demonstrated in exploring the design space and fine-tuned modifications, thanks to the fine control over the objectives representing the design intent.
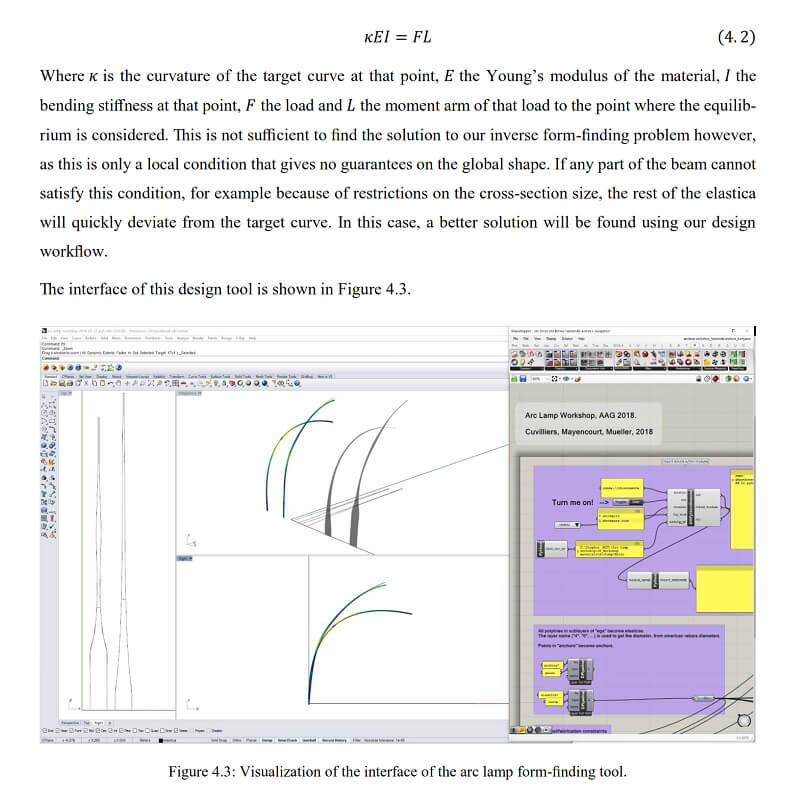

























Comments