Programmable Folding
PROGRAMMABLE FOLDING:
COMPUTATIONAL GEOMETRY WITH EMBEDDED ASSEMBLY LOGIC
Annie Locke Scherer
ITECH M.Sc. Programme
ICD, Institute for Computational Design
ITKE, Institute for Building Structures and Structural Design
2014-2015

One does not normally design leftover waste material. More commonly, one designs and what is left over is discarded. Programmable Folding is centered around strategic cuts. Careful design of removed material has the ability to imbue a flat sheet with intrinsic curvature.
 The aim of this thesis by Annie Locke Scherer, is to create parametrically-derived folding patterns that approximate irregular, doubly-curved surfaces when assembled. Looking at fundamentals of cut patterns, this thesis investigates the relatively unexplored world of origami’s lesser-known cousin: kirigami. This, like origami, is the art of folding sheets but also utilizes simple cuts to program inherent curvature into a flat material.
The aim of this thesis by Annie Locke Scherer, is to create parametrically-derived folding patterns that approximate irregular, doubly-curved surfaces when assembled. Looking at fundamentals of cut patterns, this thesis investigates the relatively unexplored world of origami’s lesser-known cousin: kirigami. This, like origami, is the art of folding sheets but also utilizes simple cuts to program inherent curvature into a flat material.
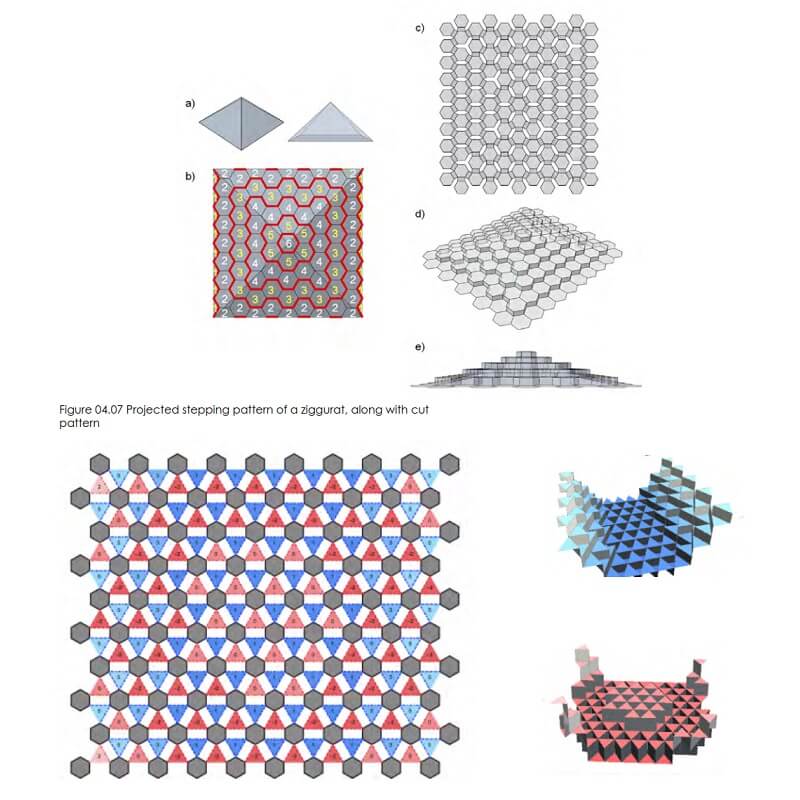 Programmable Folding analyzes the basic geometrical rules of kirigami folding, identifying which parameters are flexible and which ones must be followed. The resulting geometrical pattern encodes a sheet material with an inherent assembly logic and provides the necessary information to fold the material into a complex, 3-dimensional surface.
Programmable Folding analyzes the basic geometrical rules of kirigami folding, identifying which parameters are flexible and which ones must be followed. The resulting geometrical pattern encodes a sheet material with an inherent assembly logic and provides the necessary information to fold the material into a complex, 3-dimensional surface.
 This project builds upon research from much of the origami world, particularly referencing the work of Tomohiro Tachi (University of Tokyo), Daniel Piker (Foster + Partners), and Toen Castle (University of Pennsylvania).
This project builds upon research from much of the origami world, particularly referencing the work of Tomohiro Tachi (University of Tokyo), Daniel Piker (Foster + Partners), and Toen Castle (University of Pennsylvania).
 Grasshopper and Kangaroo for Rhino are the primary design tools to realize the geometrical complexities within double-curvature folding. These tools allow for easy manipulation of areas and degrees of curvature, quick generation of a cut and tabbing pattern, and simulation of the final folded geometry.
Grasshopper and Kangaroo for Rhino are the primary design tools to realize the geometrical complexities within double-curvature folding. These tools allow for easy manipulation of areas and degrees of curvature, quick generation of a cut and tabbing pattern, and simulation of the final folded geometry.
 Programmable Folding explores design possibilities of geometry on multiple levels and delivers a final product whose design is embedded in the generated folding pattern. This thesis simplifies complex geometrical problems of approximating an irregular surface, while simultaneously investigating typology, assembly logic and structural performance.
Programmable Folding explores design possibilities of geometry on multiple levels and delivers a final product whose design is embedded in the generated folding pattern. This thesis simplifies complex geometrical problems of approximating an irregular surface, while simultaneously investigating typology, assembly logic and structural performance.

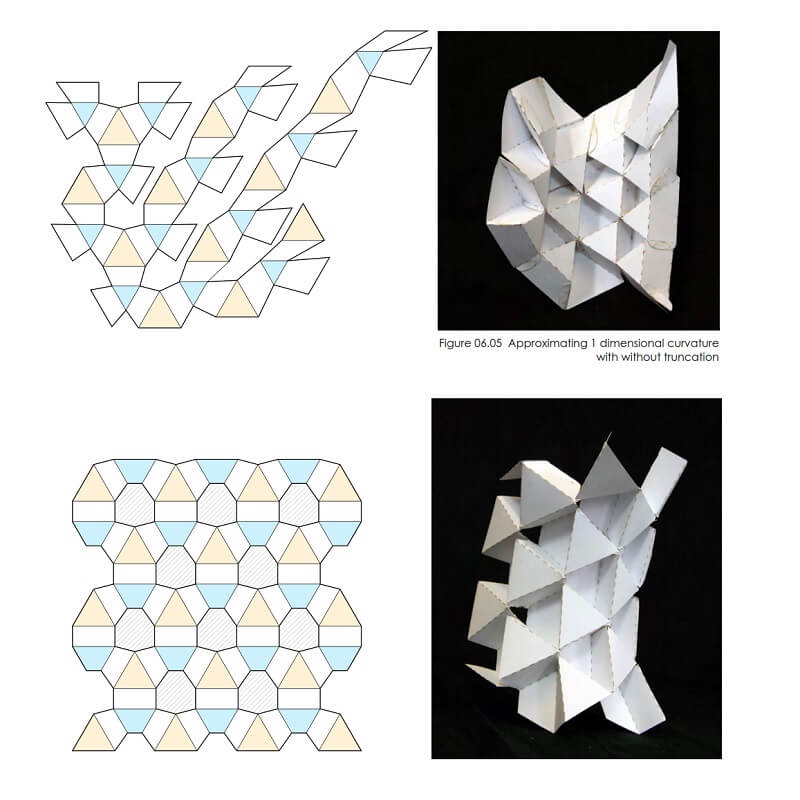





























Comments
VanessaSabrina
Hi, did you use KUKA and Robots in Grasshopper to fabricate ? How is KUKA to be programmed an with which software ? Many regards Vanessa
VanessaSabrina
and
VanessaSabrina
Hi, did you use KUKA and Robots in Grasshopper to fabricate ? How is KUKA to be programmed and with which software ? Many regards Vanessa