Bendable Bracelet
For the most part, laser cut objects consist of flat panels that are either cut or etched before being assembled into a final configuration. There is another way to use laser cutting to create 3D objects from flat materials, and it uses a clever design element called a Lattice or Living Hinge. It is more common to see makers and hobbyists using Living Hinges in laser cut wood, because the properties of this material allow for a significant degree of flex before the material fractures. There are also examples of Living Hinges successfully being implemented in acrylic enclosures, which demonstrates the versatility of this technique – because without using heat to assist bending, acrylic tends to be notoriously brittle.
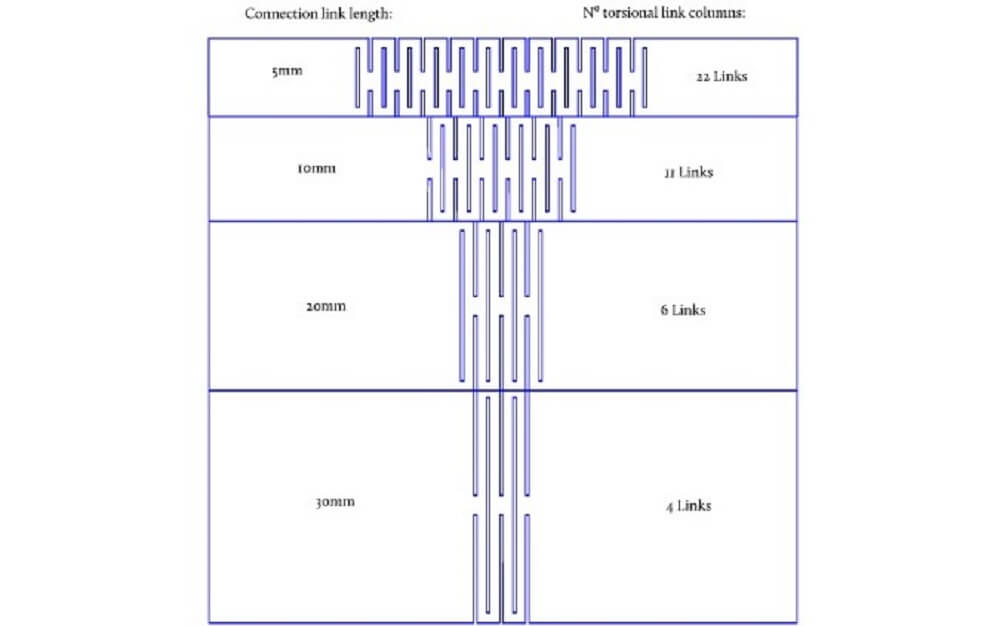
 Living hinges work by exploiting the natural tendency for materials to flex around an array of cuts or notches. As we will see, it is possible to achieve this effect with quite a diverse visual impact; as the core concept of strategically placed cuts can still be achieved using many design variations. In the following test cuts by Martin Breuer, different patterns were evaluated for their pliability and strength across several criteria.
Living hinges work by exploiting the natural tendency for materials to flex around an array of cuts or notches. As we will see, it is possible to achieve this effect with quite a diverse visual impact; as the core concept of strategically placed cuts can still be achieved using many design variations. In the following test cuts by Martin Breuer, different patterns were evaluated for their pliability and strength across several criteria.

Experiments and trial-and-error are one thing, but wrapping your head around the numbers behind what’s actually physically happening to the material gives you an insight into what to expect from your outcomes. While many makers have generously dedicated time to explain the mysteries of the living hinge, the efforts of the Open Source Engineering Hub at Deferred Procrastination go further than most.
In addition to the optimisation of living hinge design for static objects, an added bonus of the mathematical approach is that it opens up the possibility for hinges to be designed for use in moving parts as well.

The key is understanding how to manage the torsional yield stress of the material, which means each of the spring connections will move enough to return to its original shape without permanent deformation.
This can be calculated quite precisely; so long as the following nomenclature doesn’t scare you away:
– Torque (Nm)
– Connected length (m)
– Torsional Modulus of the material (Pa)
– Polar Moment of Inertia for non-circular sections (m4)
– Torsional Stress (Pa)
– material thickness (m)
– number of links in series
– angle of twist (radians)
– total bend angle of the piece
























Comments