Optimization for Digital Fabrication
Optimization-Based and Distributed Control
for Digital Fabrication
Yvonne Rebecca Stürz
A thesis submitted to attain the degree of
DOCTOR OF SCIENCES of ETH ZURICH
2019

In the past years technological advances and the availability of inexpensive hardware with sensing, communication and computational capacities have favored a trend of digitization and automation in many industries. The fields of architecture, construction and civil engineering, however, have hardly been affected by this trend so far. Challenging operating conditions and complex tasks are key factors why the advances in automation are not transferable to construction.
 The emerging field of digital fabrication aims at introducing more efficient building processes, and enabling completely new methods in design and architecture by leveraging tools from digital design and computation, robotic fabrication and automation. This thesis by Yvonne Rebecca Stürz, deals with two main aspects of digital fabrication: Firstly, the automation of complex construction tasks through efficient distributed control of multi-robot systems, and secondly, a completely new building process for lightweight construction, enabled by the form control of a cable net based formwork.
The emerging field of digital fabrication aims at introducing more efficient building processes, and enabling completely new methods in design and architecture by leveraging tools from digital design and computation, robotic fabrication and automation. This thesis by Yvonne Rebecca Stürz, deals with two main aspects of digital fabrication: Firstly, the automation of complex construction tasks through efficient distributed control of multi-robot systems, and secondly, a completely new building process for lightweight construction, enabled by the form control of a cable net based formwork.
 Interconnected systems, such as cooperating multi-agent systems, have a great potential of performing highly complex tasks. In the first part of this thesis, contributions towards efficient scalable distributed control design for heterogeneous interconnected systems are presented. Based on a linear fractional representation of the system with a decentralized part and an interconnection part, the full block S-procedure is applied for controller synthesis.
Interconnected systems, such as cooperating multi-agent systems, have a great potential of performing highly complex tasks. In the first part of this thesis, contributions towards efficient scalable distributed control design for heterogeneous interconnected systems are presented. Based on a linear fractional representation of the system with a decentralized part and an interconnection part, the full block S-procedure is applied for controller synthesis.
 For scalability of the design, author introduces structural constraints on the Lyapunov and multiplier matrices, which allows us to decompose the matrix inequalities into smaller ones of the order of the individual subsystems. Furthermore, a distributed solution method of the resulting coupled synthesis equations based on the Alternating Direction Method of Multipliers is proposed. The design only requires nearest-neighbor communication and no central coordination.
For scalability of the design, author introduces structural constraints on the Lyapunov and multiplier matrices, which allows us to decompose the matrix inequalities into smaller ones of the order of the individual subsystems. Furthermore, a distributed solution method of the resulting coupled synthesis equations based on the Alternating Direction Method of Multipliers is proposed. The design only requires nearest-neighbor communication and no central coordination.
 The proposed methods are applicable to general heterogeneous systems, and the communication topology of the controller is a design choice. By introducing a new system classification consisting of multiple groups of homogeneous subsystems and different interconnection types, a more compact controller synthesis is derived with improved computational scalability. In order to improve the control performance given a communication topology, the interconnected controller design methods are applied to an augmented state space representation of the system.
The proposed methods are applicable to general heterogeneous systems, and the communication topology of the controller is a design choice. By introducing a new system classification consisting of multiple groups of homogeneous subsystems and different interconnection types, a more compact controller synthesis is derived with improved computational scalability. In order to improve the control performance given a communication topology, the interconnected controller design methods are applied to an augmented state space representation of the system.
 The individual augmented subsystem models contain copies of states of neighboring subsystems, which provides them with model information about their couplings. This is particularly beneficial if the number of communication links is to be minimized. Moreover, author presents efficient methods for the design of minimum communication topologies to eliminate all so-called fixed modes, which would prevent the system from being stabilizable, or limit its performance, if not removed.
The individual augmented subsystem models contain copies of states of neighboring subsystems, which provides them with model information about their couplings. This is particularly beneficial if the number of communication links is to be minimized. Moreover, author presents efficient methods for the design of minimum communication topologies to eliminate all so-called fixed modes, which would prevent the system from being stabilizable, or limit its performance, if not removed.
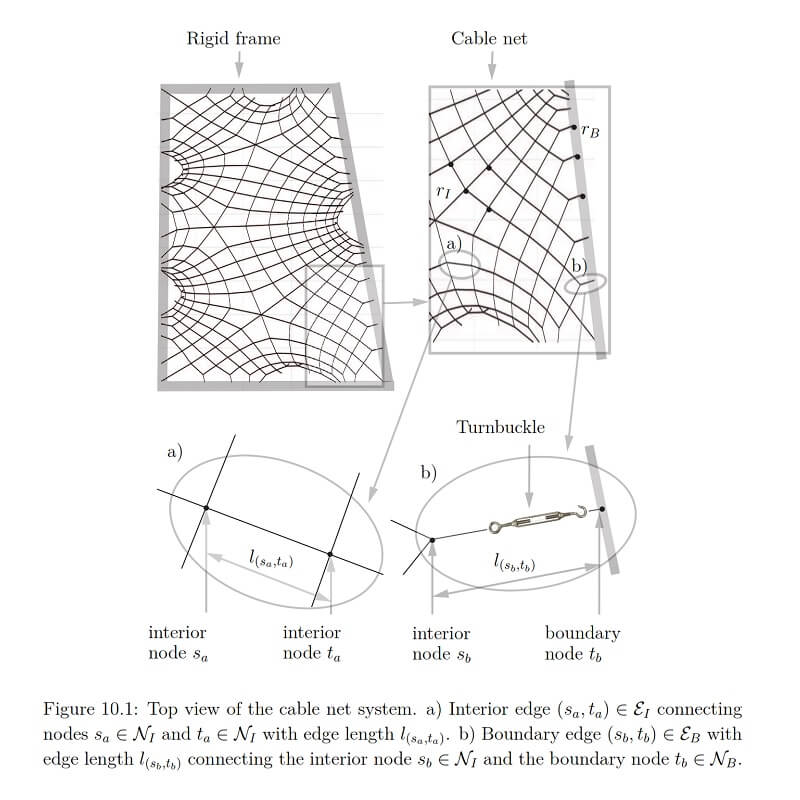
 The second part of this thesis introduces a novel control application, where feedback- based optimal control is introduced into the construction process. Tensioned cable nets can be used as a component of lightweight flexible formwork for the construction of thin concrete architectural shells. However, meeting the structural and mechanical specifications of such shells requires precise positioning of the nodes of the cable net to precisely achieve the designed and optimized form.
The second part of this thesis introduces a novel control application, where feedback- based optimal control is introduced into the construction process. Tensioned cable nets can be used as a component of lightweight flexible formwork for the construction of thin concrete architectural shells. However, meeting the structural and mechanical specifications of such shells requires precise positioning of the nodes of the cable net to precisely achieve the designed and optimized form.
 Therefore, the goal of the proposed control method is to minimize the deviations of the tensioned cable net from the target form in the presence of fabrication tolerances and model uncertainties. The form control is crucial for enabling the use of this efficient lightweight formwork. It is based on measurements of the nodal positions of the cable net and possible actuation of the boundary cable lengths. Because taking measurements and making cable lengths adjustments is time-consuming on the construction site, a two-step algorithm is proposed which exploits model know- ledge and measurement data.
Therefore, the goal of the proposed control method is to minimize the deviations of the tensioned cable net from the target form in the presence of fabrication tolerances and model uncertainties. The form control is crucial for enabling the use of this efficient lightweight formwork. It is based on measurements of the nodal positions of the cable net and possible actuation of the boundary cable lengths. Because taking measurements and making cable lengths adjustments is time-consuming on the construction site, a two-step algorithm is proposed which exploits model know- ledge and measurement data.
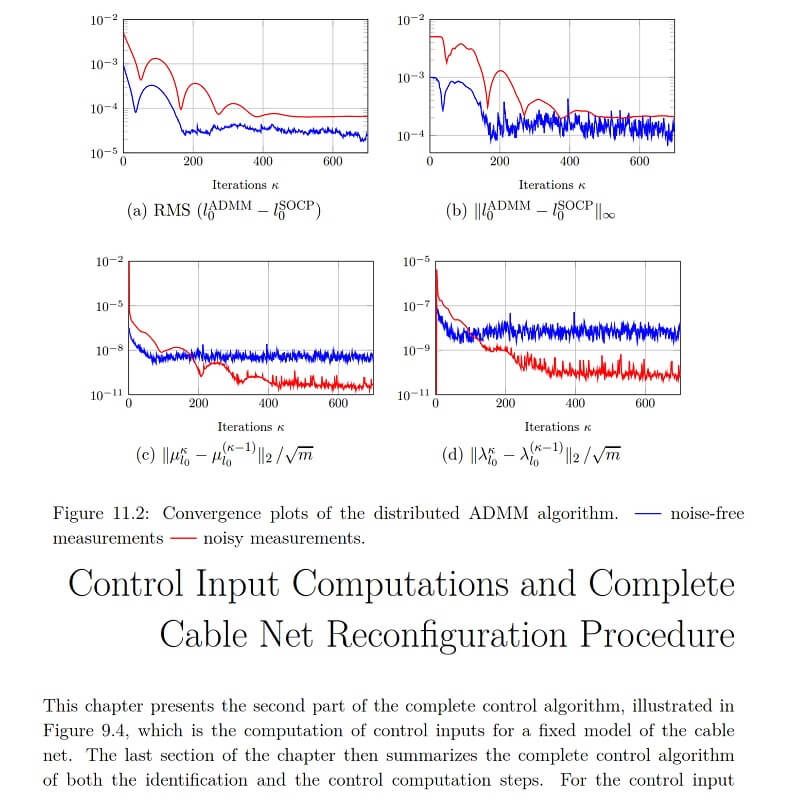
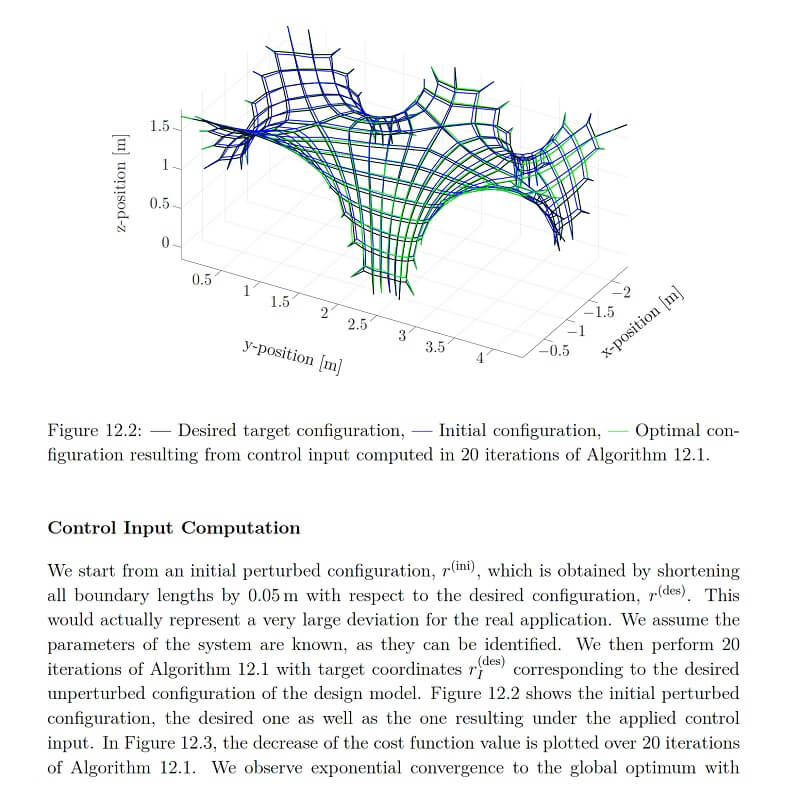
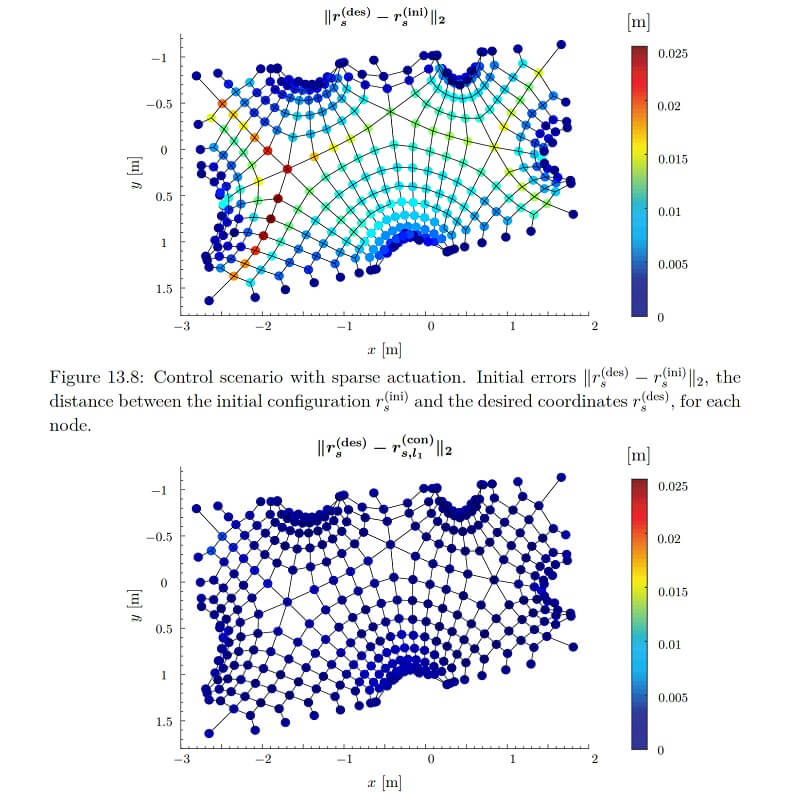
 In each control iteration, first, the measurements are used to identify model parameters by a distributed optimization method. Second, for the control input computation, a sequential quadratic programming variant is proposed. For a given identified model, it generates a sequence of feasible iterates for the form optimization problem. The efficient computations involve solving quadratic and second-order cone programs. The algorithm is proved to converge to a Karush-Kuhn-Tucker point of the form optimization problem. A sparsity-promoting optimization-based method is proposed to further reduce the number of cable adjustments. The developed control strategy is experimentally validated on a quarter-scale prototype of a flexible cable net formwork for a doubly-curved roof shell.
In each control iteration, first, the measurements are used to identify model parameters by a distributed optimization method. Second, for the control input computation, a sequential quadratic programming variant is proposed. For a given identified model, it generates a sequence of feasible iterates for the form optimization problem. The efficient computations involve solving quadratic and second-order cone programs. The algorithm is proved to converge to a Karush-Kuhn-Tucker point of the form optimization problem. A sparsity-promoting optimization-based method is proposed to further reduce the number of cable adjustments. The developed control strategy is experimentally validated on a quarter-scale prototype of a flexible cable net formwork for a doubly-curved roof shell.



























Comments