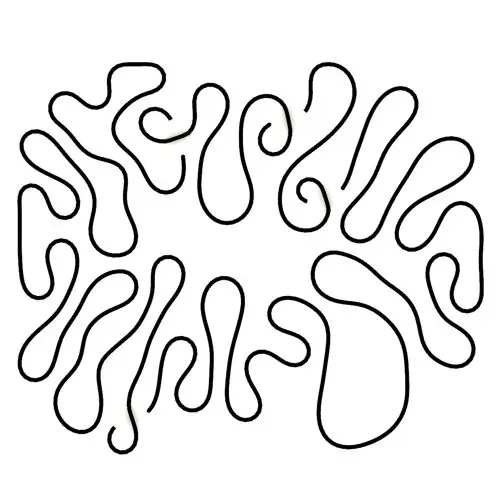
Differential Growth
In this Kangaroo Grasshopper tutorial, you’ll learn how to create a differential growth pattern on any mesh surface by projecting
Branching Fractal
Fractals are intricate patterns or structures that are self-repetitive at every scale, meaning they appear the same or similar regardless of the level of magnification.
Emerging from simple mathematical equations, fractals defy our classical sense of scale and provide a visual representation of infinity.
Their unpredictable and beautiful nature has captivated scientists, mathematicians, and artists alike.
Fractals can be found in nature, such as in the branching of trees, the structure of snowflakes, and the formation of coastlines, while others are products of pure mathematics.
Delving into the world of fractals allows one to appreciate the balance between chaos and order that exists both around and within us.
1- Koch Snowflake Fractal:
The Koch Snowflake is one of the earliest described fractals, named after Helge von Koch. Starting with an equilateral triangle, each side is modified by adding a smaller triangle at its middle, removing its base, and this process is repeated infinitely. With each iteration, the perimeter of the shape increases, pushing the boundaries of our understanding of length, as the snowflake’s perimeter heads towards infinity while its area remains finite.
2- Sierpinski Triangle:
The Sierpinski Triangle is a mesmerizing pattern of endlessly nested triangles. To visualize its formation, start with an equilateral triangle and remove a smaller triangle from its center. This process is repeated for the remaining triangles, and so on, indefinitely. The resulting fractal showcases a balance between positive and negative space, revealing a pattern that is both intricate and endlessly repeating.
3- Hilbert Curve:
The Hilbert Curve, named after mathematician David Hilbert, is a space-filling curve, meaning it tries to occupy as much of a two-dimensional space as possible without crossing itself. Beginning as a simple U-shaped curve, each iteration involves refining the shape, making it twist and turn more complexly. While it seems to fill up more space with each step, the curve never actually becomes a solid shape, no matter how many times it is iterated.
4- Quadratic Fractal:
Quadratic fractals arise from iterating quadratic functions in the complex plane. One of the most famous examples is the Mandelbrot set. When points from the complex plane are plugged into a simple equation repeatedly, their behavior determines whether they belong to the Mandelbrot set or not. The boundary of this set is where the magic happens: it’s an infinitely intricate fractal that reveals more details no matter how much you zoom in, showcasing the deep complexity that can emerge from simple mathematical rules.
5- Branching Fractal:
Branching fractals are reminiscent of patterns found in nature, like the veins of a leaf or the branching of trees and rivers. Starting with a main ‘trunk’ or line, smaller branches sprout out at certain angles, and from these branches, even smaller branches emerge, and so on. The self-similarity is evident as each smaller branch mimics the pattern of the larger one, creating a visual representation of the recursive processes often found in the natural world.
Video References:
1 _ https://youtu.be/WFtTdf3I6Ug?si=SfGTI6kMQVE3HXwm
2 _ https://youtu.be/40p_YC0yZZQ?si=CdizReVypHUfb-XL
3 _ https://youtu.be/ackDGIKx1cw?si=Wr3Ys2Za5r1Cxixt
4 _ http://datagenetics.com/blog/march22013/index.html
5 _ https://youtu.be/-0ooIpJyCNc?si=yhm74ZR4LdISRM5B
Compilation Video by Zahra Ebrahimi , Mohammad Yazdi
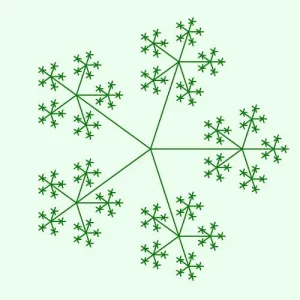
In this Grasshopper example file you can generate a branching fractal tree using the Anemone plugin.
Paracourse Files
Parametric Vase
In this Grasshopper beginner tutorial, you’ll learn how to design a parametric vase with triangular faces, fully controllable height, thickness,
Connecting Towers
In this Grasshopper tutorial, you’ll learn how to design a series of parametric towers arranged around a curve and connect
Difference Contour
In this Grasshopper tutorial, you’ll learn how to design a parametric wall using solid difference and contour techniques.
Parametric Mesh
In this Grasshopper example file, you can model an exoskeleton Mesh structure with entwined curves parametrically.
Voronoi Multipipe
In this Rhino Grasshopper tutorial for beginners, you’ll learn how to model a parametric Voronoi MultiPipe SubD structure on a
Space Frame
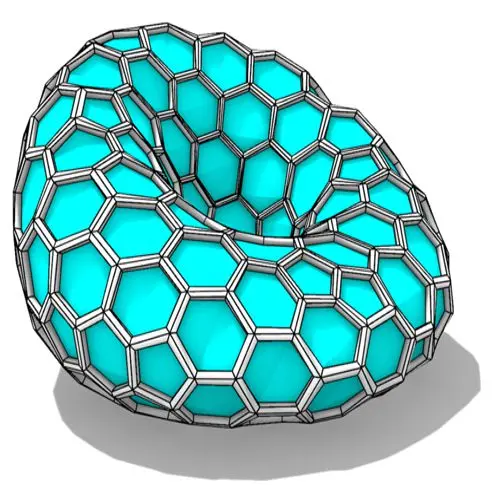
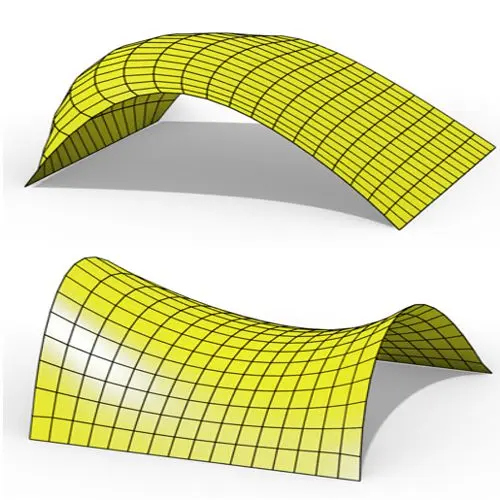
In this Grasshopper tutorial, you’ll learn how to create a simple two-layer Vierendeel space frame structure by defining any four-sided
Voronoi Mesh
In this Grasshopper Voronoi tutorial, you’ll learn how to create a parametric mesh generated from random or controllable Voronoi cells
Inflated Mesh
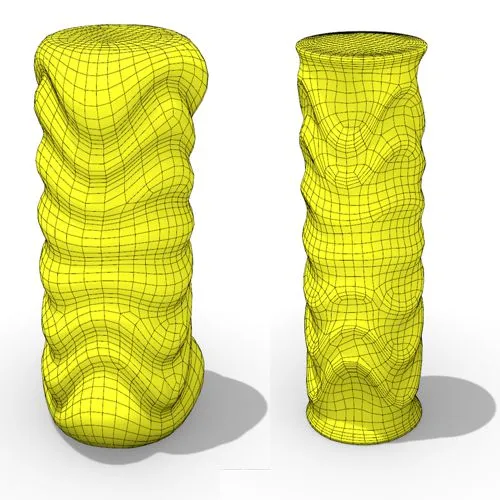
In this Grasshopper tutorial, you’ll learn how to create a dynamic parametric mesh using section curves and Kangaroo physics to
Tensile Structure
In this Grasshopper Kangaroo tutorial, you’ll learn how to model a parametric tensile structure by defining anchor points, the direction
Tensile Structure
In this Grasshopper Kangaroo tutorial, you’ll learn how to model a series of tensile structures arrayed along any open or
Parametric Structure
In this Rhino Grasshopper tutorial, you’ll learn how to model a parametric tree-like structure using only native Grasshopper components, with
Bridge Tower
In this Grasshopper tutorial for beginners, you will learn how to design a parametric tower defined by four control points
Attractor Modules
In this Grasshopper tutorial for beginners, you will learn how to design a parametric facade composed of modular openings.
Frames on Curve
In this Grasshopper tutorial because we know how to convert a series of lines to a frame now we can
Brick Wall
In this Rhino Grasshopper Script, you can model a parametric brick wall by defining a base curve
3- Print + Loop
In this Grasshopper Python Lesson, we are going to talk more about the basics and how to use Print and
Rotating Lines
In this Rhino Grasshopper Tutorial we are going to learn how to make a series of rotating lines around two
6- Parametric Vase
In this Paracourse Lesson (25 Minutes), You can learn how to model a parametric vase by using a Perlin Noise
2- Manage output
In this Grasshopper lesson, I will talk about managing output data with a turning tower example. First I,m going to
2-Canvas
In the introductory lesson, we’ll explore the Grasshopper 1.0 canvas and familiarize ourselves with its fundamental features.
3- Shortest List
Now we have learned the basics of the canvas we will take a look at the most important aspect of
4- Partition List
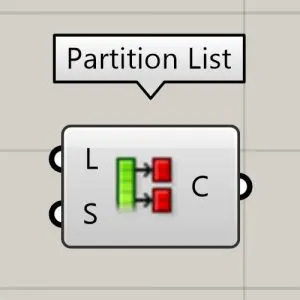
Now we will learn how to manage data with more tools like list length , partition list and simplify.
6- Flatten
After learning about the Partition list, it’s time to learn how to destroy the data trees with flatten and also
Hexagonal Facade
In this Grasshopper example file, you can design a parametric facade with variable-thickness hexagonal cells.
Tensile Facade
In this Grasshopper example file, you can model and simulate a parametric facade with free-form openings using the mesh relaxation
Hexagonal Panels
In this grasshopper example file, you can use a hexagonal module to model a parametric facade.
3D Wave Pattern
In this grasshopper example file, you can use the morph components to apply a 3d wave pattern on a mesh.
Parametric Ideas 327
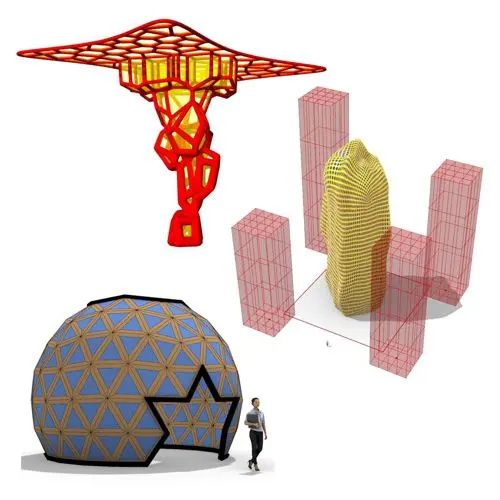
In these Grasshopper example files, you can design a parametric geodesic dome with customizable openings, generate optimized tower forms using
Parametric Ideas 326
In this Grasshopper example file, you can create relaxing Voronoi cells on a facade , a blobby form with a
Reviews
There are no reviews yet.